永磁同步風力發電系統滑模變結構矢量組合控制

張志剛 ，張桂香

(1. 長沙學院 電子與通信工程系, 湖南 長沙，410003；2. 湖南大學 機械與運載工程學院，湖南 長沙，410082)

電力電子技術和永磁同步電機(Permanent magnet synchronous generator, PMSG)制造技術的發展[1-3]為風力發電設備的有效控制提供了有力的技術保障。但在變速恒頻風力發電技術中，由于省略齒輪箱以及發電機與電網之間沒有直接耦合功能，故永磁同步風力發電機的直驅系統具有能量損失少、維護成本低、抗電網波動能力強、可靠性高等優點[4-9]，從而成為變速恒頻風力發電最具發展潛力的主流技術之一[10]。在永磁同步風力發電直驅系統中，永磁同步風力發電機若采用面裝式和多級外轉子結構，往往存在速度傳感器安裝困難以及運轉干擾等問題。即使在能安裝速度傳感器的永磁同步風力發電直驅系統中，速度傳感器也會增加永磁同步電機與控制系統的連接和接口電路，并易受外部環境干擾，并可較大程度地降低永磁同步風力發電直驅系統的可靠性。為解決此難題，多采用無速度傳感器技術解決永磁同步風力發電直驅系統中的永磁同步電機的控制。在相關的永磁同步電機無速度傳感器控制技術研究中，江俊等[11]采用擴展的卡爾曼濾波方法使得永磁同步電機具有優化和自適應能力，而且能很好地抑制測量和擾動噪聲，系統魯棒性較強，但卡爾曼濾波算法復雜，工程實現較為困難；Eskola等[12-13]采用高、低頻信號注入的方法，使得不依賴于永磁同步電機參數進行估計，對參數變化不敏感，具有較強的穩定性。但在永磁同步風力發電直驅系統中，變流裝置的開關頻率較低和注入信號產生的轉矩脈動，同樣使得此方法不易應用于永磁同步風力發電直驅系統中。針對永磁同步風力發電直驅系統運行環境及電機的高磁鏈、多極等特點[14-15]，本文作者提出一種采用滑模結構觀測器觀測無速度傳感器控制算法觀測角度和速度的無速度傳感器方法。該方法具有更強的魯棒性和準確性，并具有適應復雜多變的風力發電環境的能力，工程實現較為簡單。采用此控制技術方法，構建了直驅系統的永磁同步電機矢量控制系統，并在永磁同步電機全速范圍內進行了實驗分析。

1 永磁同步風力發電機滑模變結構矢量控制方法

1.1 永磁同步風力發電機矢量圖及數學模型

永磁同步風力發電機矢量如圖 1所示。其中：α為功率因數角；J為永磁同步風力發電機轉動慣量，xOy坐標系中y軸以轉子感應電動勢e0定向；XOY坐標系中Y軸以定子電壓矢量us確定方向。

可在xOy坐標系中建立永磁同步風力發電機矢量數學模型。

圖1 PMSG空間矢量圖Fig.1 Space-vector diagram of PMSG

定子相電壓us的x軸分量ux可表示為：

式中：δ為功率角；Rs為定子相電阻；Lx為直軸電感；ix為定子相電流is在xOy坐標系中的x軸分量；p為微分算子；ωs為同步電角速度；Ly為交軸電感；iy為定子相電流is在xOy坐標系中的y軸分量。

定子相電壓us的y軸分量uy可表示為：

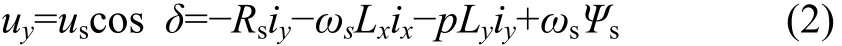
式中：Ψs為電樞合成磁鏈。電磁轉矩Tem可表示為：

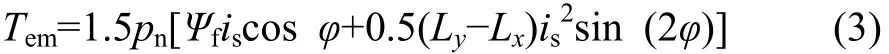
式中：pn為極對數；Ψf為轉子磁鏈；Ψs為電樞合成磁鏈。電磁功率Pem可表示為：

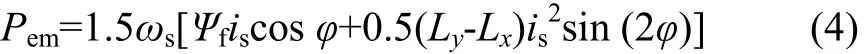
運動方程可表示為：

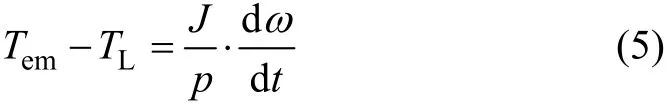
式中：TL為電機負載轉矩。

1.2 滑模變結構矢量控制器設計

取永磁同步風力發電機矢量控制狀態變量為：

式中：ωr為永磁同步風力發電機給定轉速；ωs為永磁同步風力發電機實際轉速。綜合式(1)～(6)可得：

為使永磁同步風力發電機無超調地到達穩定，選擇s為滑模面，則：

設永磁同步風力發電機矢量系統的變指數趨近律為：

式中：ε和α分別為可設定的變指數趨近律參數；sign(s)為開關函數，可定義為：

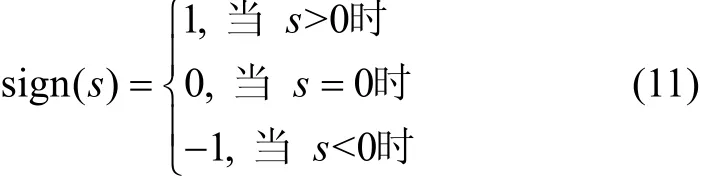
故可得永磁同步風力發電機變指數趨近律的滑模控制器的控制律為：

式(12)表明：永磁同步風力發電機在滑模面以外運動點呈指數方式趨向滑模面運動，當接近滑模面時，永磁同步風力發電機進入切換帶，其穿越滑模面的速度和幅度均隨誤差的絕對值(|z1|=|ωr-ωs|)的減小而減小，理想情況是最終會穩定到原點，誤差為 0，導致抖振的滑模切換項sign(s)消失，抖振消除。為確保永磁同步風力發電機會以較快的速度進入滑模面，并更快地趨近于原點而不會產生大的抖振，通常ε可以設定得比較小，α可以設定較大值。

1.3 永磁同步風力發電機無速度傳感器方法

當以最低切入風速進行發電時，永磁同步風力發電機定子電壓的頻率和幅值一般占額定頻率和幅值的30%以上，且空載時定子相電壓us等同于轉子感應電動勢e0。因此，若采用基于單同步參考坐標系的軟件鎖相環(Single synchronous reference frame software phase locked loop, SSRF-SPLL)模型鎖相us，則空載運行時的轉子磁場位置可實時確定，并且當永磁同步風力發電機帶載運行時，由圖1所示矢量關系以及定子相電壓us與轉子感應電動勢e0間相差角度δ，則可采用SSRF-SPLL模型鎖相的定子電壓矢量角θ作為前饋輸入，根據電機模型和模型參考自適應系統(Model reference adaptive system, MARS)原理獲取δ，便可實現轉子位置的準確定向。

1.3.1 定子相電壓的矢量角值確立

us矢量定向角 θ可通過 SSRF-SPLL模型實時檢測，其基本原理如圖2所示。在圖2中，u1，u2和u3為傳感器檢測的定子三相電壓，一次坐標變換表示三相靜止坐標系到兩相靜止xOy坐標系的變換，二次坐標變換表示xOy坐標系到XOY坐標系的變換。usX和usY為XOY坐標系中的定子電壓分量，ωs為us的同步旋轉角速度。圖2中定子電壓us定向在Y軸上，如圖1所示。

當永磁同步風力發電機定子電壓中含有高次諧波，因圖2模型中存在2個積分環節，故通過適當降低永磁同步風力發電機定子電壓的頻帶，便可對高頻分量起到很強的抑制作用，從而使得SSRF-SPLL模型的魯棒性較強。

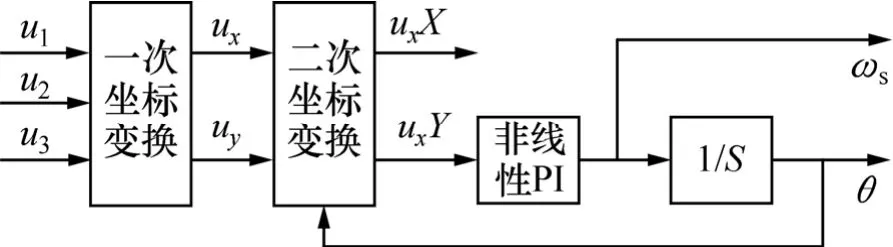
圖2 SSRF-SPLL控制結構原理圖Fig.2 Control structure of SSRF-SPLL

1.3.2 轉子位置定向調節器

通過SSRF-SPLL模型檢測出PMSG的ωs和θ后，δ可通過模型參考自適應控制實時確定。當永磁同步風力發電機穩態發電運行時，式(1)可以轉化為：

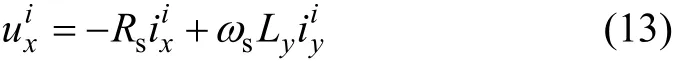
式中：上標“i”表示各參考量序號。

根據式(13)和檢測的θ，便可構建如圖3所示的永磁同步風力發電機轉子位置定向調節器，從而可獲取δ和xOy軸的定向角度θs。圖3中：uy為可調量。通過閉環調節δ，使ux實時跟蹤參考量uxi，從而實現δ和θs的模型參考自適應控制。

圖3 永磁同步風力發電機轉子位置定向控制器Fig.3 Controller of rotor position orientation for permanent magnet synchronous wind power generator

2 永磁同步風力發電系統滑模變結構矢量控制實現

2.1 非線性PI控制器

在傳統 PI控制器的基礎上加入了無記憶的補償控制項。利用系統參考輸入r(t)和輸出y(t)的誤差e(t)構成的非線性函數，利用誤差 e(t)構成非線性函數，這種由誤差 e(t)構成的非線性函數有多種選擇，這里給出如下非線性函數形式：

式中，K0為非線性增益系數。

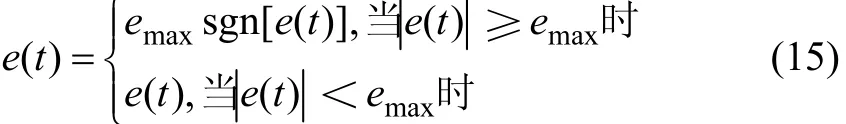
非線性PI控制算式為：

式中：K0為非線性增益系數；Kp為比例增益系數；Ti為積分時間常數。式(6)寫成傳遞函數的形式為：

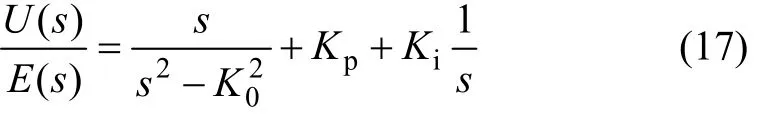
選取較小的采樣周期T0，則：

式中：Δf=Δe(n){exp[K0e(n)]-exp[-K0e(n)]}/2；Δe(n)=e(n)-e(n-1)；Ki=KpT0/Ti。

2.2 永磁同步風力發電系統滑模變結構矢量組合控制仿真

采用Matlab/simunink仿真，電機參數Lx=Ly=9.0 mH，Rs=3.125 Ω，Ψf=0.2 Web，p=4，J=8.5 g·m2。永磁同步風力發電機滑模變結構矢量組合控制系統采用如圖4所示的組合控制策略圖。在該組合控制策略中，速度調節器采用滑模控制策略，電流環采用非線性PI矢量控制，其仿真結果如圖5～7所示。

圖5所示為風速與電角速度變化仿真曲線。從圖5可見：經永磁同步風力發電機滑模變結構矢量組合控制后，每次調整后的穩定電角頻率和理論值相吻合，實現了抗干擾性的組合控制和變速恒頻的特性。而由圖 6所示的角速度滑模控制與組合控制比較可以得知：與傳統的滑模控制控制相比，永磁同步風力發電機滑模變結構矢量組合控制方法更快速。

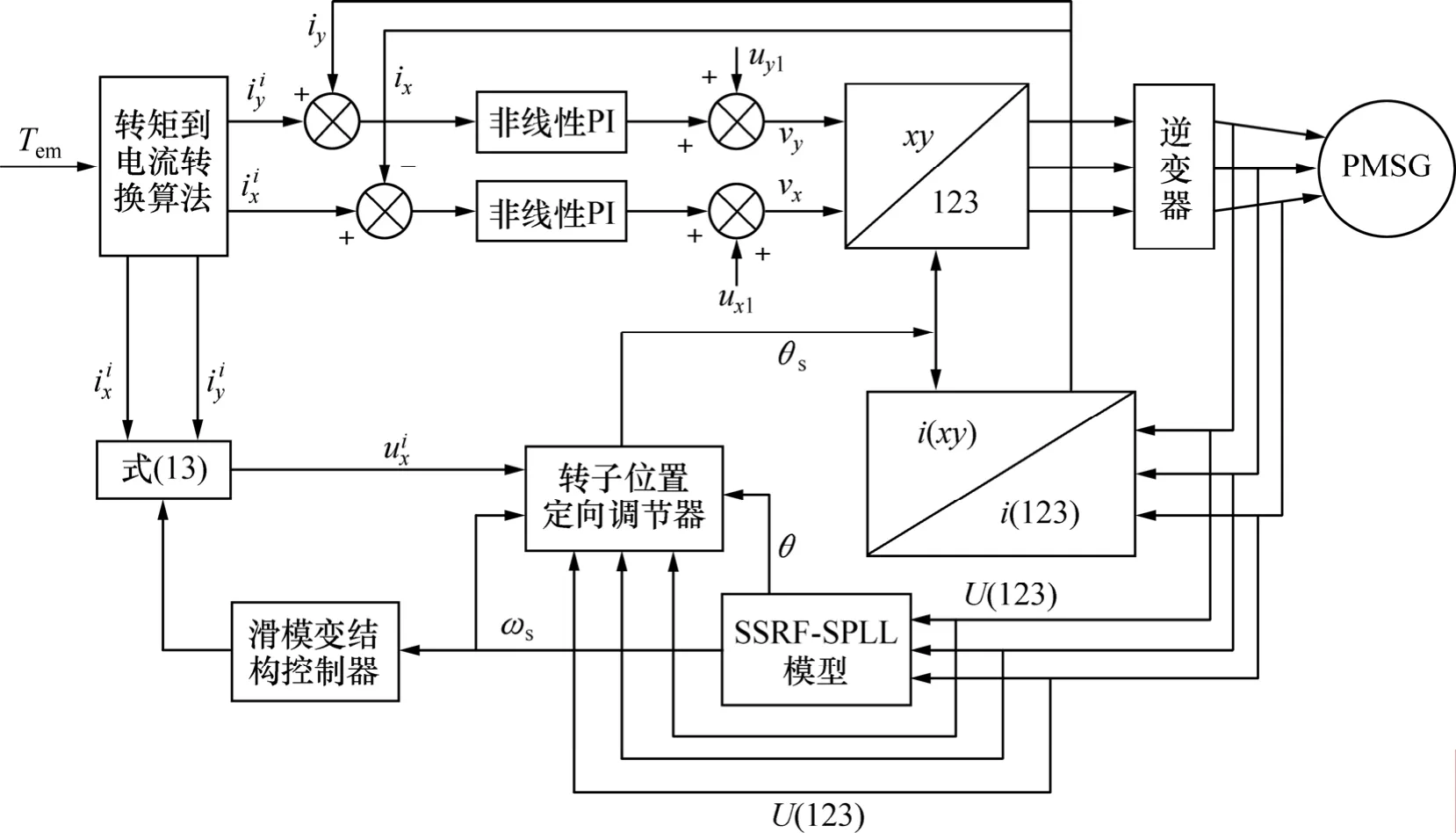
圖4 永磁同步風力發電機滑模變結構矢量組合控制框圖Fig.4 Structure of combined control of sliding mode variable structure vector for permanent magnet synchronous wind power generator

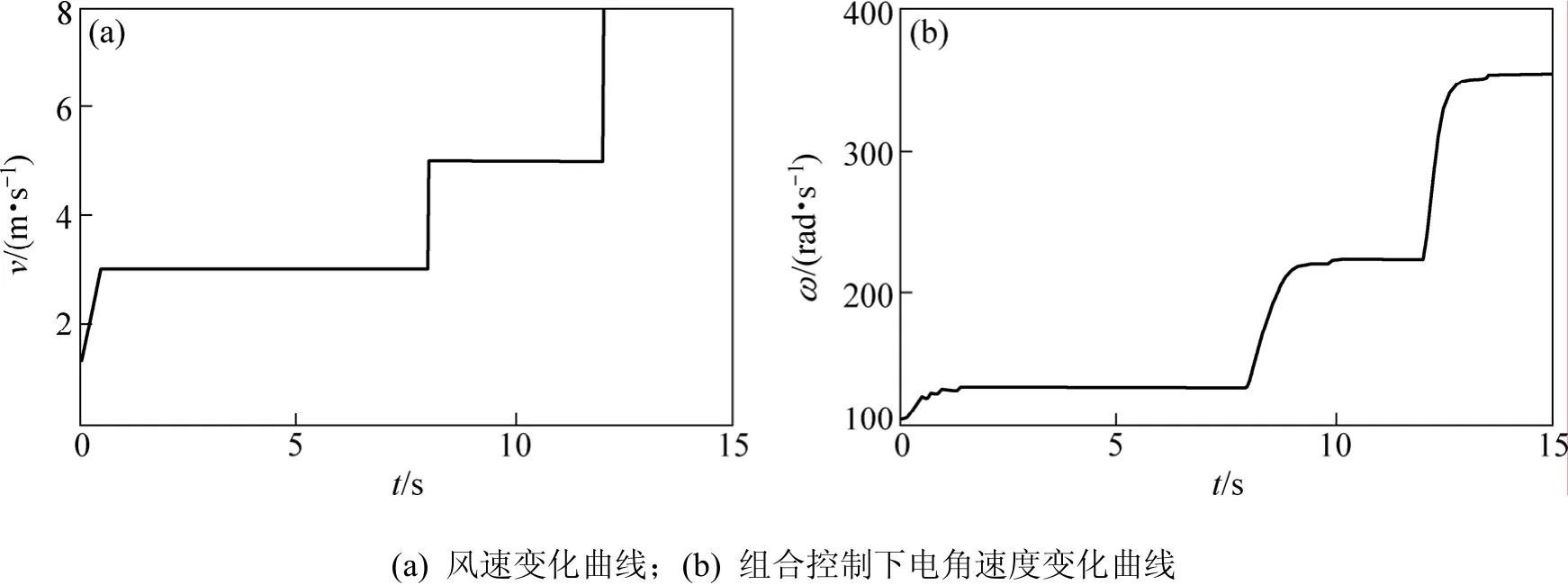
圖5 風速與電角速度變化曲線Fig.5 Wind speed and electrical angle frequency

圖6 角速度滑模控制與組合控制比較圖Fig.6 Comparison of sliding mode control and combined control

圖7 電機轉速波形Fig.7 Waveform of speed response of motor

永磁同步風力發電機轉速波形仿真曲線如圖7所示。從圖7可以看出：采用滑模變結構矢量組合控制的永磁同步電機的轉速上升速率快，在達到穩定值時，無超調量；速度環采用滑模變結構矢量控制的電機轉速響應時間長，有超調量。

在如表1所示的理想情況下加入5%的建模誤差，分別采用本文提出的滑模變結構矢量組合控制方法和文獻[16]控制方法進行控制，可得電角速度時間響應對比結果如圖8所示。

圖 8結果表明，加入 5%的建模誤差對采用文獻[16]控制方法所得到的電角速度時間響應曲線影響較大，而對本文提出的滑模變結構矢量組合控制系統影響較小，說明本文提出的滑模變結構矢量組合控制系統具有較好的魯棒性能。

表1 兆瓦級永磁同步風力發電機參數Table 1 Parameters of PMSG

圖8 電角速度時間響應對比Fig.8 Contrast to electrical angle time respond

3 結論

(1) 針對永磁同步風力發電直驅系統的工程應用，采用基于現代控制理論的滑模觀測無速度傳感器控制算法觀測角度和速度的無速度傳感器方法，并提出速度調節器采用滑模控制策略、電流環采用非線性PI矢量控制的組合控制策略。

(2) 在電機可能運行的速度范圍內，該算法工程實現較簡單，系統魯棒性強，動態響應快，從而驗證了所提控制算法的正確性和可行性。

(3) 加入 5%的建模誤差對本文提出的滑模變結構矢量組合控制系統影響較小，故本文提出的滑模變結構矢量組合控制系統具有較好的魯棒性能。

[1] 廖勇, 楊順昌. 交流勵磁發電機勵磁控制[J]. 中國電機工程學報, 1998, 18(2): 87-90.LIAO Yong, YANG Shun-chang. Excitation control of alternating current excitation generators[J]. Proceedings of the Chinese Society for Electric Engineering, 1998, 18(2): 87-90.

[2] Fernandez L M, Garcia C A, Jurado F. Comparative study on the performance of control systems for doubly fed induction generator wind turbines operating with power regulation[J].Energy, 2008, 33(2): 1438-1452.

[3] Miao Z X, Fan L L. The art modeling and simulation of induction generator in wind generation applications using high-order model[J]. Simulation Modeling Practice and Theory,2008, 16(5): 1239-1253.

[4] 凌禹, 張同莊, 邱雪峰. 直驅式風力發電系統最大風能追蹤策略研究[J]. 電力電子技術, 2007, 41(7): 3-5.LING Yu, ZHANG Tong-zhuang, QIU Xue-feng. Study on maximum power extraction control for directly drived wind power generating system[J]. Power Electronics, 2007, 41(7):3-5.

[5] 劉其輝, 賀益康, 趙仁德. 變速恒頻風力發電系統最大風能追蹤控制[J]. 電力系統自動化, 2003, 7(20): 62-67.LIU Qi-hui, HE Yi-kang, ZHAO Ren-de. The maximumal wind-energy tracking control of available speed constant frequency wind power generation system[J]. Automation of Electric Power Systems, 2003, 7(20): 62-67.

[6] Morren J, Sjoerd H W. Ride through of Wind Turbines with doubly-fed induction generator during a voltage dip[J]. IEEE Transactions on Energy Conversion, 2005, 20(2): 435-441.

[7] 劉其輝. 變速恒頻風力發電系統運行與控制研究[D]. 杭州:浙江大學電氣工程學院, 2005: 48-66.LIU Qi-hui. The investigation of operation and control for a variable-speed constant-frequency wind power generation system[D]. Hangzhou: Zhejiang University. College of Electrical Engineering, 2005: 48-66.

[8] Slotine J E, Li W. Applied non-linear control[M]. Engle-wood Cliffs, NJ: Prentice-Hall, 1991: 226-269.

[9] 鄭雪梅, 馮勇, 鮑晟. 多變量線性模型不確定系統終端滑模分解控制方法[J]. 控制理論與應用, 2004, 21(1): 11-16.ZHENG Xue-mei, FENG Yong, BAO Sheng. Terminal sliding model decomposed control of multivariable linear uncertain systems[J]. Control Theory & Applications, 2004, 21(1): 11-16.

[10] Wu W, Ramsden VS, Crawford T, et al. A low-speed, high-torque,direct-drive permanent magnet generator for wind turbines[C]//IEEE Industry Applications Conf. 2000. 147-154.

[11] 江俊, 沈艷霞, 紀志成. 基于 EKF的永磁同步電機轉子位置和速度估計[J]. 系統仿真學報, 2005(7): 1704-1707.JIANG Jun, SHEN Yan-xia, JI Zhi-cheng. Speed and rotor position estimation for PMSM based on EKF[J]. J System Simulation, 2005(7): 1704-1707.

[12] Eskola M, Tuusa H. Sensorless control of salient pole PMSM using a low-frequency signal injection[C]//2005 European Conference on Power Electronics and Applications. Tampere,Finland, 2005: 106-115.

[13] 秦峰, 賀益康, 賈洪平. 基于轉子位置自檢測復合方法的永磁同步電機無速度傳感器運行研究[J]. 中國電機工程學報,2007, 27(3): 12-17.QIN Feng, HE Yi-kang, JIA Hong-ping. Investigation of the sensorless control for PMSM based on a hybrid rotor position self-sensing approach)[J]. Proc CSEE, 2007, 27(3): 12-17.

[14] Hilmy Awad, Jan Svensson, M J Bollen. Tuning software phase-locked loop for series-connected converters[J]. IEEE Trans on Power Delivery, 2005, 20(1): 300-308.

[15] 湯蘊璆, 史乃. 電機學[M]. 北京: 機械工業出版社, 2011:15-25.TANG Yun-qiu, SHI Nai. Electric machinery[M]. Beijing: China Machine Press, 2011: 15-25.

[16] 汪令祥, 張興, 張崇巍, 等. 兆瓦級永磁同步風力發電機無速度傳感器矢量控制方法研究[J]. 電工電能新技術, 2009, 28(4):19-22, 41.WANG Ling-xiang, ZHANG Xing, ZHANG Chong-wei, et al. A sensorless vector control method for MW level permanent magnet synchronous generator[J]. Advanced Technology of Electrical Engineering and Energy, 2009, 28(4): 19-22, 41.