等離子體目標寬頻電磁散射特性的快速分析

陳明生 孔 勐 時晶晶 吳先良 沙 威

(1.合肥師范學院 物理與電子工程系,安徽 合肥 230601； 2.中國科學技術大學 信息學院，安徽 合肥 230026； 3.香港大學 電機電子工程系，香港)

1. 引 言

實現軍用目標的電磁隱身是一個極其復雜的系統工程，等離子體作為一種全新的隱身技術，具有吸波頻段寬、價格便宜等諸多優點，正受到廣泛關注，對其寬頻電磁散射特性進行計算和分析具有十分重要的理論和工程意義[1]。

目前國內外分析等離子體寬頻散射特性的算法主要為時域有限差分法(FDTD)[2-3]，然由于數值色散性及復雜邊界處理時所產生的誤差，其計算精度難以令人滿意。而用于求解積分方程的矩量法(MOM)雖具有較高的計算精度，在無解析解的情況下常被視為參考解，但作為頻域算法其在分析寬頻響應時需逐點計算，耗費大量的計算機資源。

基于矩量法[4-5]的寬頻分析算法主要為漸近波形估計(AWE)技術，其主要思想為通過獲得表面電流的Taylor級數逼近并轉化為Padé逼近以改善計算精度，最終獲得關于表面電磁流的一種有理逼近。該方法的提出一定程度上突破了矩量法在寬頻分析上的限制，并被廣泛應用于電磁散射問題的求解[6-7]。然而由于Taylor級數系數的獲得首先要計算阻抗矩陣元素的高階導數，這使得其在提高計算效率的同時耗費了較大的計算內存。此外，在分析等離子體等色散媒質時，阻抗矩陣元素高階導數的計算過程也十分復雜。

鑒于以上考慮，我們提出一種新的“Chebyshev-Maehly”模式以代替傳統的“Taylor- Padé”模式用以分析目標的寬頻電磁散射特性。Chebyshev級數逼近在眾多多項式逼近中具有最佳一致逼近性，而Maehly逼近在有理逼近中同樣具有最佳一致逼近性[8]，因此，從理論上保證了所提算法的高精度性。此外，Chebyshev級數的獲得過程無需求解阻抗矩陣元素的高階導數[9]，十分適用于等離子體等色散介質的分析。同時，Chebyshev級數亦可轉化為Maehly逼近形成高精度的有理逼近。通過理論推導和對不同目標的計算分析，探討了等離體頻率和碰撞頻率變化對其后向電磁散射特性的影響，并驗證了所提算法的高精度、高效率等特征。

2. 理 論

2.1 介質目標積分方程及其矩量法解

如圖1所示，設在背景空間參數為ε1和μ1的情況下， 存在某一介質目標，其介電常數和磁導率分別為ε2和μ2，則應用等效原理可得介質體的表面積分方程。

圖1 介質目標示意圖

在分析介質目標電磁散射特性的眾多積分方程中，PMCHWT方程以良好的矩陣性態、抗內諧振以及較高的計算精度等特點而被廣泛應用[10]，其具體形式如下

(1)

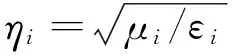
(2)

對于等離子體目標，其相對介電常數和相對磁導率可以用Drude模型[11]分別描述為

(3)

(4)

式中：ωp、ωpm分別為電等離子體和磁等離子體的振蕩頻率；νc、νcm分別為電等離子體和磁等離子體的電子碰撞頻率(一般在1011Hz量級以內)。

應用矩量法，采用Rao-Wilton-Glisson (RWG) 基函數[12]fn(r)(n=1,2,3,…，N)對式(1)中電磁流進行如下形式的展開

(5)

可得矩陣方程

Z(k)I(k)=V(k)

(6)

式中：Z(k)為阻抗矩陣；I(k)為電、磁流系數向量；V(k)為激勵向量。

2.2 寬頻分析的最佳一致逼近理論

對于給定頻帶f∈[fa,fb，]k∈[ka,kb],先作坐標變換，令

(7)

則I(k)在[ka,kb]中的切比雪夫逼近按如下公式給出

(8)

(9)

(10)

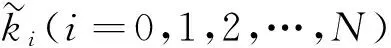
為了進一步提高計算精度， 應用梅利逼近將上述多項式轉化為有理逼近

(11)

式中：b0=1,L+M=N.將式(11)代入式(8)并利用性質

(12)

可以按如下方式解出系數ai(i=0,1,…，L)與bj(j=1,2,…，M)

q=1,2,…，L

(13)

(14)

3. 數值結果

為驗證所提算法的高精度性，首先考慮一個半徑為0.3 cm的均勻介質球體。其相對介電常數為εr=1.5，相對磁導率為μr=1.0.目標表面離散為980個三角單元，在應用矩量法求解PMCHWT方程時生成一個2940×2940維的矩陣方程。分別采用Mie級數進行解析計算、漸近波形估計計算和Chebyshev方法計算，所得結果比較如圖2所示。可以看出：同等階數(相同計算復雜度)情況下，Chebyshev級數(有效計算帶寬為2～30 GHz)的計算精度要遠高于Taylor級數(有效計算帶寬為12～24 GHz)，甚至在沒有轉化為精度更高的有理逼近之前，其有效計算帶寬已超過了Taylor級數轉化為Padé近似(有效計算帶寬為3～26 GHz)的結果。同時由式(8)(9)可以看出Chebyshev方法無需計算電流的高階導數，而漸近波形估計(AWE)技術中為了獲得表面電流的泰勒(Taylor)級數展開，必須求解電流的高階導數，從而需要計算并存儲L+M個阻抗矩陣的導數矩陣，使得內存耗費較矩量法逐點計算成數倍增加。尤其是處理等離子體等色散媒質時，相對介電常數等電磁參數隨頻率變化，其阻抗矩陣的高階導數計算將異常復雜。

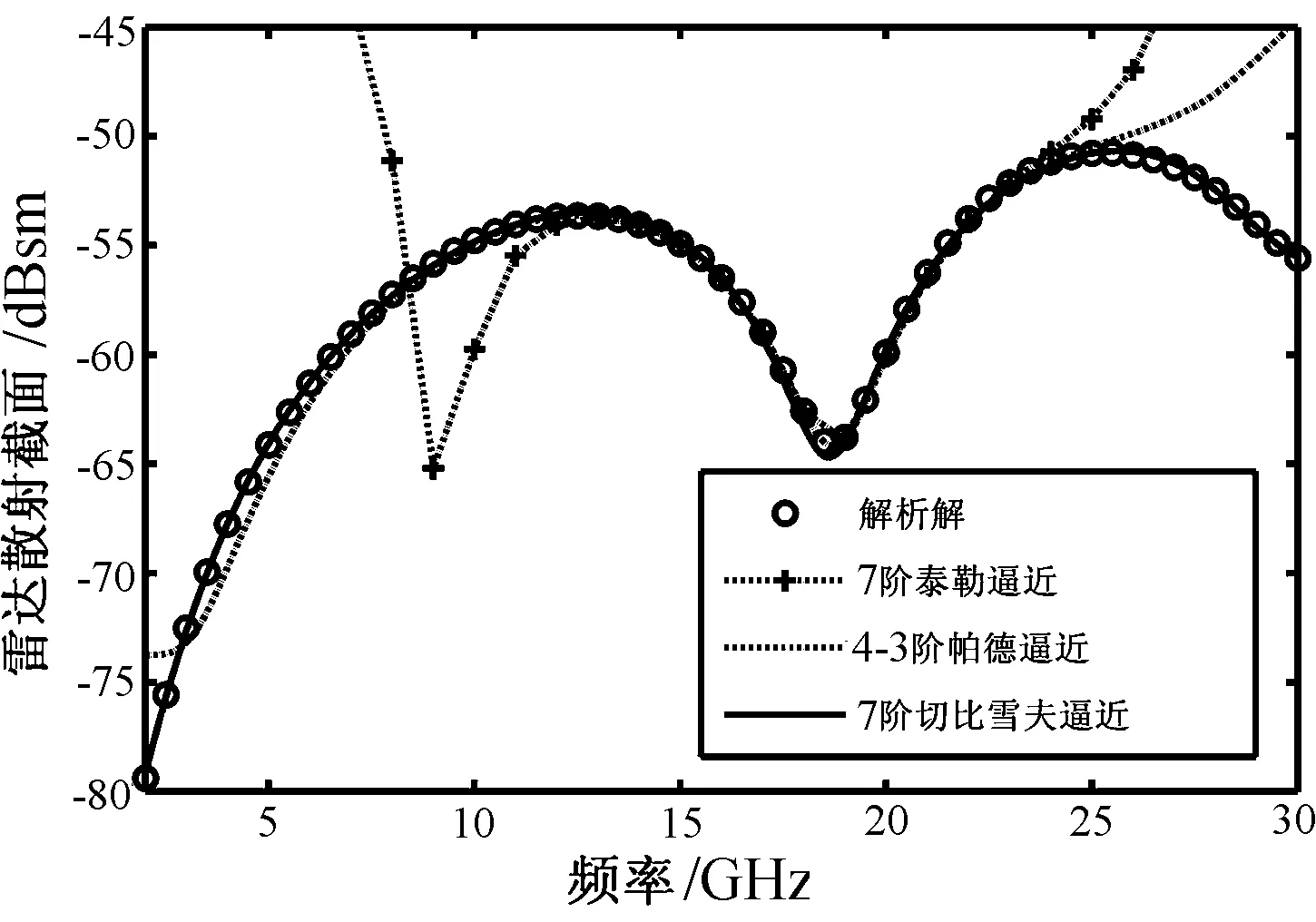
圖2 均勻介質球的RCS頻率響應

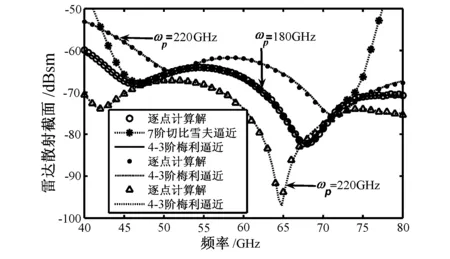
圖3 不同等離子頻率下介質球的RCS頻率響應

如圖3所示：首先，為了驗證Maehly逼近對Chebyshev方法有效計算帶寬的拓展，在等離子頻率為ωp=180 GHz、碰撞頻率為νc=20 GHz下對半徑為0.3 cm的非磁化等離子體目標的寬頻電磁散射特性進行了研究，結果表明：Chebyshev級數轉化為有理逼近后有效計算帶寬得到了進一步拓展。其次，計算了不同等離子體頻率下的雷達散射截面(RCS)寬頻響應，由圖3可以看出：在所研究的頻段，該半徑為0.3 cm等離子體球的后向散射隨等離子體頻率的升高而增強。最后在計算效率方面，以0.5 GHz為步長，采用矩量法逐點計算完成40～80 GHz頻帶的掃頻分析，共耗時4157秒，而Maehly逼近方法以0.1 GHz為步長僅耗時423秒，足見計算效率的提高。而計算過程中并未涉及阻抗矩陣元素求導運算，因此，所提算法更易于程序實現。

為了比較不同碰撞頻率對其后向散射的影響，對上述介質球體，取等離體頻率為ωp=20 GHz，而碰撞頻率分別為νc=0 GHz、νc=40 GHz、νc=80 GHz情況下計算其RCS頻率響應如圖4所示。由此可見：等離子體的碰撞頻率越高，其后向散射越小，隱身特性越好。

圖4 不同碰撞頻率下的RCS頻率響應

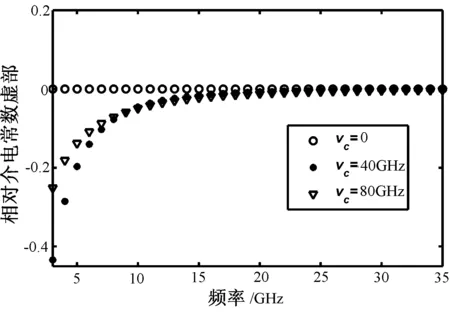
(a) 相對介電常數虛部隨頻率變化

(b) 相對介電常數實部隨頻率變化圖5 相對常數隨頻率變化情況分析

至于20 GHz以后，三種參數下RCS頻率響應幾乎一致，可以歸結為其相對介電常數在20 GHz以后趨于一致，如圖5所示，即實際計算的目標可近似認為是同一目標。

如圖6所示，計算半徑為0.5 cm的磁化等離子體目標的寬頻RCS，其相關參數描述為ωp=120 GHz、ωpm=100 GHz，νc=20 GHz、νcm=10 GHz.當該目標表面離散1280個三角單元時，采用矩量法以1 GHz為步長計算耗時2759秒，而Maehly方法以0.1 GHz為步長計算耗時僅為706秒，兩種方法計算結果在20～50 GHz頻段內吻合良好。

圖6 磁化等離子體球的RCS頻率響應

圖7 均勻介質立方體的RCS頻率響應

為驗證所提算法對不同幾何形態等離子體目標的適用性，對一個1 cm×1 cm×1 cm的立方體等離子體目標進行了計算分析，其相關參數為等離子頻率ωp=20 GHz、碰撞頻率νc=10 GHz.分別采用矩量法逐頻率點求解PMCHWT方程和Maehly方法獲得該目標寬頻電磁響應，其計算結果比較如圖7所示，二者吻合良好。計算時間上，矩量法以0.5 GHz為步長逐點計算耗時4384秒，Maehly近似法以0.1 GHz為步長共耗時679秒。

4. 結 論

針對分析目標寬頻特性的傳統頻域算法在計算精度、內存耗費以及處理色散媒質上的一些弱點，提出了一種基于最佳一致有理逼近的方法，并將該方法應用于等離子體寬頻電磁散射特性的分析。通過數值仿真，得出了一些定性的結論，且驗證了所提算法的高效性：1)與傳統漸近波形估計算法相比，所提算法內存耗費小，且在同等階數情況下有效計算帶寬大為拓展；2)由于無需計算阻抗矩陣元素的高階導數，在處理等離子體一類的色散媒質方面，所提算法簡捷而更易于程序實現。

[1] 莊釗文, 袁乃昌, 莫錦軍, 劉少斌. 軍用目標雷達散射截面預估與測量 [M]. 北京：科學出版社, 2007.

[2] TAFLOVE A and SUSAN C H. Computational electrodynamics: the finite difference time domain method [M]. Boston: Artech House, 2005.

[3] 曾 瑞, 李明之, 周樂柱, 王長清. FDTD 法分析涂覆各向異性材料金屬目標寬帶散射特性[J]. 電波科學學報, 2008, 23(1): 11-16.

ZENG R, LI M Z, ZHOU L Z, and WANG C Q. FDTD analysis of wide2band scatting characteristic of metal target coated by anisotropic medium [J]. Chinese Journal of Radio Science, 2008, 23(1): 11-16.

[4] 楊 卓, 薛正輝, 李偉明. 導體目標瞬態電磁散射的時空矩量法研究[J]. 電波科學學報, 2009, 24(2): 314-317.

YANG Z, XUE Z H, and LI W M. Analyzing frequency selective surface with plane wave approach and the method of moments [J]. Chinese Journal of Radio Science, 2009, 24(2): 314-317.

[5] 任 儀, 聶在平, 趙延文. 基于高階疊層基函數的加速迭代求解方法[J]. 電波科學學報, 2008, 23(1): 100-105.

REN Y, NIE Z P, and ZHAO Y W. An acceleration iterative solution of MoM matrix equation based on higher order hierarchical basis functions [J]. Chinese Journal of Radio Science, 2008, 23(1): 100-105.

[6] SLONE R D, LEE R, and LEE J F. Well-Conditioned Asymptotic Waveform Evaluation for Finite Elements [J]. IEEE Transactions on Antennas and Propagation, 2003, 51(9): 2442-2447.

[7] HANG G B and LI Z F. Novel broadband asymptotic waveform evaluation method and its applications in parameter extraction [J]. International Journal of RF and Microwave Computer-Aided Engineering, 2007, 17(3): 279-285.

[8] 馬振華. 現代應用數學手冊: 計算與數值分析卷[M]. 北京: 清華大學出版社, 2005.

[9] CHEN M S, WU X L, HUANG Z X, and SHA W. Chebyshev approximation for fast frequency- sweep analysis of electromagnetic scattering problem [J]. Chinese Journal of electronics, 2006, 15(4): 736-738.

[10] CHEW W C, TONG M S and HU B. Integral Equations for Electromagnetic and Elastic Waves [M]. New York: Morgan & Claypool Publishers, 2008.

[11] ENGHETA N, ZIOLKOWSKI R W. A positive future for double negative metamaterials [J]. IEEE Transactions on Microwave Theory Technology, 2005, 53 (4): 1535-1556.

[12] RAO S M, WILTON D R, and GLISSON A W. Electromagnetic scattering by surfaces of arbitrary shape [J]. IEEE Transactions on Antennas and Propagation, 1982, 30(3): 409-418.