雙站散射模式響應的分析與應用

李志平

(北京航空航天大學電子信息工程學院，北京 100191)

1. 引 言

矩量法(MoM)由哈林頓(Harrington)首先引入到計算電磁學中求解積分方程[1]，其廣泛應用于天線分析與設計、微波器件模擬和雷達散射截面計算，最大優點是求解精度高。矩量法求解L個入射方向激勵，M個散射方向的雙站RCS時，需要解L次矩陣方程和LM次矩陣向量乘法運算分別獲得表面電流和雙站RCS[8]。雙站特性由于反隱身的需求，日益受到重視，如此循環迭代實際上是無法計算的。為了提高雙站分析的速度，已發展出了幾種方法，如單雙站等效定理[2-3]，以及將物理光學電流作為初始試探解來提高求解速度[4]，前者是近似估計，后者是基于初值近似的循環迭代。為了降低矩量法求解單站RCS的計算復雜度，用基波模激勵展開，不同入射方向激勵起的表面電流是某固定入射方向激勵下的一系列模式表面電流的加權積分[4]。本文將入射和散射的平面波都分解成一系列模式，得出目標雙站RCS與模散射響應成傅立葉變換關系；利用展開模中Bessel函數的性質可闡明模散射響應具有近似成對角分布的稀疏性，根據這些性質和快速傅立葉變換(FFT)，可高效快速實現雙站RCS計算分析和應用。

2. 算 法

任意二維電磁波可分解為橫電波和橫磁波的疊加。根據疊加原理，單獨考慮物體對橫電波和橫磁波的散射即可，為簡單起見，考慮橫磁波的散射。假設目標軸向為z方向，二維理想導體目標所在背景為自由空間，如圖1所示。

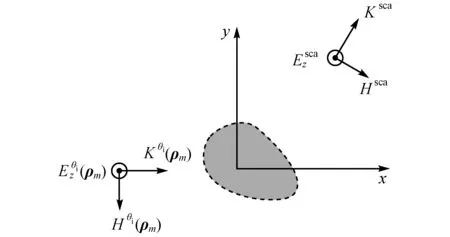
圖1 TM波激勵二維理想導體目標的電磁散射

矩量法求解TM波激勵二維理想導體目標的電磁散射時，將導體橫截面的邊界劃分為N個直線單元，用脈沖基將其上的未知電流密度展開，經檢驗匹配建立電場積分方程的方程組[1]，即

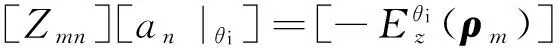
(1)

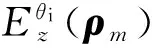
(2)

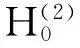
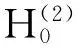
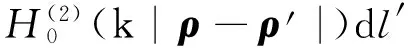
(3)

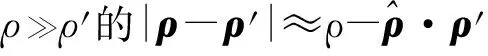
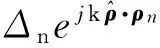
(4)

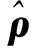
(5)

(6)

求解L個入射方向激勵，M個散射方向的雙站散射，需解L次矩陣方程(1)和LM次矩陣向量乘法(4)運算分別獲得表面電流和雙站散射，即使用共軛梯度迭代求解，計算復雜度也將分別為O(LN2)和O(LMN)。

傍晚，蘇婷婷下班回來，杰克上前擁抱妻子：親愛的，你想死我了！杰克連連在蘇婷婷臉上親吻著，蘇婷婷躲閃著：別這樣，讓爸媽看見了不好。杰克說：爸媽都出去了，看不見的。蘇婷婷放松下來，杰克趁勢把蘇婷婷抱到床上。

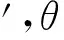
(7)

將式(7)右邊的各階基波模(-j)pJp(kr′)e-jp θ′作為式(1)右邊的激勵，再根據疊加性可將任意方向θi入射激勵起的表面電流表達為基波模表面電流的傅立葉積分。

(9)

其中式(8)確立的線性方程組與入射方向無關，并將求解方程組的次數由L變為2P0+1。而基波模電流重構各個θi入射方向激勵起的電流的式(9)是傅立葉變換。

同樣，將散射到遠區的平面波模式展開，有

(10)

綜合式(10)、(9)和(4)，更換求和次序，并略去常系數項，有

(11)

式(11)是二維(逆)傅立葉變換，其中Tp,q為

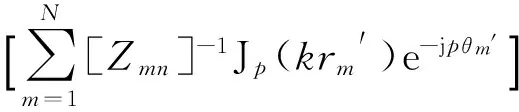
(12)

另外，Bessel函數有性質[6]

J-n(x)=(-1)nJn(x)

(13)

雙站模式散射響應Tp,q在數學上是將p階激勵模在目標空間內經廣義導納矩陣加權后在q階散射模上的投影，在物理上是p階基波模激勵起目標的q階模散射響應，其較大元素集中在對角線附近(p=±q)，遠離對角線時，入射與散射的模式差別增大，二者間的關聯程度將降低，模散射響應將減小，可預估模散射響應近似有沿對角分布的稀疏性。顯然模散射響應是目標的內秉屬性，與入射和散射的觀測角度無關。

3. 仿 真

下面分析波變換中級數截斷的階數對求解精度的影響。平面波展開為Bessel級數和形式，用式(7)左右兩邊的復相關來分析截斷階數P0對級數收斂的影響。

(14)

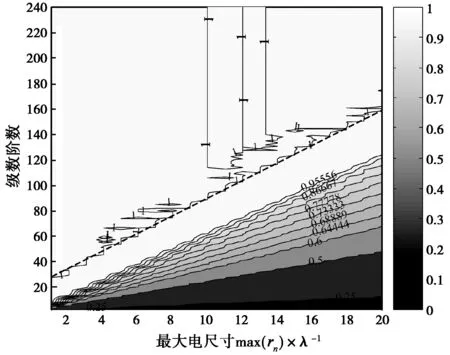
圖2 平面波與其Bessel級數展開的相關系數

由Stratton-Chu積分方程可證明[5]，遠區散射場可表達為與表面電流的積分，即

(15)

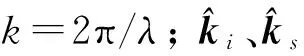
Δθ≤2π/(2×2×2π max(r′)/λ)

(16)

則在2π角度范圍內需要的觀測點數至少為

L=2π/Δθ≥8π max(r′)/λ

(17)

而系數8π大于擬合出的2×6.3，若目標形狀更為復雜，將需更密的間隔來精細地觀測目標的散射特性[7]。

下面計算四個目標的模散射響應和重構雙站散射，并分析忽略遠離對角線的元素對重構的影響，如圖3～6所示。

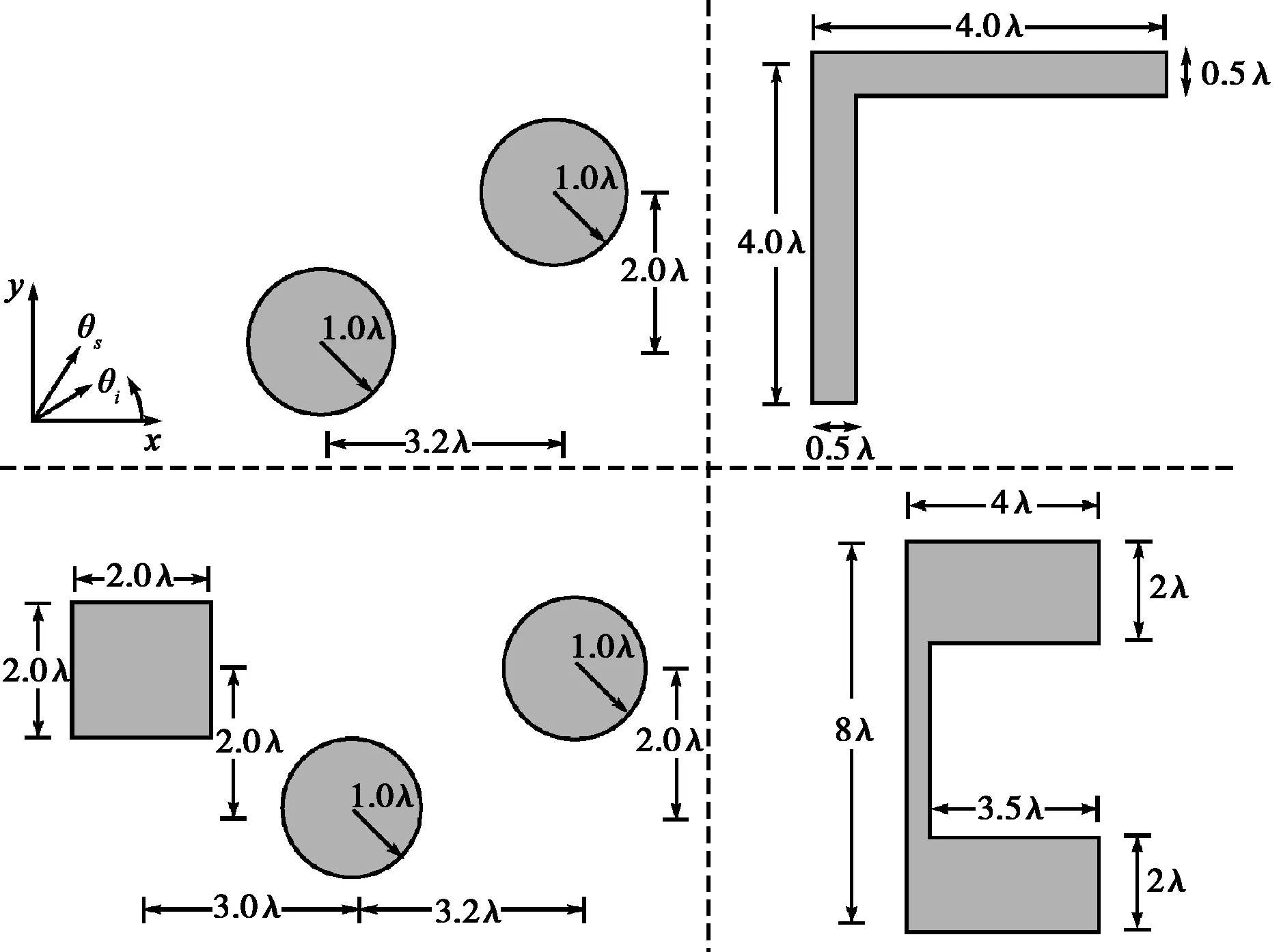
(a) Target I (b) Target II (c) Target III (d) Target IV圖3 仿真的二維目標

為了分析模散射響應的性質，并能體現目標的鏡面散射和多次散射等機制，構造出Target I、II、III和IV如圖3所示，Target I是兩根半徑為1λ的圓柱組合體，兩軸在x和y方向分別相距3.2λ、2λ；Target II是邊長為4λ，邊厚為0.5λ的二面角；Target III是在Target I的基礎上在左上方添了一根寬為2λ的方柱，方柱的軸與Target I左邊圓柱的軸在x、y方向分別相距3λ、2λ；Target IV是底寬8λ，深3.5λ，開口寬4λ，壁高4λ的凹槽。圖4(見411頁)的(a)～(d)分別為四個目標的模散射響應填充等值線圖，橫、縱軸分別為入射和散射的基波模式p、q.

模散射響應有三個特點，其一是“帶限低通”性，對最大尺寸不大于9λ的這三個目標，將模散射響應歸一化于最大值，幅度大于-40 dB的元素都在±40之間的有限帶寬內，難以激勵起足夠強度的高階響應，正如上文分析平面波的模展開式(7)、(10)，截斷的階數取決于電尺寸。其二是“稀疏”性，如圖4所示，幅度大于-10 dB的元素都集中在對角線(p=±q)附近；并且從中可看到經驗性的規律，隨著目標內部耦合現象的加劇，在p=-q附近會集中幅度較強的元素，如圖4(c)中的Target III 比(a)的Target I多了方柱，模響應在p=-q臨近的區域多出現了較強的元素(兩端的位置)，而Target II和IV是強耦合的典型，有著強烈的多次反射，圖4(b)和(d)中在p=-q附近會聚集的更多。其三是“互易對稱”性。

為了分析忽略遠離對角線元素的影響，沿垂直對角線(p=±q)的方向逐漸擴展使用模響應，正負號的選擇由變化較大的方向確定，并與由常規矩量法得到的雙站散射計算相關值。如圖5(見411頁)(a) 和圖6(見411頁)(a)是Target II和IV由常規矩量法計算的雙站散射，而5(b)和6(b)是由全部模響應24.8% 重構所得，相關系數分別大于0.9971和0.9983。圖7是沿垂直對角線(p=±q)的方向擴展時，由占全部模響應的百分比的元素重構計算的和由常規矩量法計算的雙站散射之間的相關系數；當逐漸增加遠離對角線的元素，模響應重構逐漸收斂于矩量法；其中雙劃線、實線、虛線和點劃線分別為計算Target I、II、III和IV相關系數的收斂性曲線，當所占比重約1/4時相關系數都大于0.9970。所以利用這些性質可減少計算時間。

圖7 由模散射響應重構雙站散射的相關收斂曲線

比較兩個都需迭代求解的過程，計算表面電流和模表面電流的次數分別為L和2P0+1，前者正比于8π倍的目標最大電尺寸、后者約正比于14倍的目標最大電尺寸時，平面波的Bessel級數和已很好的收斂，所以根據精度要求可合理減少迭代求解方程的時間。此外，重構使用FFT的開銷較小。

所以，雙站模式響應的這些特征是目標內秉的本質屬性，并且與遠場RCS之間存在傅立葉變換關系，可用來快速計算和識別目標。

4. 結 論

論文基于矩量法來分析目標雙站散射，將入射和散射的平面波都展開為含有基本波函數—Bessel 函數的級數和，得出了目標雙站RCS與模散射響應成傅立葉變換的關系。基于Bessel函數的性質，闡述了模散射響應近似成沿對角分布的稀疏性等性質，并利用稀疏性和FFT快速實現了雙站散射的計算。根據雙站模式散射響應矩陣的性質，仿真計算和比較分析了三個目標，得出由1/8的(收發互易) 散射響應就可重構出高精度的雙站RCS。該方法可推廣到三維和使用快速多極子計算雙站RCS。

[1] HARRINGTON R F. Field computation by moment methods [M]. The MacMillan Company, 1968.

[2] KELL R E. On the derivation of bistatic RCS from monostatic measurements[J]. Proc. IEEE, 1965, 53(8): 983-988.

[3] EIGEL R L, COLLINS P J, TERZUOLI A J, et al. Bistatic scattering characterization of complex objections[J]. IEEE Geoscience and Remote Sensing. 2000, 38(5): 2078-2092.

[4] 王浩剛, 聶在平. 一種求解單站RCS 的高效算法[J]. 電子學報, 1999, (27): 28-31.

WANG Haogang, NIE Zaiping. A highly efficient algorithm for solving monostatic RCS-the method of basic waves exciting[J]. Acta Electronica Sinica, 1999, (27): 28-31. (in Chinese)

[5] STRATTON J A. 電磁理論[M]. 何國瑜,譯. 北京航空學院出版社, 1986.

[6] 梁昆淼. 數學物理方法[M]. 北京: 高等教育出版社, 1960.

[7] 克拉特E F. 雷達散射截面[M]. 阮穎錚, 陳 海, 等譯. 北京: 電子工業出版社, 1988.

[8] 劉紅星, 趙伯琳, 李言榮. FMM算法用于二維復雜散射體的RCS計算[J]. 電波科學學報, 2003, 18(3): 332-336.

LIU Hongxing, ZHAO Bolin, LI Yanrong. Scattering analysis of electrically large 2-D structures with arbitrary cross section using FMM[J]. Chinese Journal of Radio Science, 2003, 18(3): 332-336. (in Chinese)