兩點源角度拖引干擾方法研究

施龍飛 李艷斌 葛 蕾 楊書玲 劉 健

(1.國防科技大學電子科學與工程學院，湖南 長沙 410073； 2.中國電子科技集團第五十四研究所，河北 石家莊 050081)

1. 引 言

隨著單脈沖測角、相控陣等先進雷達技術的發展應用，現代軍用雷達的抗干擾能力越來越強，雷達干擾面臨著更為復雜的困難[1]。

為了擺脫雷達導引頭的角度跟蹤，減輕主動制導導彈對飛行平臺的威脅，拖曳式誘餌等角度欺騙干擾已經廣泛應用于機載雷達對抗裝備中，并在數次實戰中發揮了重要作用。但是這類干擾都是在近距離上、以導彈末制導雷達為對抗對象的[2]。若能夠在中、遠距離上對地基/艦載雷達的跟蹤進行欺騙干擾，則能夠大大提高突防成功率和突防飛機的戰場生存能力。

2. 理論分析

2.1 兩點源角度欺騙干擾

角度欺騙干擾是雷達對抗中廣泛采用的干擾樣式，其主要目的是使雷達角度測量跟蹤系統偏離被保護平臺。角度欺騙干擾的本質是使雷達接收天線口徑面處的目標回波相位波前發生畸變。

兩點源角度欺騙干擾是角度欺騙干擾中應用最為廣泛的一種，廣義的兩點源干擾樣式包括兩類，即相干兩點源干擾(包括交叉眼干擾[2]等)和非相干兩點源干擾(地面反彈干擾、普通拖曳式誘餌等[3])。本文主要考慮采用相干兩點源干擾的方式。

相干兩點源干擾的歸一化角閃爍線偏差可記為[2](歸一化線偏差定義為：兩源視在中心與兩源中心的橫向距離經兩源橫向尺度歸一化后的值[4]，“橫向”指的是在目標中心與雷達接收天線之間連線的垂直平面上的投影，如圖1所示)

(1)

式中： 可將ρ·exp{jρφ}作為到達雷達天線的干擾源2與干擾源1 信號的相對系數； ρ和φρ分別為相對系數的幅度和相位。

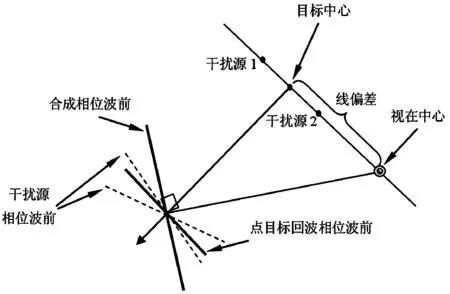
圖1 角度欺騙干擾的作用機理

由式(1)可得，歸一化線偏差e隨相對系數幅度ρ和φρ相位的變化如圖2所示，且

1) 當φρ為180度時，e(絕對值)為峰值點，當φρ接近0度或360度時，e接近于0；

2)ρ越接近于1，線偏差曲線的峰值越大，當ρ=1時，該峰值點趨于無窮大；

3) 參數ρ和1/ρ對應的線偏差曲線以e=0為軸對稱分布，且ρ>1時在該軸的上方，ρ<1時在該軸的下方。

圖2 線偏差隨相對系數幅度和相位的變化

由上面分析，若能夠對兩點源的相對幅度和相對相位進行精確控制，則產生的線偏差值將非常大，從而達到非常好的干擾效果。但由于干擾源1與干擾源2到達雷達天線口面處的路徑是不一樣的，因此兩信號相對相位φρ包括了路程差帶來的相位差φρL和干擾發射源本身的相位差φρS兩部分，即

φρ=φρL+φρS

(2)

由于路程差難以準確獲知，φρL難以獲知，因此，總相位φρ難以控制，從而兩點源干擾很難達到理想的狀態。 交叉眼干擾從機理上巧妙地化解了這一問題：采用轉發干擾方式，干擾源1轉發從干擾源2處接收到的雷達信號，而干擾源2轉發從干擾源1處接收到的雷達信號，因此兩干擾信號的總路程相同、不存在路程差(φρL=0)，干擾機只需對φρS進行控制，理論上能夠實現非常好的角度欺騙效果。

然而，目前來看，交叉眼干擾在實際應用和工程實現上還存在著較大的困難，主要是兩個方面：(1) 實際應用中，由于機載平臺的位置和姿態都是快速動態變化的，從接收到發射的時間內，兩干擾信號的路程差會引起φρL較大的擾動；(2) 工程實現中，由于采樣、數字處理、時鐘同步等原因，兩干擾信號相對相位較難控制。

鑒于上述兩個方面的原因，交叉眼干擾雖然理論上具有非常好的干擾效果，但受硬件系統水平的限制，目前尚未得到大范圍的成功應用。

另一方面，隨著空中作戰平臺向網絡化的方向發展，利用多機編隊實現合成干擾可以解決單機干擾在時間、空間、頻譜上的局限性，特別是對于先進相控陣雷達組網的情況，通過多機雷達對抗系統的密切配合，可有效地消除雷達組網在對抗中的優勢。

本文主要針對雙機編隊角度欺騙干擾，立足于兩源相對相位φρ隨機不可控的情況，研究對相對幅度ρ的控制規則，使角度欺騙干擾能夠達到最佳的干擾效能。

2.2 兩點源角度欺騙干擾參數設計

2.2.1 角度測量偏差統計特性

干擾環境下雷達角度測量偏差的統計特性是兩點源角度欺騙干擾設計的基本依據，文獻[2]在研究擴展目標的角閃爍問題時，提出以均方根和功率譜密度作為主要關注點，雷達設計者依據這兩方面特性對角跟蹤伺服帶寬等進行設計。

與擴展目標角閃爍特性不同，由于兩干擾源相對相位的隨機變化且不相關，因此功率譜密度特性無法使用。另一方面，角偏差對相位很敏感(尤其是當ρ接近于1時，由圖2)，考慮到雷達數據處理中會首先進行剔野再進行角度濾波，因此，本文提出以剔野后的概率密度分布特性作為角度測量偏差的主要特性。

利用式(1)，通過蒙特卡洛仿真并對結果進行統計分析，得到了兩點源干擾造成的角度測量偏差概率密度分布曲線，圖3是不同幅度比ρ下概率密度曲線(雷達與干擾源中心距離為60 km，兩干擾源橫向距離1 km，且對于偏差超過2度的測量值作為野值進行剔除)。由圖3可以看出：

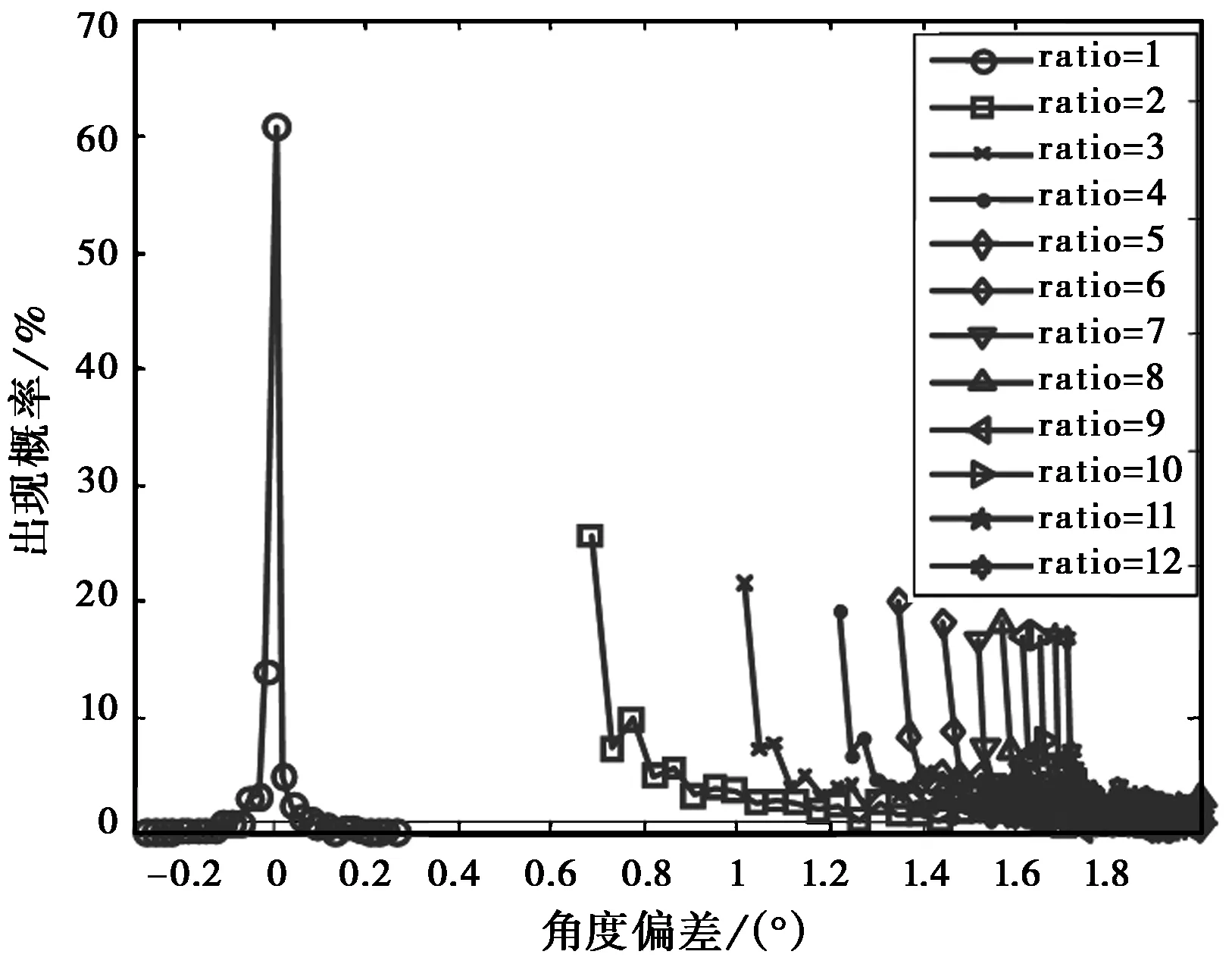
圖3 不同幅度比下測量偏差概率密度分布曲線

1) 不同幅度比情況下，其角度偏差以較大概率聚集于不同區域；

2) 幅度比越大，角度偏差聚集中心(均值)逐漸增大。

圖4是角度偏差均值及其變化斜率，可見：

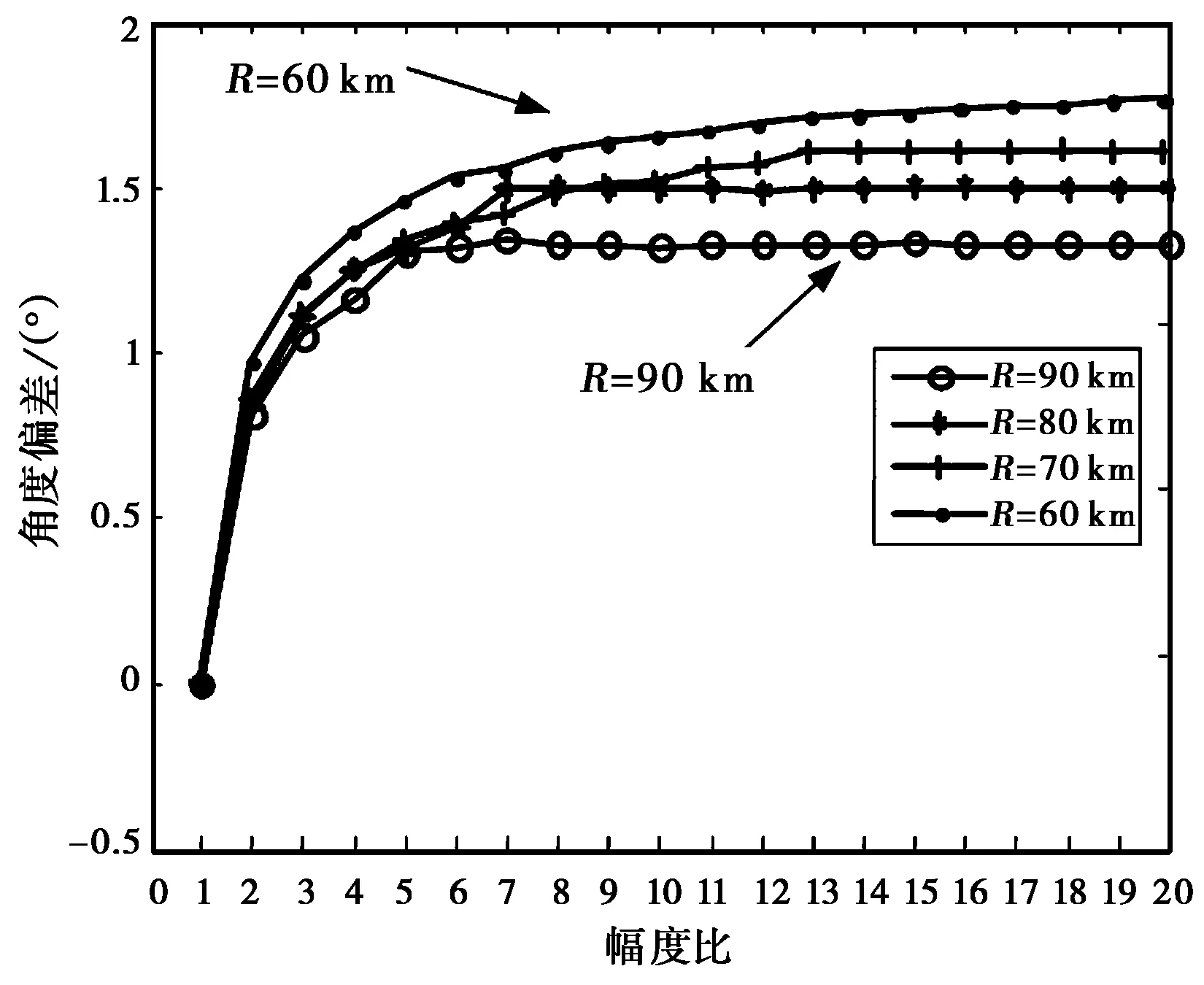
圖4 角度偏差均值

1) 雷達/干擾距離越近，角度偏差均值越大；

2) 隨著幅度比ρ的增大，偏差均值呈增大趨勢，但趨勢變緩；

3) 由圖4可知，偏差均值的變化斜率隨著幅度比增大而迅速下降，當ρ超過某些值之后，斜率接近于0；

2.2.2 雷達角度跟蹤濾波特性分析

雷達通過對目標進行角度測量和平滑濾波實現穩定的角度跟蹤。對于所有的跟蹤濾波算法，一方面要適應測量誤差的起伏以使跟蹤盡量穩定，另一方面也要適應目標運動狀態的變化，這兩方面的要求使得濾波算法在參數設計上只能在兩者之間進行權衡。

以角度跟蹤為例，雷達跟蹤濾波算法可歸結為下面三個核心步驟：

1) 狀態預測

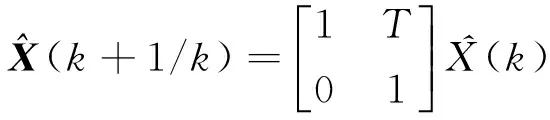
(3)

2) 新息計算

v(k+1)=Z(k+1)-

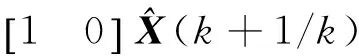
(4)

式中：Z(k+1)為角度測量值； [1 0]為觀測矩陣；v(k+1)稱為第k+1次的新息。

3) 狀態更新

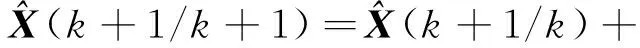
K(k+1)v(k+1)

(5)

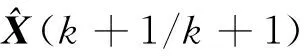
上述三個步驟分別具有不同的作用：

● 狀態預測的主要用途是為雷達跟蹤波束(或天線伺服)提供指向導引；

● 新息V(·)表征了目標運動狀態的變化量；

●增益K(·)是濾波器對目標運動狀態變化的適應度，K(·)越大表示適應能力越強，K(·)越小表示適應能力越弱，但同時其適應測量誤差起伏的能力則越強。

2.2.3 角度拖引干擾設計

2.2.3.1 干擾樣式設計

根據上述分析，本文提出一種新型角度欺騙干擾方式——“角度拖引干擾”,通過有規律地改變兩干擾源幅度比，使雷達角度跟蹤濾波器穩定地朝某一方向偏離，且偏離角度呈增大趨勢，當偏離角度超過某個門限后，關閉干擾源并迫使雷達丟失目標。

在這種方式中，促使雷達丟失目標有兩個方面的原因：一方面，雷達天線波束指向被引導到偏離目標的方向，目標回波接收功率大大降低；另一方面，由于干擾功率比目標回波功率大，雷達自動增益控制(AGC)被調整到低增益的狀態，因此關閉干擾源后目標更難以被檢測到。

2.2.3.2 干擾效能評估標準

角度欺騙干擾的目的是通過對雷達角度測量/跟蹤系統進行干擾，使其跟蹤到錯誤的角度上，并不斷重復“捕獲——跟蹤——丟失——重新捕獲”的過程。

距離波門拖引干擾效能的評估中[5]，通常以“拖引時間”和“失鎖時間”作為評價指標：拖引時間是指從干擾施放到成功迫使雷達丟失目標所需要的時間；失鎖時間指的是雷達從丟失目標到重新捕獲并建立跟蹤所花的時間。

顯然，拖引時間越短、失鎖時間越長，則干擾效果越好。拖引時間決定于拖引速度，而決定失鎖時間的包括雷達本身的搜索性能和拖引程度。本文中，由于主要采用兩點源幅度比控制的實現方法，不能夠達到很大的角度偏差(如圖3)，而對于具有失跟處理能力的先進相控陣雷達(雷達丟失目標后，會在其鄰近區域進行快速補充搜索，該區域一般包括2～3度的區域，很可能會迅速重新捕獲目標)，失鎖時間很可能較短。

綜合上面的分析，本文將拖引時間作為角度欺騙干擾的主要評估指標。

2.2.3.3 干擾參數設計

針對跟蹤濾波器的特性，并利用角度測量偏差的統計特性進行干擾參數的設計。

雷達跟蹤濾波過程中，新息V(k+1)通過增益K(·)對第k+1次的濾波輸出值產生影響(式 (5))，并進而決定了下一時刻的預測值。那么，為了使雷達能夠穩定地偏向某個方向，要求角度預測值和角度濾波值均穩定地向該方向偏離，因此，要求從統計上新息V(k+1)≥0，式 (4)中：

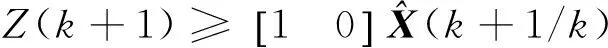
(6)

即角度測量值應大于或等于角度預測值，那么，對應于角度拖引干擾，就是勻速拖引和加速拖引兩種情況，本文討論勻速拖引和勻加速拖引兩種拖引方式。

(7)

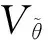
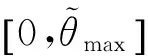
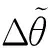
(8)

故

(9)

勻加速拖引干擾的拖引時間為

(10)

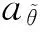
3. 實驗結果分析

3.1 角度欺騙干擾對抗仿真數學建模

本文研究針對跟蹤雷達的角度拖引干擾，為驗證其效能，首先需要對對抗雙方進行數學建模。

雷達部分的模型主要包括：天線方向圖模型(方位向兩陣元)、目標回波模型、匹配接收模型、檢測模型、距離測量模型、單脈沖測角模型(和差波束法)、角度跟蹤模型等。干擾部分的模型包括：空間幾何關系模型(如圖5所示)、干擾信號模型。圖中，L為兩干擾源之間的距離，L1為雷達天線兩陣元之間的距離，R為目標中心(兩干擾源連線中心)距雷達的距離。

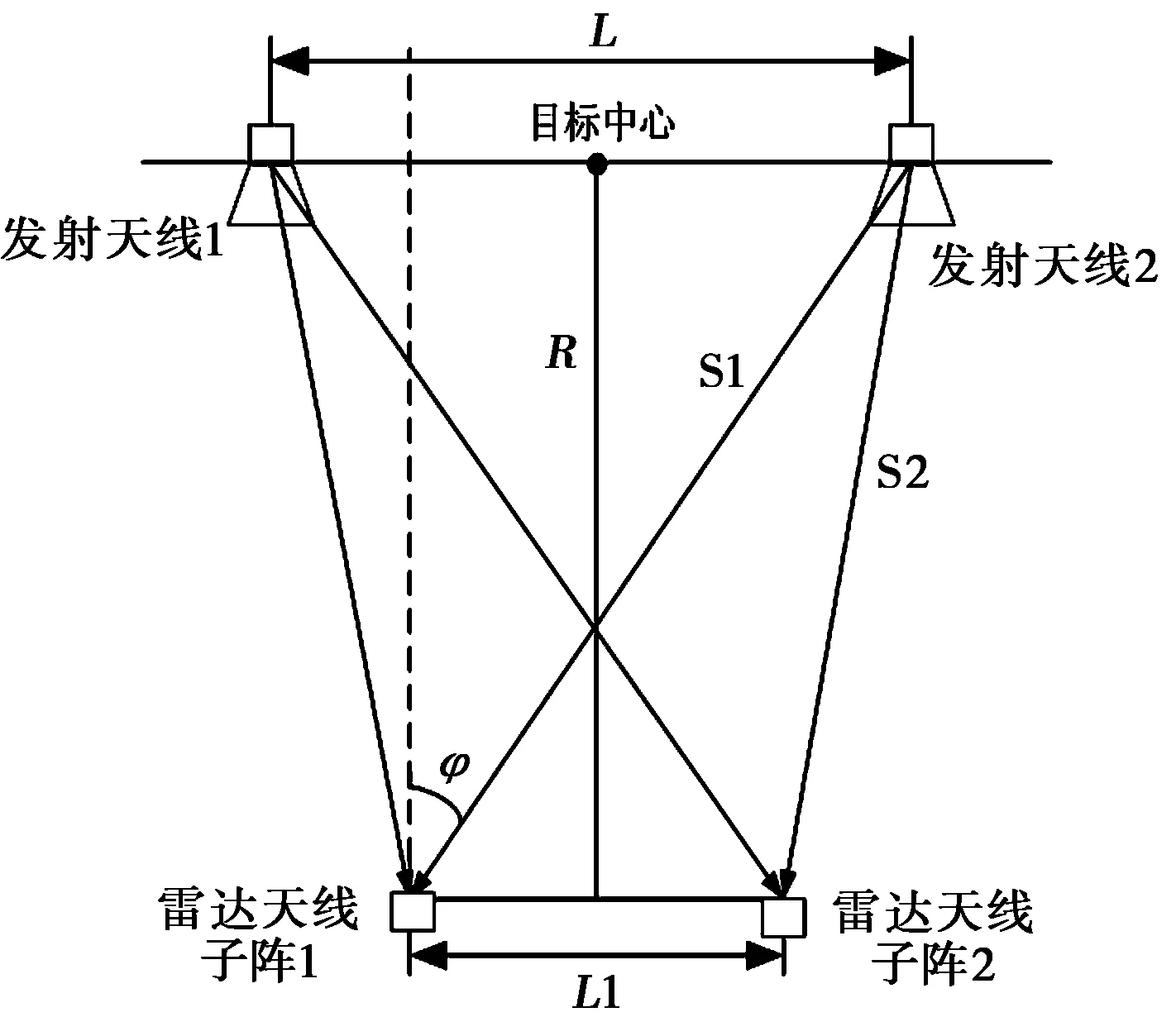
圖5 兩點源角度干擾示意圖

本文仿真中，設定目標中心以0度方位由遠及近地沿徑向飛向雷達，雷達天線初始指向為0度，采用和差波束法進行角度測量，采用α-β濾波進行角度跟蹤。角度欺騙干擾由一對轉發式假目標組成，兩假目標信號時延相同，且與真目標回波距離(時延)控制在一個距離分辨單元之內，真目標回波經匹配接收后的信噪比設為30 dB.

3.2 對常增益跟蹤濾波器的角度欺騙干擾性能

以α-β濾波器為例，分別針對常增益α-β濾波和變增益α-β濾波兩種情況檢驗勻速拖引干擾和勻加速拖引干擾的性能。

3.2.1 勻速角度拖引干擾性能仿真與分析

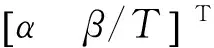
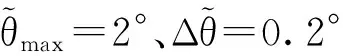
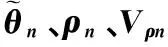
表1 勻速拖引情況下各節點的

按照上述參數進行角度拖引干擾，圖6是一次完整的角度拖引過程中的雷達角度測量/跟蹤結果。

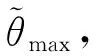
(a) 雷達角度測量值(“X”表示被剔除的野值點)

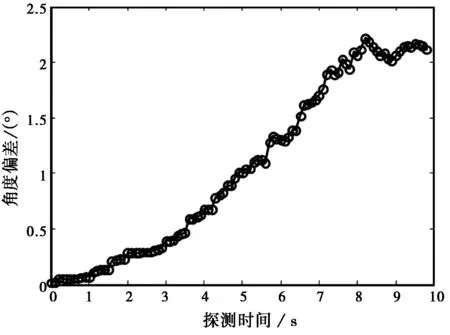
(b) 雷達角度跟蹤濾波值圖6 勻速拖引干擾下雷達角度測量/跟蹤輸出

3.2.2 勻加速角度拖引干擾性能仿真與分析

設雷達采用變增益濾波器α-β濾波器，其增益遞推衰減[6]，且

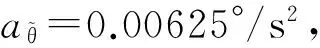
在10個節點上，對應的幅度比及其加速度速度分別如下表2所示。

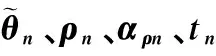
表2 勻加速拖引情況下各節點的

從表2可以看出，加速度在后期迅速增大，這是因為當超過一定范圍后其帶來的角度偏差迅速下降(如圖4示)。

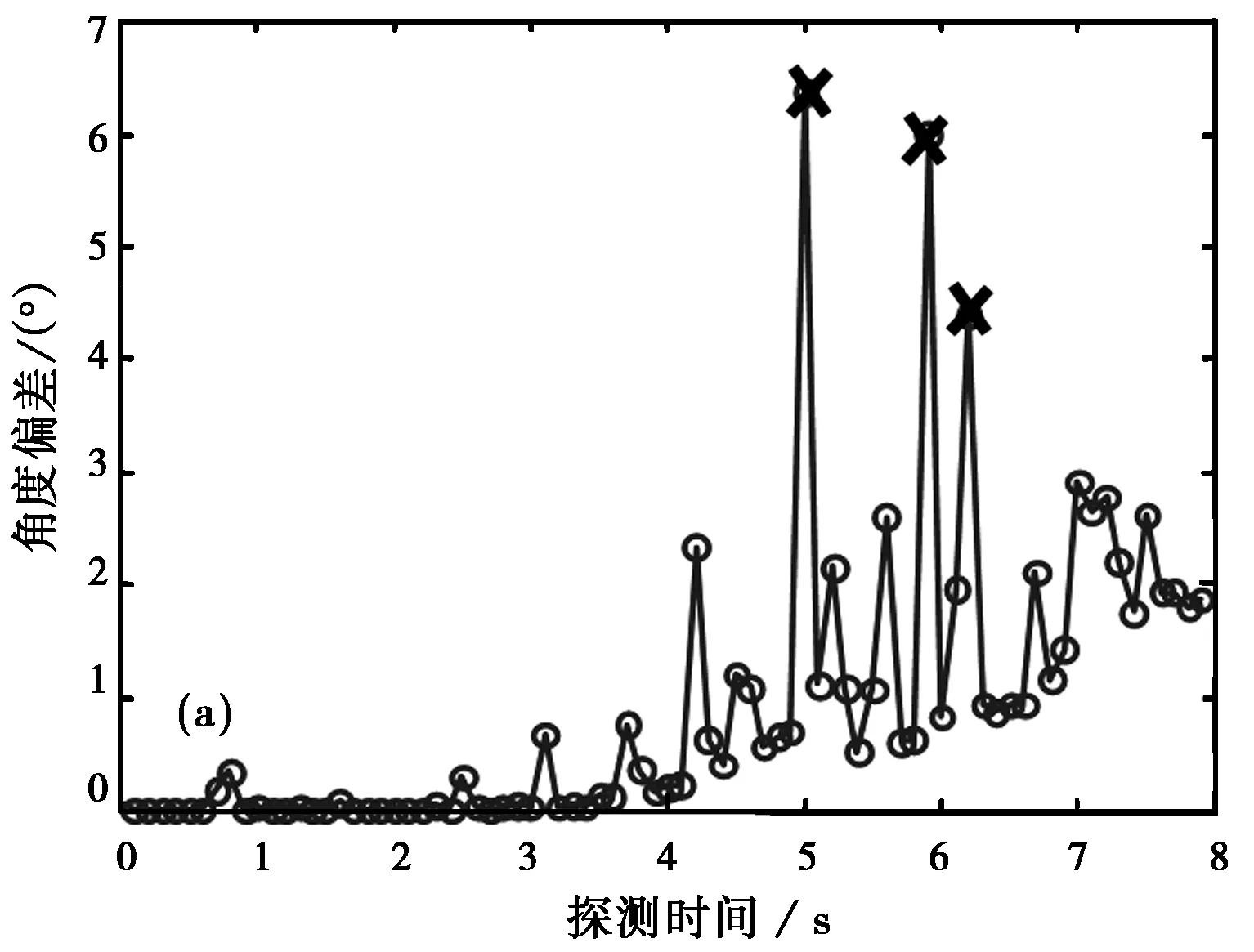
(a) 雷達角度測量值(X表示被剔除的野值點)

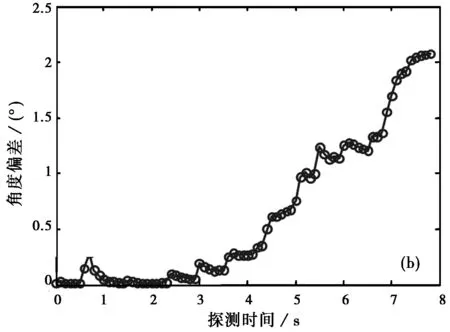
(b) 雷達角度跟蹤濾波輸出圖7 勻加速拖引干擾下雷達角度測量/跟蹤輸出

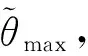
限于篇幅，本文未列出所有情況下的角度跟蹤輸出結果。實際上，在正常的雷達參數情況下，勻速拖引干擾和勻加速拖引干擾都具有與理論預期近似的拖引干擾效果。

4. 結 論

本文提出了一種新型角度欺騙干擾樣式——角度拖引干擾。該干擾立足于相位差隨機不可控情況下(如雙機編隊)的兩點源角度欺騙干擾，通過對兩點源相對幅度的設計，實現了對雷達穩定的拖引欺騙，且拖引時間較短，能夠對雷達精跟、鎖定以至于制導形成有效干擾。

文章通過對兩點源背景下雷達測角偏差統計特性的研究，并依據雷達角度跟蹤濾波器的工作機理，分別提出了勻速角度拖引和勻加速角度拖引干擾，并對其參數進行了設計。

本文給出的分析和仿真都是以雙機編隊兩點源干擾為例的，但對于相位控制精度無法達到要求的交叉眼干擾，也可以參照采用該種方法。同時，本文的研究思路和研究成果是多干擾源情況下的角度拖引干擾研究的基礎，這也是我們下一步的研究目標。

[1] SKOLNIK M I. 雷達手冊[M]. 北京: 電子工業出版社, 2003:7.5-716.

SKOLNIK M I. Radar Handbook[M]. Beijing: Publishing House of Electronics Industry, 2003: 715-716. (in Chinese)

[2] 黃培康, 殷紅成, 許小劍. 雷達目標特性[M]. 北京: 電子工業出版社, 2006: 157-165.

HUANG Peikang, YIN Hongcheng, XU Xiaojian. Radar Target Characteristcis[M]. Beijing: Publishing House of Electronics Industry, 2006: 157-165. (in Chinese)

[3] 侯民勝, 朱 瑩, 樊曉明. 單脈沖雷達的閃爍干擾技術研究[J]. 現代電子技術, 2009, 302(15): 1-3.

HOU Minsheng, ZHU Ying, FAN Xiaoming. Study on blinking jamming technique for monopulse radar[J]. Modern Electronics Technique, 2009, 302(15): 1-3. (in Chinese)

[4] 施龍飛, 王雪松, 肖順平. 低空鏡像角閃爍干擾的極化抑制[J]. 電波科學學報, 2008, 23(6): 1038-1044.

SHI Longfei, WANG Xuesong, XIAO Shunping. Depressing of angle glint of low altitude enantiomorphous target by polarization diversity[J]. Chinese Journal of Radio Science, 2008, 23(6): 1038-1044. (in Chinese)

[5] 解 凱, 陳永光, 汪連棟, 等. 距離波門拖引方案的分析建模與評估[J]. 系統工程與電子技術, 2006, 28(8): 1158-1163.

XIE Kai, CHEN Yongguang, WANG Liandong. Analysis, modeling & evaluation of range gate pull off design[J]. Systems Engineering and Electronics, 2006, 28(8): 1158-1163. (in Chinese)

[6] 王國玉, 汪連棟, 王國良, 等. 雷達電子戰系統數學仿真與評估[M]. 北京: 國防工業出版社, 2004: 141-155.

WANG Guoyu, WANG Liandong, WANG Guoliang. Simulation and Evolution of Radar and EW System[M]. Beijing: Defense Industry Press, 2004: 141-155. (in Chinese)

[7] 周宏仁, 敬忠良, 王培德. 機動目標跟蹤[M]. 北京: 國防工業出版社, 1991: 134-144.

ZHOU Hongren, JING Zhongliang, WANG Peide. Tracking of Maneuvering Targets[M]. Beijing:Defense Industry Press, 1991: 134-144. (in Chinese)