極小極大值法在賦形反射面天線設計中應用研究

張新剛 吳 剛 鐘 鷹

(中國空間技術研究院西安分院，陜西 西安 710100)

1.引 言

為提高天線的效率,減少對服務區相鄰區域的信號干擾，在衛星直播系統及宇宙通信中要求飛行器天線的輻射方向圖能與服務區形狀匹配，此即所謂的賦形。賦形反射面天線應用一個饋源照射一個表面形狀發生變化的拋物反射面天線來產生賦形波束。由于物理結構簡單、重量輕，此類天線在通訊衛星、雷達、偵察和干擾等方面具有廣泛的應用前景。

目前有很多的算法可以實現對賦形反射面天線的優化設計[1-3]，在眾多的算法中Minimax算法在實際工程應用中更加適用[4-5]，因為假如能夠實現的話，極小極大值(Minimax)算法能夠保證即使在性能最差的評估站點所得到的性能也滿足設計要求。

本文首先對計算反射面天線遠場時所用的物理光學(PO)和物理繞射(PTD)方法進行了簡單介紹，然后在用雅可比-貝塞爾(Jacobi-Bessel)函數表示反射面形狀的基礎上，以表征反射面形狀的展開系數作為變量，建立了用Minimax算法對賦形反射面天線進行優化設計的數學模型，并指出了在求解時應注意的問題，最后通過一個實際的設計例子來說明此算法在工程應用中的有效性和可行性。

2.問題的數學模型

由于反射面天線尺寸相對于工作波長(λ)屬于電大尺寸，一般采用PO法進行分析計算[6-7]，根據PO可得反射面的遠區場表達式為

(1)

Je=2(n×Hi)

(2)

式中：Hi是饋源在反射面上的入射磁場；Je是反射面表面的感生電流；n是反射面上法線的單位矢量；μ0是自由空間的磁導率；ω是角頻率；k是波數，k=2π/λ；r是觀察點所在的位置矢量；r=|r|；r0=r/r；r′是場源所在的位置矢量；S′代表反射面表面。

如果要考慮交叉極化增益或遠區旁瓣，PO法的計算精度就不能滿足要求，必須把反射面邊緣的繞射作用考慮進去。本文采用物理繞射理論[8-10]對PO方法的計算結果進行修正，以提高計算結果的精度。

(3)

式中：IT和MT分別是反射面邊緣等效電流和磁流；s是散射波單位矢量；t是反射面邊緣切向單位矢量；R=|r-r′|；Z0是自由空間特征阻抗；C是反射面邊緣的閉合曲線。

用Minimax算法對賦形反射面天線進行優化設計的一個重要前提條件就是在對反射面建模時，必須用一組完備的正交基函數來表示其形狀。應用正交基函數展開法可以保證反射面具有全局的光滑性，滿足物理光學的光滑性假設，減少優化過程中變量的數目。經常用到的有Jacobi-Bessel函數、Zernike函數、B-樣條函數等,可以根據具體需要加以選擇。

為了實現特定的設計目標而調整的變量就是設計參數，它可能包括反射面的尺寸、焦距、饋源尺寸、反射面的展開系數等。在對賦形反射面天線進行優化設計時，通常把表征反射面形狀的展開系數作為設計參數。因為展開系數是影響天線系統結構的參數，所以賦形反射面天線的優化問題是一個非線性問題。

把所有展開系數合成起來構成N維變量x=(x1,x2,…,xN)T，理論上xi可以取任何值，但是在實際應用中為了滿足特定的加工要求，對參數的取值必須加以限制。這一限制可以通過反射面的表面曲率或者反射面的形變量來加以體現。

天線的主要性能指標有增益、交叉極化隔離度、副瓣電平等。為了獲得高性能的天線，在進行優化設計時通常把指標中的一項或者幾項作為必須滿足的主要評判標準[11-12]。在服務區范圍內放置M個觀測站點來形成觀測變量y=(y1,y2,…,yM)T，然后利用反射面天線的散射場模型計算每個觀測站點的電場值，并與設計指標進行對比構成目標函數F(x,y).當以主極化增益和交叉極化隔離度作為主要評判標準時，具體形式如下式所示

F(x,y)= (F1(x,y1),…F1(x,yM),

F2(x,y1),…F2(x,yM))T

(4)

F1(x,yi)=wi[D1(yi)-fco(x,yi)]

1≤i≤M

(5)

式中：wi是第i個觀測站點的權重系數；D1(yi)、D2(yi)分別是第i個觀測站點設計要求的主極化電場值和交叉極化隔離度值,fco(x,yi)、fcross(x,yi)分別是設計參量為x的情況下第i個觀測站點的主極化和交叉極化電場的計算結果。

Minimax方法就是通過優化變量x來使得目標函數F(x，y)的最大值最小化，可以寫成如下的形式

(6)

(7)

即在x的某個限定范圍內，尋找能夠使函數ψ(x)取值最小的點x*.基于一種限步長的梯度迭代算法[13]，以Matlab作為編程工具，自編了一個求解Minimax問題的優化程序來進行仿真計算，得到了比較理想的結果。

另外一個值得注意的問題是由于賦形反射面天線的設計問題是凹的最優化問題，梯度算法并不能保證所得到的結果是全局最優解。在實際設計過程中，為了使設計結果盡可能接近全局最優解，必須選擇合適的初始狀態，防止觀測站點正好位于副瓣上。

3.設計實例

通過一個設計實例來說明Minimax算法在賦形反射面天線設計問題中的有效性。

此設計的目標是設計一個波束覆蓋巴西全部領土的單偏置拋物反射面天線，衛星位于地球靜止軌道，定點西經55°上空。在此設計中，把主極化增益和交叉極化隔離度作為主要的評判指標，要求在服務區范圍內，主極化增益至少要達到28 dBi，交叉極化隔離度要在21 dB以上，服務區形狀及其觀測站點如同圖1所示。

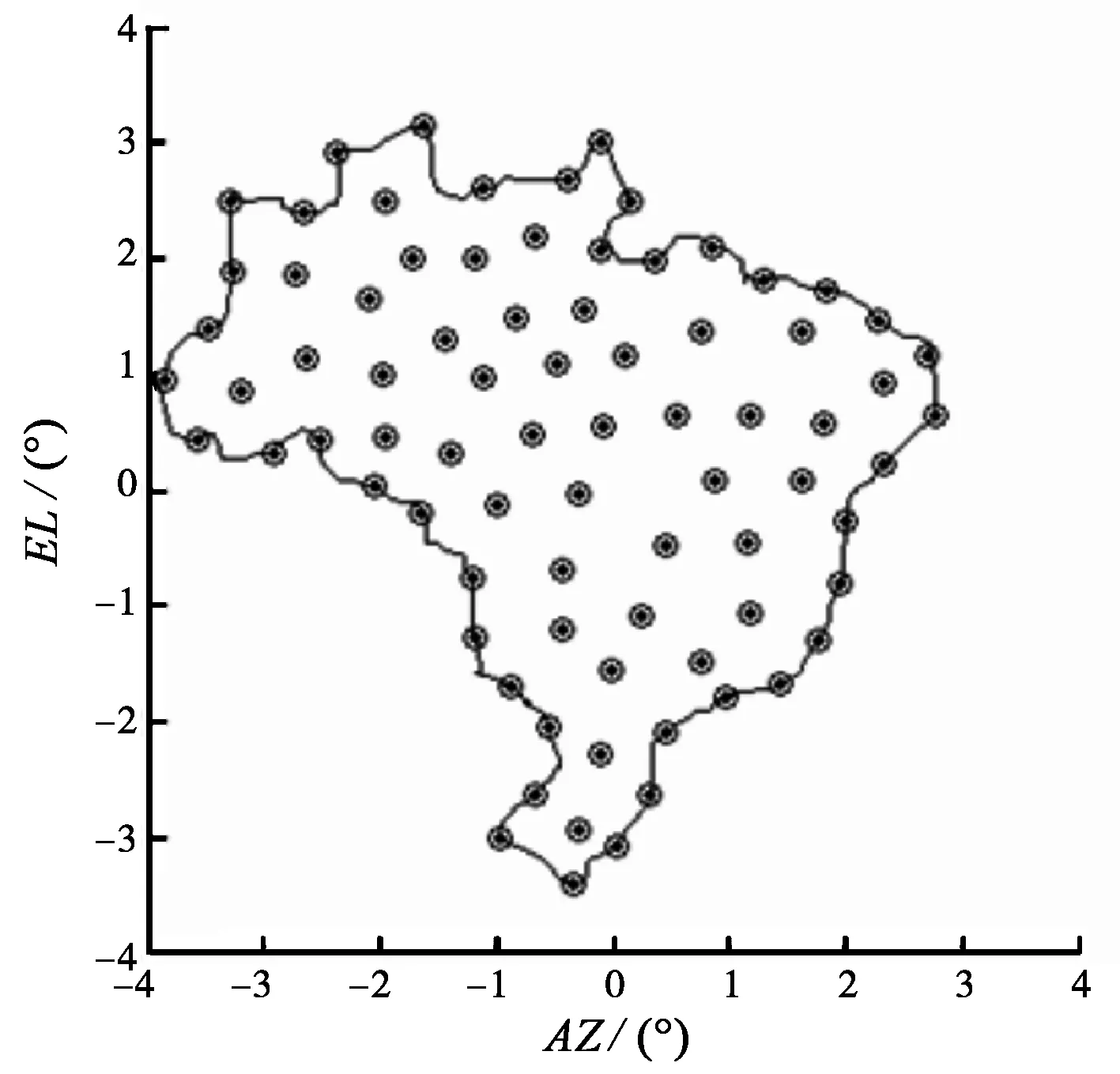
圖1 服務區形狀及其站點位置示意圖

單偏置拋物反射面天線結構示意圖如圖2所示，在本次設計過程中，所采用的具體設計參數如下：單偏置拋物反射面口徑投影的直徑D=2a=1.524 m，焦距f=1.506 m，H=1.245 m，θ=42.77° ，饋源采用x極化的 (cosθ)q式饋源，在反射面邊緣有-12 dB(q=14.28)的凋落，設計的工作頻率為11.95 GHz.

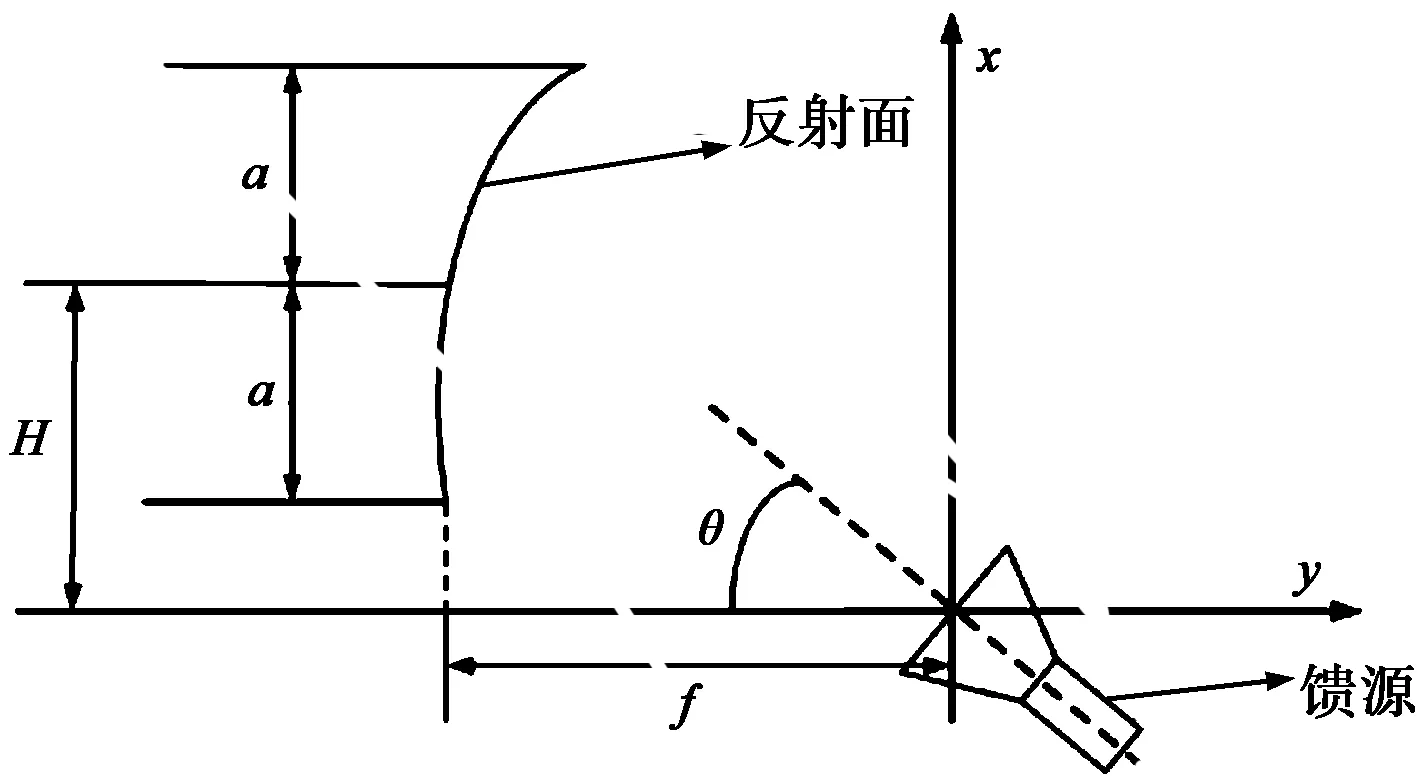
圖2 單偏置拋物反射面天線結構示意圖

反射面表面用Jacobi-Bessel函數來對反射面表面進行展開，具體形式如下

(8)

標準的單偏置拋物反射面天線在遠區場等值線圖如圖3所示。從圖中可以看出：在服務區域內，其輻射能量分布是十分不均勻的，在中心區域高達44 dBi，而在邊緣區域則低于10 dBi.天線的輻射方向圖與服務區形狀不匹配，因此，在實際衛星通信系統中不能直接采用此類天線，必須對其進行優化設計。

采用Minimax算法對反射面天線進行優化時，標準的單偏置拋物面不能選為初始狀態。從圖3中可以看到：此時天線的副瓣位于要求的服務區內。假如某個采樣站點正好位于副瓣上，用Minimax算法進行優化時，無論如何調節都會造成此站點增益的降低，優化就有可能困于這個錯誤結果而無法進行下去。因此，必須在標準單偏置拋物面的基礎上疊加一個形變來防止上面情況的出現，所疊加型變量的具體計算公式如下式所示[14]

(9)

x1=(x-x0)cos(α)+(y-y0)sin(α)

y1=-(x-x0)sin(α)+(y-y0)cos(α)

(10)

式中：μ0、ν0是在(μ,ν)坐標系下環繞覆蓋區域橢圓的中心坐標，ω1、ω2是橢圓的半軸長度；α是橢圓的旋轉角度。x0、y0是天線口徑的中心坐標，D、f分別是天線的口徑和焦距。

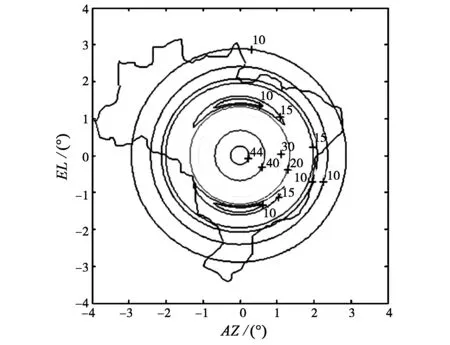
圖3 標準偏置拋物反射面遠區場等值線圖(單位:dBi)

仿真中參數μ0、ν0、ω1、ω2、α的取值分別為-0.00349、-0.00175、0.0995、0.0436、54.46°，在標準單偏置拋物反射面的基礎上疊加此形變量后，得到天線的遠區場等值線圖如圖4所示。由圖可見：在服務區內不存在副瓣，可以避免采樣站點正好位于副瓣上的情況出現，保證優化程序順利進行。

圖4 標準偏置拋物反射面疊加形變量后遠區場等值線圖 (單位:dBi)

在天線的基本參數和初始狀態確定以后，用Minimax算法對反射面表面展開系數Cnm和Dnm進行優化，經過150次迭代后，得到如圖5所示的主極化增益等值線圖。如果所疊加的形變量不合適，優化開始時服務區內存在副瓣，即使經過更多次的迭代，也無法收斂到較好的結果。相反，只要保證服務區內沒有旁瓣，疊加不同的形變量對算法收斂性無明顯影響。因此，在對參數μ0、ν0、ω1、ω2、α進行取值時，只要使所確定的橢圓基本上能把服務區包含在內，保證服務區沒有旁瓣即可，對橢圓的具體大小和位置不必過分關注。

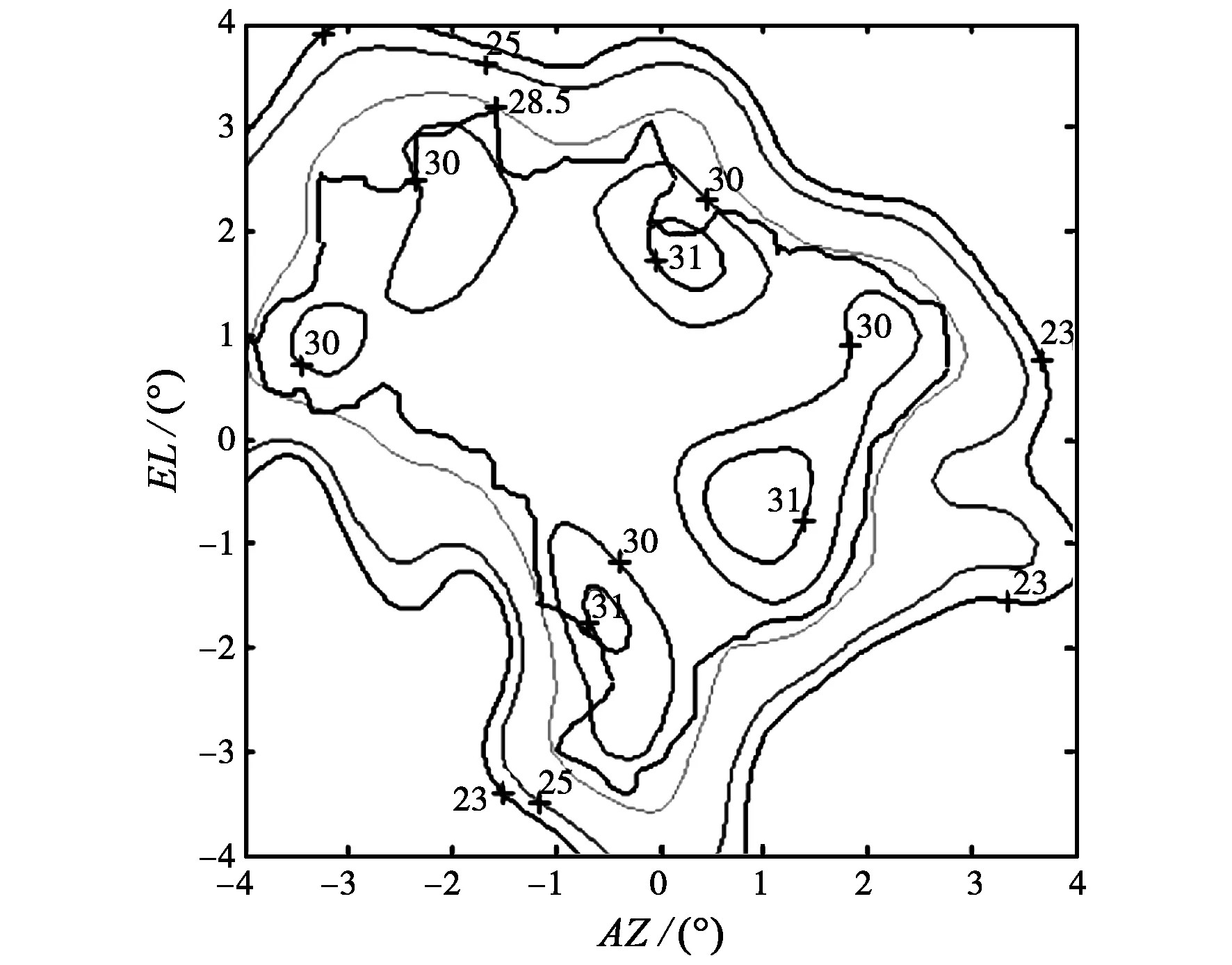
圖5 優化后主極化增益等值線圖 (單位:dBi)

從圖5中可以看到：在巴西所有的領土范圍內，主極化增益都在28.5 dBi以上,并且在約30%的區域內高于30 dBi，比設計要求的28 dBi至少高出0.5 dB.能量在整個服務區內分布比較均勻，與服務區形狀匹配。應用于衛星通信系統中作為發射天線時，只需要生產一種型號的地面接收設備(能接收到增益為28.5 dBi的信號)，就可以在整個巴西領土范圍內任意一點接收到衛星信號。圖6給出了優化后服務區的交叉極化隔離度等值線圖，由圖可見：在服務區內任何一點交叉極化隔離度都在21 dB以上，并且在60%以上的區域，交叉極化隔離度在25 dB以上。

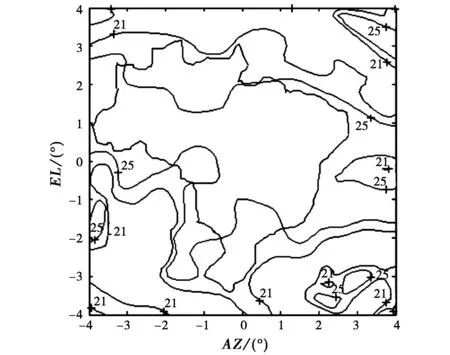
圖6 優化后交叉極化隔離度等值線圖(單位:dB)

優化后反射面相對于標準單偏置拋物面形變量的等值線圖如圖7所示。可見優化后反射面形變量在(-0.8λ，0.4λ)范圍內，而且沒有發生突變的區域，整個表面比較光滑，滿足實際加工要求。

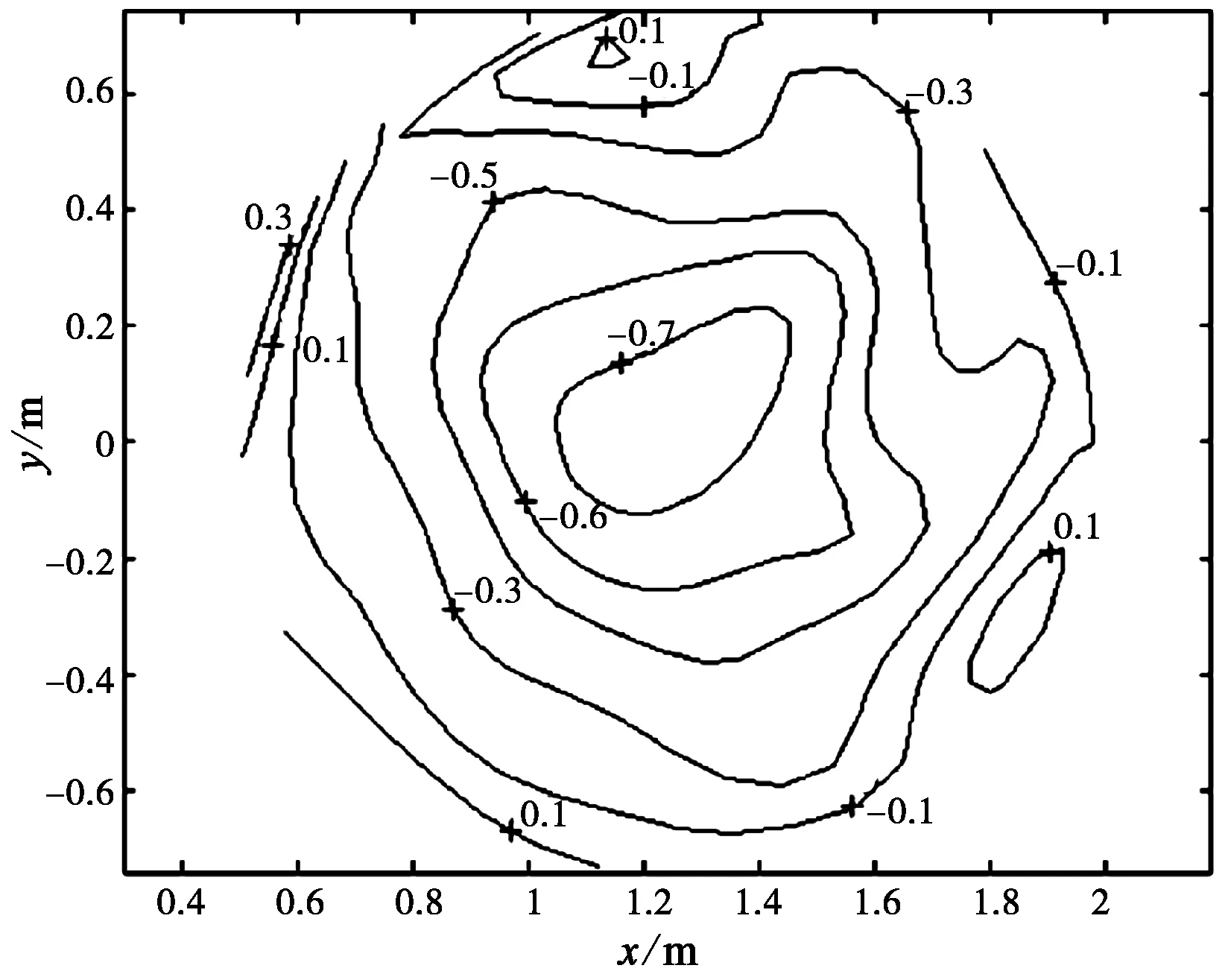
圖7 優化后反射面形變量等值線圖 (單位:λ)

4.結 論

為得到覆蓋整個巴西領土的對主極化增益和交叉極化隔離度都有嚴格要求的賦形波束，本文建立了用Minimax算法對單偏置拋物反射面天線進行優化設計的數學模型并進行了仿真計算。從數值模擬結果可以看出，在服務區內主極化增益都在28.5 dBi以上,交叉極化隔離度都在21 dB以上，完全滿足設計指標要求。優化得到的反射面表面比較光滑，滿足實際加工要求。優化結果對工程應用具有重要的參考價值，此優化方法還可以用于星載多波束賦形和在軌重構方面。

[1] CHOU H, CHOU H T. Fast SDM for shaped reflector antenna synthesis via patch decompositions in PO integrals[J]. Progress In Electromagnetic Research, PIER, 2009, 92:135-151.

[2] DUAN D W, RAHMAT-SAMII Y. A generalized diffraction synthesis technique for high performance reflector antenna[J]. IEEE Transactions on Antennas and Propagation,1995, 43( 1):27-39.

[3] AVILA S L, CARPES W P, VASCONCELOS J A. Optimization of an offset Reflector Antenna Using Genetic Algorithms[J]. IEEE Transactions on Magnetics, 2004, 40(2): 1256-1259.

[4] JACOBSEN H S, MADSEN K. Synthesis of nonuniformly spaced arrays using general nonlinear minimax optimization method[J]. IEEE Trans, 1976,24:501-506.

[5] KLEIN C A. Design of shaped-beam antennas through minimax gain optimization[J]. IEEE Trans, 1984, 32: 963-968.

[6] 李 鵬，張志華，王 為，等. 基于不同網格形式的反射面天線方向圖分析[J]. 系統工程與電子技術,2009,31(2):347-351.

LI Peng, ZHANG Zhihua, WANG Wei, et al. Far field pattern numerical analysis of reflector antenna based on different grid forms[J]. Systems Engineering and Electronics, 2009, 31(2):347-351.(in Chinese)

[7] 王 偉，段寶巖，馬伯淵. 重力作用下天線反射面形變及其調整角度的確定[J]. 電波科學學報，2008，23(4):645-650.

WANG Wei, DUAN Baoyan, MA Boyuan. Gravity deformation and best rigging angle for surface adjustment of large reflector antennas[J]. Chinese Journal of Radio Science,2008,23(4):645-650.(in Chinese)

[8] JOHANSEN P M. Uniform physical theory of diffraction equivalent edge currents for truncated wedge strips[J]. IEEE Trans, 1996, 44:989-995.

[9] 馮 林，鄧書輝，阮穎錚. 反射面天線帶內雷達散射截面[J]. 電波科學學報，1996，11(2):18-21.

FENG Lin, DENG Shuhui, RUAN Yingzheng. Reflector antenna's RCS in operating band[J]. Chinese Journal of Radio Science, 1996, 11(2):18-21.(in Chinese)

[10] 肖 疆，徐曉文，董 濤. 多孔毀傷時賦形反射面天線輻射特性的研究[J]. 電波科學學報，2003，18(6):648-651.

XIAO Jiang, XU Xiaowen, DONG Tao. Study on the radiation characteristics of a shaped beam reflector antenna under the multi-hole damnification[J]. Chinese Journal of Radio Science, 2003, 18(6):648-651. (in Chinese)

[11] BENDIMERAD M F, MERIAH S. Design of linear antenna arrays for side lobe reduction using the tabu search method[J]. The International Arab Journal of Information Technology, 2008, 5(3): 219-222.

[12] PUJARA D A. Improving the beam efficiency of an offset parabolic reflector antenna for space-borne radiometric application[J]. Progress In Electromagnetic Research C, 2009, 10:143-150.

[13] MADSEN K. An algorithm for minmax solution of over determined systems of non-linear equations[J]. J. Inst. Math Applics,1975,16: 321-328.

[14] HAYES S G. Shapes for Reflector Antennas[D]. Brisbane Australia: University of Queensland, 1993.