平面波在時域有限差分法中的引入方法研究

柴焱杰 孫繼銀 孫東陽 胡 寅

(1.第二炮兵工程學院，陜西 西安 710025； 2.西北核技術研究所，陜西 西安 710024； 3.第二炮兵指揮學院，湖北 武漢 430012)

1.引 言

時域有限差分法(FDTD，The finite difference time domain method)是研究電磁問題的一種迅速發展的仿真計算方法，能夠在時域直接計算得到寬帶結果，適合于分析復雜電磁系統。引入平面波激勵源是各類電磁仿真研究的重要內容，是進行場效應計算的基礎前提[1-5]。FDTD中，仿真平面波激勵源時使用總場-散射場(TF-SF)連接邊界條件[6]，如圖1所示。

圖1 FDTD總場-散射場計算模型

根據等效原理，在連接邊界上設置平面波的等效面電磁流，并設平面外的場為零，就可將入射波只引入到總場區。連接邊界上的等效電磁流為

(1)

式中：en為面的外法向；Ei、Hi分別為入射電場(V/m)和入射磁場(A/m)。通常使用球坐標系描述平面波激勵源的傳播方向和極化狀態，使用三維直角坐標系進行FDTD迭代運算，因此，需要解決平面波激勵源的投影問題，如圖2所示[7]。

圖2 HEMP平面波使用的球坐標系

圖2中α是極化角，坐標系中的原點O位于連接邊界貼近三維直角坐標系中FDTD計算空間原點的那個角點。由于平面波傳播方向k由角度(θ，φ)標定，而一般情況下FDTD仿真計算模型位于第一卦限中，因此，當入射角超越這個范圍，將會引起平面波不能“照射”(引入)到計算區域內的情況。為方便研究，使計算模型更為靈活、符合實際情況，研究兩種任意角度引入平面波激勵源的方法， 并對其仿真效果進行評價。

2.理論分析

2.1 基于角點延遲引入任意角度平面波[6-9]

為使任意角度平面波能夠入射到仿真空間，將三維FDTD連接邊界上的八個角點編號O1～O8，如圖3所示。角點延遲的思想是，當平面波以任意角度(θ，φ)入射該區域時，無論該角度是多少，總可以認為該平面波是以其中某一角點出發引入進來的。

圖3 連接邊界上的角點編號

由于平面波傳播方向k在直角坐標系統中的投影為

er=(kx,ky,kz)

=(sinθcosφ,sinθsinφ,cosθ)

(2)

因此，三個分量kx、ky、kz反映了從原點O出發的k在哪個卦限的信息，從而可選擇某一角點作為基準點Os，用以計算一維平面波相對一維源點的延遲距離。設點變量Os(INCX,INCY,INCZ)是平面波的出發點，依據kx、ky、kz的符號可按表1的選擇條件確定基準點Os.

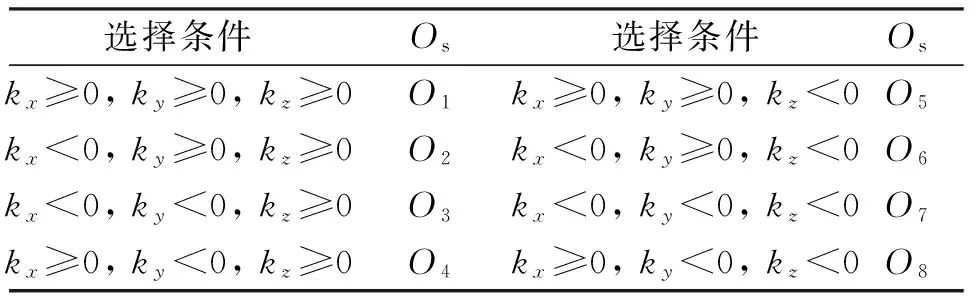
表1 基準點Os的確定

圖3中同時示出了以O2點作為基準點Os的情況。當入射平面波的方向矢量er滿足條件：kx<0,ky≥0,kz≥0，此時平面波將入射到第二卦限。選擇O2點作為基準點Os，即平移原入射方向，就能夠保證平面波進入到FDTD總場空間中。

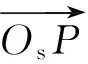
(3)

根據延遲距離r′計算出某點的場量后，即可轉換為連接邊界上該點的切向場分量：

(4)

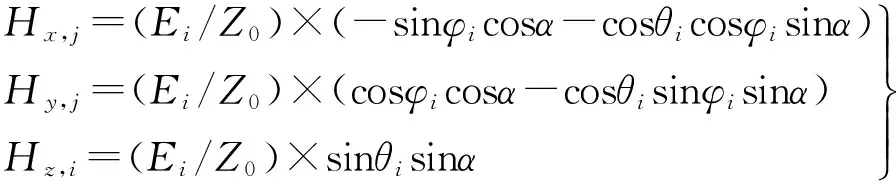
(5)

由式(4)、(5)計算出的電、磁切向場分量可實現任意角度平面波在三維FDTD中的傳播。根據延遲距離r′計算場量的方法主要有兩種——一維平面波推進法和解析法。需要注意的是，無論是一維平面波推進法還是解析法，由于電場E和磁場H在空間上相隔半個空間步，而在八個基準點Os上均沒有場量，因此需要仔細推算連接邊界上的場點與基準點之間的實際距離r′，這是實現正確投影和坐標系統轉換的前提。

2.2 一維平面波推進法

一維平面波推進法將入射平面波用一維FDTD隨時間逐步推進的方式提供連接邊界上的切向場分量。一維FDTD平面波由式(6)表述。

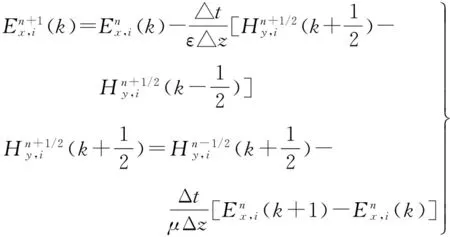
(6)

一維FDTD場點的網格其時間步長、空間步長與三維FDTD計算空間相同。一維FDTD區域的邊界應留有若干網格以便加入吸收邊界條件。一維FDTD總長度與總場空間(連接邊界內的區域)有關，應滿足條件

(7)

式中：ZNX、ZNY、ZNZ是三維FDTD中總場空間三個方向上的長度(網格數)；UNZ是一維FDTD吸收邊界的厚度(網格數)。

r′標明了一維FDTD平面波上與三維FDTD連接邊界中的P點所對應的坐標位置。r′有時可能不是整數，設r′=(p+w)△x，0

(8)

2.3 解析法

(9)

3.實驗結果與分析

為驗證算法的正確性，選擇高空核爆電磁脈沖(HEMP，High-altitude electromagnetic pulse)作為研究對象。HEMP是指發生在30 km以上的高空核爆炸產生的電磁脈沖，是電磁兼容等領域研究的重要內容。當前應用比較廣泛的描述HEMP波形的標準有1976年出版物標準、Bell實驗室標準和國際電工委員會(IEC)制定的HEMP標準等[10]。這些對HEMP的描述中，將HEMP輻射波形擬合為雙指數函數表達式，其中IEC制定的HEMP標準波形為

E(t)=1.3×5×104×(e-4×107×t-e-6×108×t)

(10)

IEC定義的HEMP時域波形和歸一化頻譜如圖4所示。從圖4可見，HEMP峰值達到50,000 V/m；上升時間和衰落時間分別是2.5 ns和55 ns；波形能流分布的主要頻段范圍(能流比例在98%)是100 kHz～100 MHz[11]。因此，HEMP具有高峰值場強、快上升沿、寬頻帶等特點，會對電子設備構成嚴重威脅。

圖4 IEC標準定義的HEMP波形及其歸一化頻譜

當使用一維平面波推進法引入HEMP平面波時，一維FDTD源點的HEMP脈沖波形離散化為

e-6×108×(n+1)×Δt)

(11)

式中，k0是源點的位置，某位置的一維平面波場量由式(6)遞推得出。為使用解析法引入HEMP平面波，延遲距離為r′的某點其HEMP的電場值離散化為

(12)

3.1 計算實例

為滿足Courant穩定性條件以及控制數值色散，可設置網格大小Δs=c/(20fm)=0.15 m，時間步長Δt=Δs/(2c)=0.25 ns.為便于觀察，將總網格數目設置為90×90×90，其中總場區的網格數目為60×60×60。圖5(見413頁)是θ=90°，α=180°，φ=0°時使用一維平面波推進法計算場值Ez隨時間步推進的兩個網格圖片段。

為比較兩種引入HEMP平面波方法的效果，設置θ=90°，α=180°，φ=0°、135°，此時電場E只有z分量。取z=NZ/2(位于計算空間一半高度的平面)為觀察面。兩種方法計算HEMP平面波傳播的等高線圖如圖6(見413頁)所示。最后，設置幾種網格尺寸，對幾種情況下入射電場在散射場區泄露的最大值進行統計和比較，結果如表2、表3所示。

表3 φ=135°時，入射電場在散射場區泄露的最大值 /(V/m)

3.2 仿真結果分析

由圖5～6，表2～3可以看出：

1)φ=0°時，基準點為O1，HEMP平面波的k應沿x軸方向；φ=135°時，基準點為O2，HEMP平面波的k應沿-x軸與y軸中間45°方向。從仿真結果可以看出，基于兩種方法的場波形均沿正確的方向傳播。

2) 一維平面波推進法中，由于一維FDTD存在的數值色散能夠很大程度上抵消三維FDTD存在的固有數值色散，因而總場區域內的結果比較準確，總場區域外則較為純凈。解析法雖然計算出了連接邊界上各點的準確值，卻因不能抵消這種數值色散，而在波前附近出現了幅值較大的電場泄露；總場區域內也出現了不均勻的現象：等高線圖中出現了較多的噪點，總場區中亦出現較多的曲線，這有悖于平面波的均勻特性。

3) 在一維平面波推進法的計算結果中可以發現，當φ=0°時，一維FDTD平面波與三維FDTD空間的網格大小吻合，沒有實際的插值現象，入射電場在散射場區的泄露非常小，接近于計算機的基本計算誤差，結果很理想；當φ=135°時，由于在r′為非整數的位置使用了插值的方法(如式(8))，此時亦出現了少許波的溢出現象，然而，入射電場在散射場區的泄露會隨著網格尺寸的減小而減小，即減小網格尺寸能夠明顯降低HEMP的泄露。從泄露的最大值上看，一維平面波推進法要明顯優于解析法。

4.結 論

在論述基于角點延遲思想的基礎上，從原理上推導了將HEMP平面波引入到三維FDTD中的兩種方法——一維平面波推進法和解析法，解決了任意入射角度HEMP平面波引入三維FDTD計算空間的問題。對HEMP平面波在自由空間的傳播過程進行了仿真驗證和比較。結果表明:兩種方法都能以任意角度將平面波引入到總場區域，計算代價小；一維平面波推進法很大程度上抵消了FDTD法的數值色散誤差，溢出波較少，而解析法出現了較多的溢出波。工程應用中如果使用一維平面波推進法，可通過適當減小網格尺寸進一步改善平面波的仿真效果。

[1] 劉順坤, 聶 鑫, 陳向躍. 電磁脈沖對電纜耦合問題的理論研究[J]. 電波科學學報, 2010, 25(2): 348-352.

LIU Shunkun, NIE Xin, CHEN Xiangyue. Numerical study on cable coupling effects excited by electromagnetic pulse [J]. Chinese Journal of Radio Science, 2010, 25(2): 348-352. (in Chinese)

[2] TESCHE F M, IANOZ M V, KARLSSON T. EMC Analysis Methods and Computational Models[M]. New York: John Wiley & Sons, Inc., 1997.

[3] SULLIVAN D M. Electromagnetic Simulation Using the FDTD Method[M]. Idaho: IEEE Press, 2000.

[4] 高本慶, 薛正輝, 任 武. FDTD計算中關于低頻激勵源問題的研討[J]. 電波科學學報, 2009, 24(2): 213-217.

GAO Benqing, XUE Zhenghui, REN Wu. Study on low frequency exciting source in FDTD simulation [J]. Chinese Journal of Radio Science, 2009, 24(2): 213-217. (in Chinese)

[5] 董 慧, 李清亮, 閆玉波, 等. 三維大尺寸介質目標散射問題的總場邊界PSTD技術[J]. 電波科學學報, 2005, 20(4): 434-439.

DONG Hui, LI Qingliang, YAN Yubo, et al. Application of TB-PSTD algorithm to the scattering of 3-D large dielectric objects[J]. Chinese Journal of Radio Science, 2005, 20(4): 434-439. (in Chinese)

[6] TAFLOVE A, HAGNESS S C. Computational Electrodynamics:The Finite-Difference Time-Domain Method[M]. 2nd ed. Boston: Artech House, 2000.

[7] 葛德彪, 閆玉波. 電磁波時域有限差分方法[M]. 2版. 西安電子科技大學出版社, 2006.

GE Debiao, YAN Yubo. The finite differrence time domain method of electromagnetic[M]. 2nd ed. Xi’an Electronic Science and Technology University Press, 2006. (in Chinese)

[8] 王長清. 現代計算電磁學基礎[M].北京： 北京大學出版社, 2005.

WANG Changqing. Foudation of Computational Electromagnetism[M].Beijing: Beijing University Press, 2005. (in Chinese)

[9] 莊釗文, 袁乃昌, 莫錦軍, 等. 軍用目標雷達散射截面預估與測量[M]. 北京: 科學出版社, 2007: 163-164.

ZHUANG Zhaowen, YUAN Naichang, MO Jinjun, et al. Estimate and measurement of martial object’s RCS[M]. Beijing: Science Press, 2007: 163-164. (in Chinese)

[10] 謝彥召, 孫培云, 周 輝, 等. 地面附近高空核爆電磁脈沖環境[J]. 強激光與粒子束, 2003, 15(7): 680-684.

XIE Yanzhao, SUN Beiyun, ZHOU Hui, et al. High-altitude electromagnetic pulse environment over the lossy ground[J]. High Power Laser and Particle Beams, 2003, 15(7): 680-684. (in Chinese)

[11] 謝彥召, 王贊基, 王群書, 等. 高空核爆電磁脈沖波形標準及特征分析[J]. 強激光與粒子束, 2003, 15(8): 781-787 .

XIE Yanzhao, WANG Zanji, WANG Qunshu, et al. High altitude nuclear electromagnetic pulse waveform standards: a review [J]. High Power Laser and Particle Beams, 2003, 15(8): 781-787. (in Chinese)