基于盲源分離的自適應抗干擾算法研究
柯熙政 劉 娜
(西安理工大學自動化與信息工程學院,陜西 西安 710048)
1.引 言
衛星導航系統中的自適應抗干擾問題一直是近些年來研究的熱點,多數算法討論的是基于均勻線陣(ULA),但ULA僅可估計信號的一維到達角,并只能提供180°的方位信息[1]。而均勻圓陣可提供360°的方位角信息,同時也可提供俯仰角信息,并且具有圓對稱特性,其方向特性在方位角方向上近似各向同性。所以研究圓陣的自適應抗干擾算法有著其理論意義和實際價值。自適應算法處理能自動將主瓣對準期望信號,將零陷對準干擾[2]。經典的波達方向(DOA)估計算法如多重信號分類(MUSIC)、旋轉不變子空間(ESPRIT)算法[3-4],可以很準確地測得信號的波達方向,因為期望信號很小,所以測得的角度直接就是功率大的干擾信號。在得到干擾信號的DOA后,采用基于DOA估計的最小方差響應無畸變(MVDR)的波束形成算法在干擾處形成零陷,這種MUSIC與MVDR相結合的自適應算法適應于強干擾威脅的環境。
當干擾信號與期望信號相當時,采用上述MU-SIC結合MVDR算法則不能在干擾處形成合適零陷,原因是MUSIC所測得DOA信息中,不僅僅是
干擾的DOA,同時也有期望信號的DOA信息,如果直接采用MVDR算法在所測得DOA角處進行抑制,則抑制干擾的同時期望信號也被抑制掉了,從而導致算法失效。鑒于這個原因,文章基于圓陣首先采用高分辨二維方向估計的MUSIC算法估計出所有信號的DOA信息,然后利用快速獨立分量分析(FastICA)算法估計出各個源信號,將分離出的源信號與DOA對應,采用相關方法例如特征提取、信號調制方式、信號出現位置等方法區別有用信號與干擾信號,最后利用MVDR算法在干擾處形成零陷,方案框圖如圖1所示。這個方案利用了高分辨方向估計和數字波束形成的有關成果,一定程度上可以在期望信號與干擾信號相當的情況下抑制干擾,仿真證明了該方法的可行性。

圖1 方案框圖
2.信號模型
假設有P個信源分別從不同的方向到達均勻圓陣,λ為工作波長,由于中心有陣元的均勻圓陣在同樣的陣元數時,可以使得主瓣更窄,副瓣更低,從而有效地抑制主瓣以外的干擾[5],所以在這選取中心有陣元的均勻圓陣,如圖2所示為一個七元均勻圓陣示意圖。

圖2 均勻圓陣實體圖
圓陣半徑R如式(1)所示,M為陣元個數。
(1)
圓周上的各陣元分布角度分別為
(2)
假設有P個信號源到達天線陣列,則陣列結構可以表示為
A=[a(θ1,φ1),a(θ2,φ2),…,a(θp,φp)]
(3)
式中,(θi,φi)為第i個信源到達陣列的俯仰角和方位角。
(4)
所以,陣列天線的接收信號可以表示為
X(t)=AS(t)+n(t)
(5)
式中:S(t)=[s1(t),s2(t),…,sp(t)]T為入射信號;n(t)=[n1(t),n2(t),…,nM(t)]為加性白噪聲。
3.干擾信號與有用信號相比擬時的抗干擾算法
當干擾信號與有用信號功率相比擬時,MUSIC算法測得所有信號的DOA信息,采用盲源分離的方法分離出各個源信號,再將分離出的源信號與所測得DOA進行對應,利用相關方法區分出干擾與有用信號的方向,利用MVDR算法在干擾處進行抑制。
3.1 MUSIC算法[6-7]
該算法的基本思想是將陣列輸出數據的協方差矩陣進行特征分解,從而得到與信號分量相對應的信號子空間和與信號分量相正交的噪聲子空間,然后利用這兩個子空間的正交性來估計信號的DOA。
MUSIC譜峰值由下式給出[8],即
(6)
式中:a(θ,φ)為信號分量的導向矢量;V為噪聲特征向量構成的矩陣。
3.2 FastICA算法
FastICA算法是一種盲源分離[9]算法,是指僅利用源信號的觀測信號恢復源信號的各個獨立成分。本文在研究FastICA[10]的基礎上,將之應用于陣列信號的提取中。算法模型如圖3所示。

圖3 算法模型
FastICA算法的過程如下:
接收矩陣如公式(5)所示,對公式(5)進行系列處理:
1) 去均值和白化
Q=vg-1/2vT
(7)
式中:v是由協方差矩陣的特征向量組成的正交矩陣;g是由與特征向量對應的特征值組成的對角陣。則白化信號

(8)
2) 迭代過程
盲源分離的權向量的計算公式[11]為
w(n+1)=E{Z(w(n)TZ)3}-3w(n)
(9)

(10)
3) 收斂條件
w(n),w(n-1)的內積絕對值處于1+u與1-u之間,即足夠接近1,這樣一直循環,直至滿足收斂條件。(u為步長因子,一般取很小的值)
3.3 MVDR算法
該算法是一種自適應波束形成[14]技術,通過對各陣元的加權進行空域濾波,來達到增強期望信號、抑制干擾的目的,利用MUSIC算法得到信號的DOA后,為了使干擾最大程度抑制,就必須在干擾信號的DOA處進行抑制,實現手段就是調節陣列的權矢量。
所以在采用MVDR算法前,必須在MUSIC所測得的所有DOA信息中,找到干擾信號的DOA,這里采用最小均方差準則,即用所測的DOA角組成的不同陣列結構分別與盲源分離結果作積,然后將所得積與接收信號作差求平方,最小值對應的陣列結構則對應分離出的源信號。找到各信號對應的DOA后,再通過特征提取、信號調制方式、信號出現位置等方法區分出有用與干擾信號,最后使用該算法在干擾處形成零陷。
陣列的輸出是陣列接收信號在各陣元上的加權和,設波束(零陷)形成的權向量為
w=[w1,w2,…,wM]T
(11)
陣列輸出為
y(n)=wHX(n)
(12)
假設陣列輸出的功率為p,則
(13)
為了在期望方向上增益為1,假設θ為入射方向,則[15]
(14)
構造拉格朗日算子[16],令目標函數
L(w)=wHRXXw+λ[wHa(θ)-1]
(15)
解方程得最佳權向量
wopt=μRXX-1a(θ)
(16)
將約束條件代入,可得
(17)
將式(16)和(17)綜合,得
(18)
以上情況是針對期望信號是一個,若同時有幾個期望信號,可以將最終權值形成稍作變化,即
(19)
式中e根據具體情況而定,例如假設有四路信號,其中第二路和第三路為干擾,其余為期望,則e=[1,0,0,1]T.
4. 計算機仿真與分析


s1=rvar1*rand(1,N)
s2=rvar2*cos(2*π*(50*0.001*[1:N]))
s3=rvar2*square(2*π*(100*0.001*[1:N]))
s4=rvar1*cos(2*π*(150*0.01*[1:N]))
所加源信號如圖4所示。
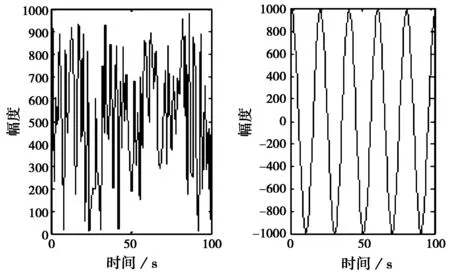
(a) 期望信號s1 (b) 干擾信號s2

(c) 干擾信號s3 (d) 期望信號s4圖4 四路源信號
圖5為MUSIC算法所測得的信號DOA,由圖5可以看出,該算法對四個源信號來波方向的估計都很精確,分辨率很高。并且譜峰強度是隨著信噪比的增大而增強的,仿真中假設信噪比30 dB時,譜峰強度可以達到104數量級。

圖5 MUSIC空間譜
圖6為源信號加到圓陣后所形成的混合信號,圖中七種不同線條符號的波形分別對應七個陣元上所接收到的信號。利用FastICA算法從圖5所示的混合信號中提取源信號,結果如圖7所示。
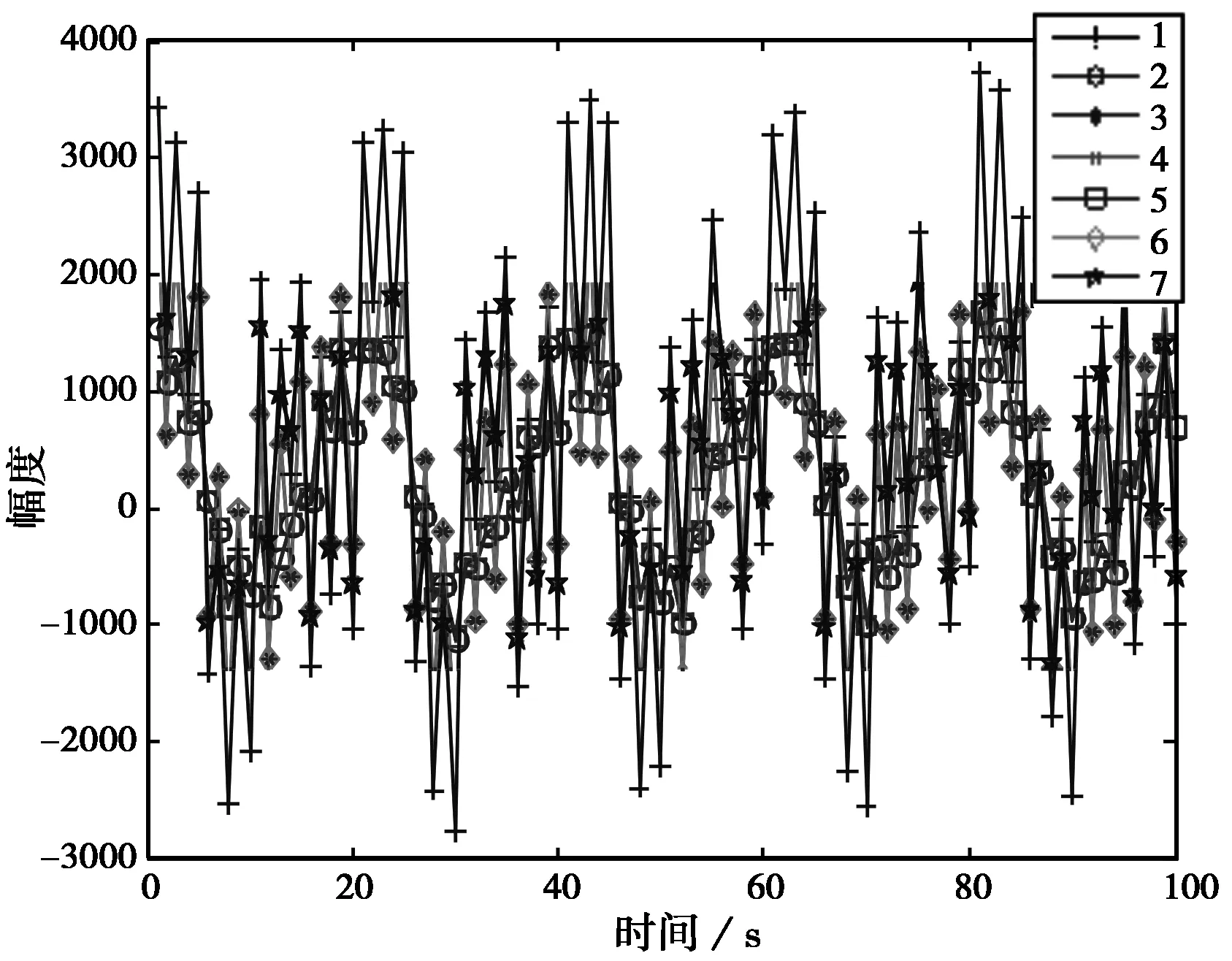
圖6 混合信號

(a) 分離結果1 (b) 分離結果2
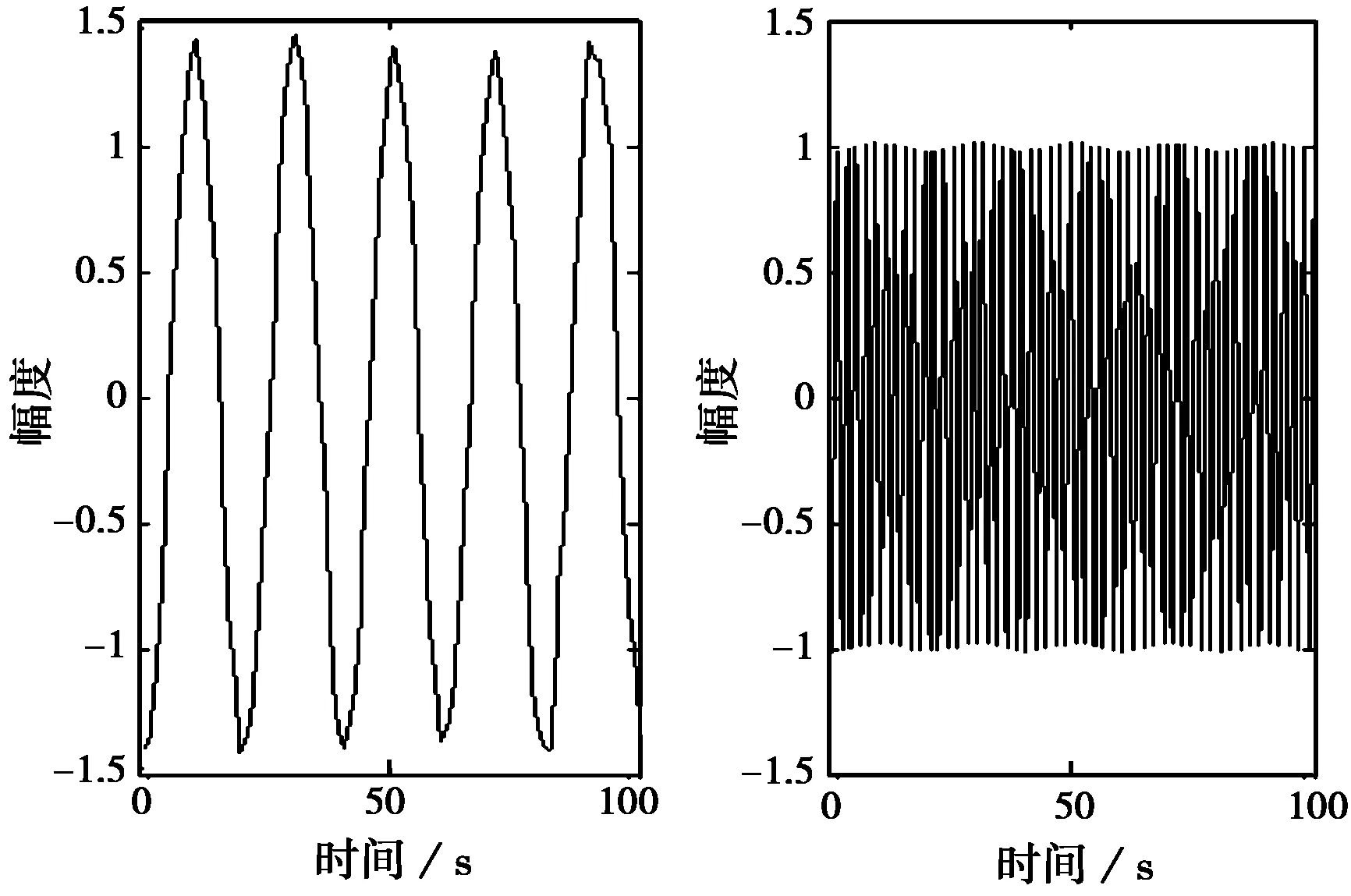
(c) 分離結果3 (d) 分離結果4圖7 FastICA算法的分離結果
將圖7所示的分離結果與圖4的源信號對比得:除了順序和幅度大小有所不同,這兩幅圖很相似,這說明FastICA算法的分離結果很接近源信號。同時由圖7可以看出,每個結果圖與原圖的幅度都相差很大,尤其是圖(b)所對應的隨機信號幅度。導致這種結果主要是由ICA算法存在2個內在的不確定性導致的[17]:1)輸出向量排列順序的不確定性,即無法確定所提取的信號對應的原始信號;2)輸出信號幅度的不確定性,即無法恢復到原信號的真實幅度。但由于主要信息都包含在輸出信號中,這兩種不確定性并不影響其應用。
利用最小均方差準則將分離信號與DOA對應后,采用MVDR算法在干擾的方位角處形成零陷,如圖8所示。
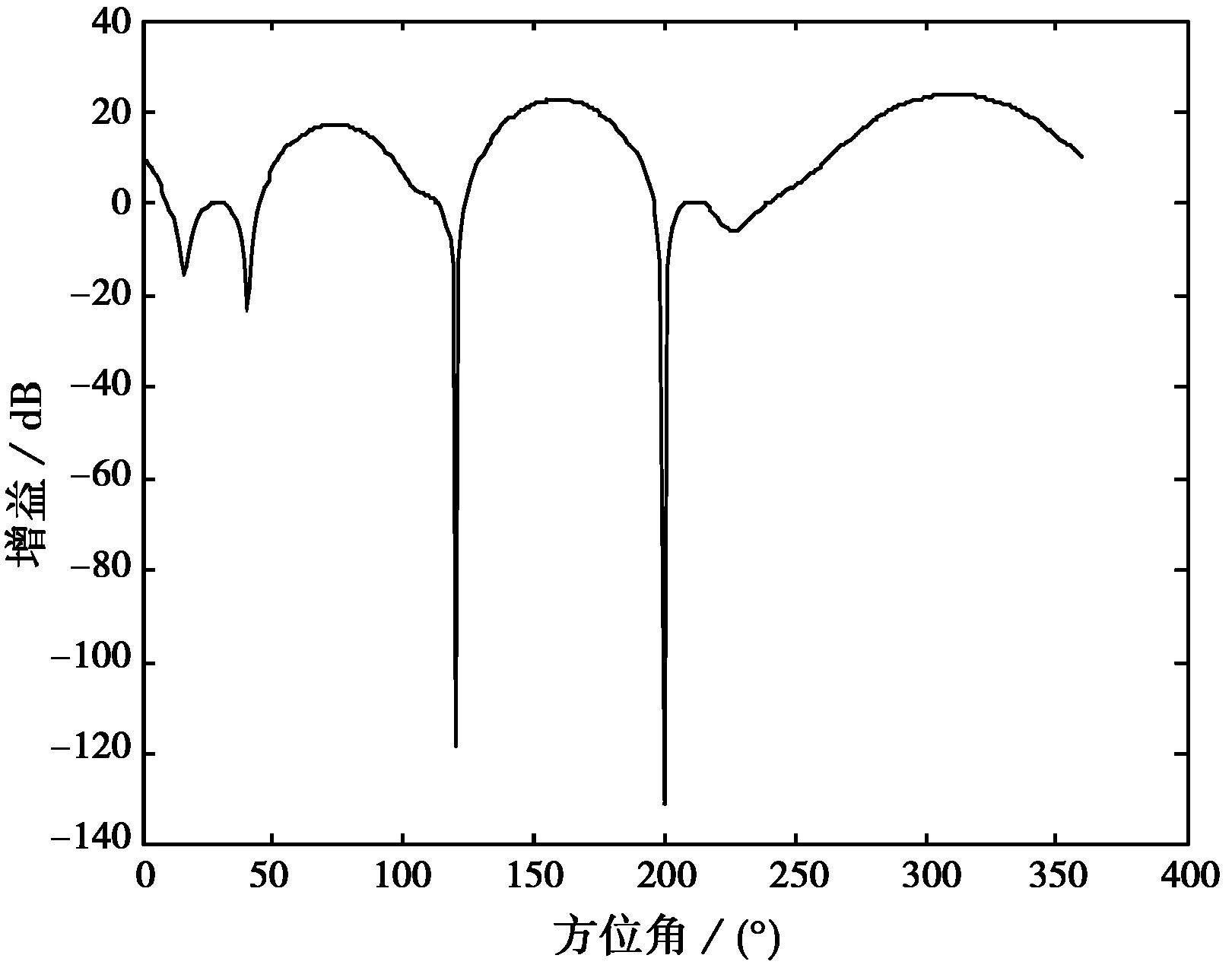
圖8 干擾零陷圖
從圖8可以看出,MVDR算法可以很好地在不希望的方向處形成較深的零陷,但同時卻在非干擾的方位處也形成了20 dB左右的零陷。這就說明:該算法雖然在某種程度上可以滿足系統要求,但同時仍需進一步改善,盡可能地使其在非干擾方位處所形成的零陷消失。
5. 結 論
文章基于均勻圓陣,提出一種基于盲源分離的自適應抗干擾方法,該方法能在干擾信號與期望信號比擬的情況下有效地抑制干擾,為導航系統抗弱干擾提供了新的思路。計算機仿真結果表明:該方法可以在與有用信號比擬的干擾處形成較深零陷,滿足衛星導航系統抗干擾的需求。
[1] 朱 莉,張國權,王光明. 基于均勻圓陣相干信源DOA估計的改進MUSIC算法[J]. 上海航天, 2009, 26(1): 31-33.
ZHU Li, ZHANG Guoquan, WANG Guangming. DOA estimation of coherent signals based on UCA with improved MUSIC algorthm[J]. Journal of Shanghai Aerospace, 2009, 26(1): 31-33. (in Chinese)
[2] SMON H. A daptive Filter Theory[M]. 北京:北京航空航天大學出版社, 2003.
SMON H. A daptive Filter Theory[M].Beijing: Beijing University of Aeronautics and Astronautics press, 2003. (in Chinese)
[3] SCH MIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE Trans on AP, 1986, 34(3): 276-280.
[4] ROY R, KAILATH T. ESPRIT-estimation of signal parameters via rotationl invariance techniques[J]. IEEE Trans on ASSP, 1989, 37(7): 984-995.
[5] 武思軍. 穩健的自適應波束形成算法研究[D]. 哈爾濱工程大學, 2005.
WU Sijun. The Study of Robust Adaptive Beamforming Algorithms[D]. Harbin Engineering University, 2005. (in Chinese)
[6] 鄭 洪. MUSIC算法與波達方向估計研究[D]. 四川大學, 2005.
ZHENG Hong. Study on MUSIC and DOA Estimation Algorithm[D]. Sichuan University,2005. (in Chinese)
[7] 楊 鵬, 楊 峰, 聶在平, 等. MUSIC算法在柱面共形天線陣DOA估計中的應用研究[J]. 電波科學學報, 2008, 23(2): 288-291.
YANG Peng, YANG Feng, NIE Zaiping, et al. DOA estimation of cylindrical conformal array by MUSIC[J]. Chinese Journal of Radio Science, 2008, 23(2): 288-291. (in Chinese)
[8] 張賢達, 保 錚. 通信信號處理[M]. 1版. 北京: 國防工業出版社, 2000.
ZHANG Xianda, BAO Zheng. Communication Signal Processing[M]. 1st ed. Beijing. National Defence Industry Press, 2000. (in Chinese)
[9] 余志斌, 金煒東, 張葛祥. 基于峰度的盲源分離算法研究與應用[J]. 電波科學學報, 2008,23(1): 146-152.
YU Zhibin, JIN Weidong, ZHANG Gexiang. Research and applications of blind signal separation based on kurtosis[J]. Chinese Journal of Radio Science, 2008, 23(1): 146-152. (in Chinese)
[10] 任光龍, 李鴻燕. 基于小波變換和FASTICA算法的有噪混合圖像盲分離[J]. 太原理工大學學報, 2009, 40(3): 229-231+239.
REN Guang-long, Li Hongyan. The Separation of Noisy Mixed Image Based on Wavelet Transform and Independent Component Analysis[J]. Journal of Taiyuan University of Technology. 2009, 40(3): 229-231+239. (in Chinese)
[11] HYVARINEN A, OJA E. A fast fixrd-point algorithm for independent component anlysis[J]. Neural Computation, 1997, 9(7): 1483-1492.
[12] 黃麗妍, 高 強, 亢海燕, 等. 改進的快速獨立分量分析算法[J]. 華北電力大學學報, 2006, 33(3): 59-62.
HUANG Liyan, GAO Qiang, KANG Haiyan, et al. Improved fastICA algorthm[J]. Journal of North China Electric Power University, 2006, 33(3): 59-62. (in Chinese)
[13] 孫正鼐, 肖 芳, 張 虹. 一種基于FastICA的波達方向估計新方法[J]. 計算機應用, 2006, 27(6): 1509-1512.
SUN Zhengnai, XIAO Fang, ZHANG Hong. New method for estimation of DOA based on FastICA[J]. Journal of computer application, 2006, 27(6): 1509-1512. (in Chinese)
[14] 王麗娜, 王 兵, 周賢偉. 一種新的智能天線波束形成算法[J]. 電波科學學報, 2007, 22(2): 351-354.
WANG Lina, WANG Bing, ZHOU Xianwei. A novel beamforming algorithm of smart antenna[J]. Chinese Journal of Radio Science,2007,22(2): 351-354. (in Chinese)
[15] 王 健, 惠曉威. DOA估計中MVDR算法的研究與實現[J]. 科技信息, 2007, 26(35): 84-85.
WANG Jian, HUI Xiaowei. The study and implementation of MVDR algorithm in DOA estimation[J]. Science Technology Information , 2007,26(35):84-85. (in Chinese)
[16] 莊學彬, 崔曉偉, 陸明泉, 等. 干擾環境下用于GPS接收機的波束形成算法分析[J]. 系統工程與電子技術, 2009, 31(3): 570-574.
ZHUANG Xuebin, CUI Xiaowei, LU Mingquan, et al. Analysis of beamforming algorithms for GPS receivers in the jamming environment[J]. Systems Engineering and Electronics, 2009, 31 (3): 570-574. (in Chinese)
[17] 張 念, 劉天佑, 李 杰. FastICA算法及其在地震信號去噪中的應用[J].計算機應用研究, 2009, 26(4): 1432-1434.
ZHANG Nian, LIU Tianyou, LI Jie. FastICA algorithm and its application in seismic signal noise elimination[J]. Application Research Of Computers, 2009, 26(4): 1432-1434. (in Chinese)

