基于損傷力學闡釋Manson－Coffin低周疲勞模型

鄭戰光 蔡敢為 李兆軍 徐細勇

廣西大學，南寧，530004

0 引言

19世紀60年代，Manson和Coffin在研究金屬材料疲勞的過程中注意到，當利用塑性應變幅εpa的對數與疲勞載荷反向次數2 Nf的對數進行作圖時，存在直線關系。于是他們提出了一種以塑性應變幅為參量的疲勞壽命描述法［1］，即

式中，m為疲勞延性指數；C為疲勞延性系數；Nf為以反向計數的疲勞壽命。

這就是著名的Manson－Coffin低周疲勞模型。它是建立在大量低周疲勞試驗數據基礎上的一個經驗公式；同時，疲勞延性系數與疲勞延性指數也均是Manson－Coffin公式擬合試驗數據的結果。因此，不僅無法解釋其力學含義，而且還需要大量的疲勞試驗數據。

低周疲勞破壞是工程結構中常見的一種失效形式。疲勞失效先在最不利的薄弱晶粒或夾雜等缺陷處發生損傷積累而演化，是一個能量耗散的過程。疲勞破壞的物理本質與損傷力學基礎理論是一致的。因此，本文旨在損傷力學的基礎上，推導建立低周疲勞壽命預測模型，并揭示Manson－Coffin公式所包含的力學意義。

1 基于損傷力學的低周疲勞損傷模型

1．1 損傷力學基礎理論

由于疲勞失效過程伴隨著熱量的產生與熱量的流動，而并非僅僅涉及機械能的轉換，同時在該過程中所發生的介質劣化與塑性應變均具有不可逆性，所以疲勞失效就屬于不可逆的熱力學過程。因此，由熱力學第二定律得出的Clausius－Duha mel不等式可得［2］：

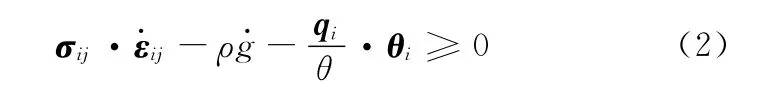
式中，σij、εij分別為Cauchy應力與無窮小應變張量；ρ為質量密度；g為單位質量的Hel mholtz自由能；qi為熱流密度矢量；θ為絕對溫度；θi為溫度梯度。

對于一個等溫的小變形過程，材料的局部熵產生的不等式（2）可以簡化為［3］

式中，ψ為單位體積的Hel mholtz比自由能。

材料在損傷過程中可以采用細觀定義的標量損傷變量D來描述材料的細觀損傷，那么Hel mholtz比自由能ψ是與應變和損傷有關的［4］，即

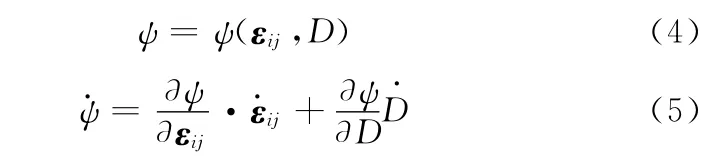
將式（5）代入式（3），可得

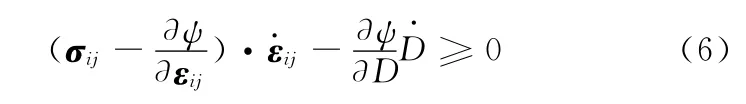
損傷過程是一個能量耗散過程，而耗散特性也可用另一個被稱為耗散勢或損傷流動勢的熱力學勢ψ＊來描述，它是關于體積能密度Y的凸函數，并由熱力學的對偶關系可得［5］

同時，由內變量的正交流動法則可得

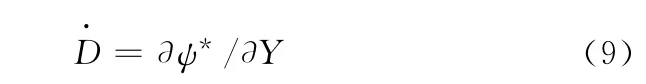
由式（9）可知，一旦給出了耗散勢就可以得到損傷演化方程。

1．2 延性損傷模型

為了推導損傷演化方程，基于式（9）并參考文獻［6］給出的耗散勢ψ＊，可將其表示為［6］

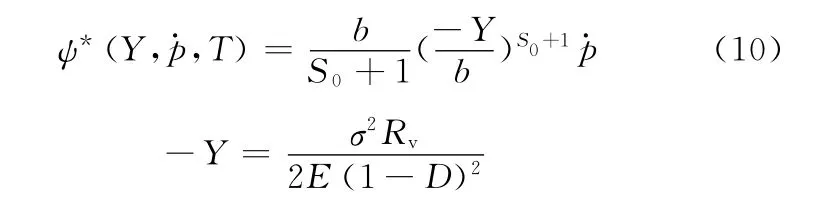
式中，Rv為三軸應力比；E為彈性模量；S0、b為材料常數；p·為累積塑性應變率。

將式（10）代入式（9）可得

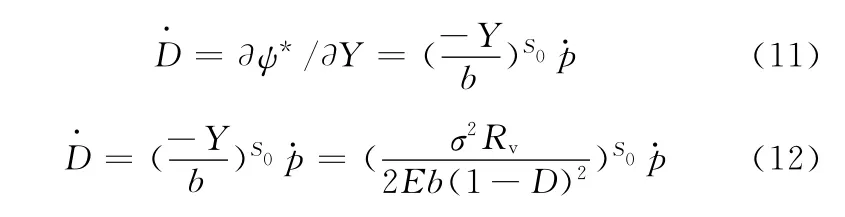
由損傷力學的有效應力概念［7］，可得

將式（13）代入式（12）可得在單調載荷作用下推導的延性損傷力學模型：

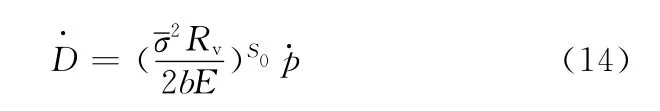
1．3 低周疲勞的損傷力學模型

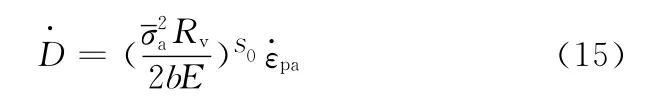
由于低周疲勞是以塑性應變幅為控制變量，同時，在塑性應變循環載荷作用下，金屬材料一般遵循Ramberg－Osgood冪率強化準則，因此，含損傷金屬材料應變疲勞的循環應力－應變行為可描述為［9］

式中，K為材料循環強度系數；n為材料循環應變硬化指數。

將式（16）代入式（15）可得

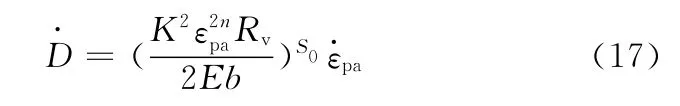
對一個循環的損傷進行計算：

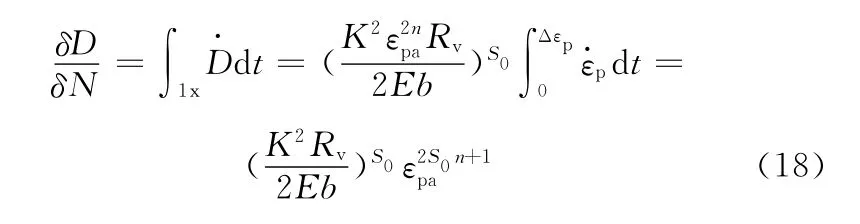
式中，1x表示一個循環。

在恒幅應變循環載荷作用下，整個疲勞損傷過程中的εpa是一個常量，則損傷D與疲勞壽命N之間的關系為

當疲勞損傷累積到D＝1時，其相應的疲勞壽命Nf可表示為

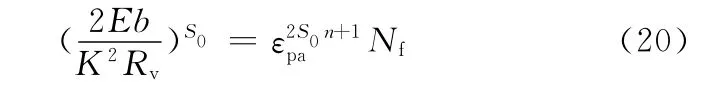
比較式（1）與式（20），如果要使兩式等價，就應該滿足條件：

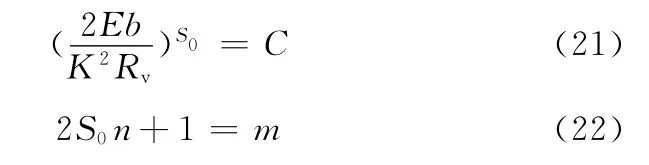
2 討論

如果要使式（21）成立，就必須使三軸應力比Rv為常數。這是因為式（21）中的系數E、K、C、b、S0均為常數，而三軸應力比Rv與加載方式有關，是一個不確定值。由文獻［2］可知：只有在比例加載的情況下，三軸應力比Rv才是常數，方能滿足式（21）成立的條件。這就證實了 Manson－Coffin公式是假設疲勞試樣在承受單軸載荷的條件下所提出來的。由此分析可得：Manson－Coffin公式僅僅是低周疲勞損傷力學模型在一定條件下的一種退化形式。

在Manson－Coffin低周疲勞模型中，材料的疲勞延性系數C由相應的疲勞試驗進行確定，由此可見，它是一個經驗值，缺乏明確的物理含義。假如式（21）成立的話，那么疲勞延性系數C就有自己的表達式，它不僅與彈性模量E、材料循環強度系數K和材料常數b、S0有關，還跟反映加載方式的三軸應力比Rv有關。因此，損傷力學模型不僅具有豐富的物理內涵，而且其參數的確定也無需大量試驗參數來擬合。

至于式（22），由于系數m、n、S0均為常數，為了實現式（1）與式（20）之間的相互溝通，式（22）是可以恒成立的。在Manson－Coffin公式中，材料的疲勞延性指數m是通過疲勞試驗確定的，而式（22）卻充分表達了疲勞延性指數m的含義，它再不是一個孤立的常數，而是與材料的循環應變硬化指數n和材料常數S0的乘積有關的數。

3 結論

（1）傳統的疲勞經驗公式可由損傷力學的理論導出，由此賦予了疲勞經驗公式在損傷力學意義下的解釋，使得疲勞經驗公式有了明確的物理內涵。

（2）給出了Manson－Coffin公式與低周疲勞損傷力學模型的等價條件。在比例加載的情況下，低周疲勞損傷力學模型可退化為Manson－Coffin公式，從而進一步驗證了低周疲勞Manson－Coffin公式適用于比例加載的理想條件。

（3）探明了Manson－Coffin公式中的疲勞延性系數與疲勞延性指數分別與低周疲勞損傷力學模型中的各常數之間的關系。通過損傷力學推導，不僅使Manson－Coffin公式具有豐富的物理內涵，而且其參數也僅需要少量的力學性能試驗就可以確定。

［1］ Manson S S．Fatigue：A Co mplex Subject So me Simple approximations［J］．J．of Experiment Mechanics，1965，5（7）：193－226．

［2］ Lemaitre J．A Course on Damage Mechanics［M］．Berlin：Springer－Verlag，1992．

［3］ 唐雪松，鄭健龍，蔣持平．連續損傷理論與應用［M］．北京：人民交通出版社，2005．

［4］ Chaboche J L，Lesne P M A．Linear Continuous Fatigue Damage Model［J］．Fait．Engnt．Mater．Struct，1988，11（1）：1－17．

［5］ Dattoma V，Giancane S，Nobile R，et al．Fatigue Life Prediction Under Variable Loading Based on a New Non－linear Continuu m Damage Mechanics Model［J］．Inter national Jour nal of Fatigue，2006，28（1）：89－95．

［6］ Chandrakanth S，Pandey P C．An Isotropic Damage Model f or Ductile Material［J］．Engineering Fracture Mechanics，1995，50（4）：457－465．

［7］ Yang X H，Li N，Jin Z H，et al．A Continuous Low Cycle Fatigue Damage Model and Its Application in Engineering Materials［J］．Int．J．Fatigue，1997，19（10）：687－692．

［8］ 荊建平，夏松波，孫毅，等．汽輪機轉子結構強度理論研究現狀與展望［J］．中國機械工程，2001，12（增刊1）：216－219．

［9］ Kunc R，Prebil I．Low－cycle Fatigue Properties of Steel 42Cr Mo4［J］．Materials Science and Engineering，2003，A（345）：278－285．