高鐵軌道基準網平面網坐標轉換方法研究＊

鐘昊然，劉成龍，付恒友，楊雪峰，陳海軍

(1.西南交通大學地球科學與環境工程學院，四川成都 610031;2.滬昆鐵路客運專線浙江有限責任公司，浙江杭州 310009)

高鐵軌道基準網平面網坐標轉換方法研究＊

鐘昊然1，劉成龍1，付恒友2，楊雪峰1，陳海軍1

(1.西南交通大學地球科學與環境工程學院，四川成都 610031;2.滬昆鐵路客運專線浙江有限責任公司，浙江杭州 310009)

在高速鐵路軌道基準網平面網數據處理中，需要將外業所測合格的軌道基準點坐標從測站站心坐標系轉換到鐵路工程獨立坐標系，目前德國采用的是三參數坐標轉換模型，而不是常規采用的四參數坐標轉換模型。介紹了2種平面坐標轉換模型及其轉換參數精度評定的算法，通過對2種坐標轉換的轉換參數精度、坐標轉換前后公共點殘差以及站間坐標搭接情況的比較分析，認為2種坐標轉換方法均能滿足軌道基準網的精度要求，但是在其上一級CPⅢ控制網為約束平差的前提下，采用四參數坐標轉換方法效果更優。

坐標轉換;三參數;四參數;轉換參數精度;軌道基準網

目前，世界高速鐵路大多采用無砟軌道技術。博格板式無砟軌道系統是我國引進的一種無砟軌道結構形式，經過消化、吸收、再創新，形成中國特色的板式無砟軌道，稱為Ⅱ型板式無砟軌道技術［1］。在高速鐵路精密工程測量領域，博格無砟軌道系統與其他軌道系統的重要區別之一，是在軌道控制網CPⅢ下多了一級加密控制網，我國目前稱之為軌道基準網(以下簡稱為TRN)。TRN為三維網，包括TRN平面網和TRN高程網，其主要作用是作為軌道板精調施工測量控制的基準［2］。

TRN外業測量完成后，就要進行TRN平面網的數據處理，其主要原理為:先站內處理，再站間搭接。其中站內處理就是以本測站聯測的CPⅢ控制點在測站站心坐標系中多次觀測的坐標均值作為觀測值，結合各CPⅢ控制點在鐵路工程獨立坐標系中的已知坐標，以間接平差的方法求解測站站心坐標系和鐵路工程獨立坐標系間的坐標轉換參數，再根據得到的坐標轉換參數，將測站站心坐標系中各軌道基準點(以下簡稱TRP)的坐標均值進行坐標轉換，從而得到各TRP在鐵路工程獨立坐標系中的坐標［3］。目前的高速鐵路建設工程實踐中，對于TRN平面網站內數據處理，德國是采用三參數坐標轉換模型，即不顧及鐵路工程獨立坐標系和TRN測量時站心坐標系間存在的尺度差異;而國內部分客運專線采用的是四參數坐標轉換模型，即將傳統的約束平差理念運用于TRN平面網與其上一級控制網CPIII平面網［4］。眾所周知，二維平面坐標轉換有三參數和四參數2種模型，選擇不同的坐標轉換模型進行TRN平面網的站內數據處理，是否會對TRN平面網的坐標結果及其精度產生影響，是本文研究的主要問題。

本文介紹了2種坐標轉換的模型及其轉換參數精度的評定方法，在此基礎上，對二者應用在TRN平面網站內數據處理時的公共點殘差、轉換參數的精度、測站間搭接點縱橫向坐標較差進行對比和統計分析，從而為TRN平面網站內數據處理究竟采用哪種坐標轉換模型提供參考。

1 2種平面坐標轉換方法原理

1.1 三參數坐標轉換模型

由于不考慮CPⅢ控制網和TRN測量站心坐標系的尺度差異，德國采用三參數坐標轉換，以下為其坐標轉換原理。設各CPⅢ控制點在本測站站心坐標系中的坐標為(x0，y0)CPIII，在鐵路工程獨立坐標系中的已知坐標為(x，y)CPIII，則三參數坐標轉換模型為:

1.2 四參數坐標轉換模型

若要考慮CPⅢ控制網和TRN測量站心坐標系的尺度差異，2套平面坐標系間應采用如下四參數的坐標轉換模型，即:

式中，Δx，Δy和α分別為2套坐標系間的平移參數和旋轉參數。

將上式中的Δx，Δy和α作為平差參數，對獨立坐標系下的CPⅢ坐標可開列如下的誤差方程式:

式中，Δxo，Δyo和αo為平差參數的近似值。

TRN平面網坐標測量時，CPⅢ公共點的個數一般大于4，則可根據最小二乘原理，在滿足VTV=min的原則下進行參數估計，可求得坐標轉換參數Δx，Δy和α的最佳估值，再利用下面的三參數坐標轉換模型，即可將各TRP在本測站站心坐標系中的坐標(x0，y0)TRP，轉換成鐵路工程獨立坐標系中的坐標 (x，y)TRP。

式中，Δx，Δy，k和 α分別為2套坐標系間的平移參數、尺度參數和旋轉參數。

將上式中的 Δx，Δy，k和 α 作為平差參數，對獨立坐標系下的CPⅢ坐標可開列如下的誤差方程式:

式中，Δxo，Δyo，ko和 αo為各平差參數的近似值。

同理，可根據公共點的2套坐標采用平差的方法求得坐標轉換參數Δx，Δy，ko和α的最佳估值，并利用這些參數的最佳估值按下面的四參數坐標轉換模型，將各TRP在本測站站心坐標系中的坐標(x0，y0)TRP，轉換成鐵路工程獨立坐標系中的坐標 (x，y)TRP。

1.3 坐標轉換參數精度的評定方法

對TRN平面網數據處理而言，轉換參數的精度是衡量哪種坐標轉換方法效果更優的參數之一。下面介紹四參數坐標轉換的轉換參數精度評定的方法。

由于在系數矩陣2nB×4中含有轉換參數的近似值，所以首先要根據公共點轉換前后的坐標計算轉換參數的近似值。對于平移參數，取轉換前后2套坐標的均值即可得到轉換前后公共點的重心坐標，再將轉換前后公共點重心坐標之x和y坐標分別相減即可得出平移參數的近似值Δxo和Δyo;對于旋轉參數，公共點中某條固定邊轉換前后坐標方位角的差值，即為旋轉角α的近似值αo;對于尺度因子，在轉換前后兩坐標系中，分別取相同兩公共點坐標反算出兩點間距離，再將兩距離相比即可得到尺度因子k的近似值ko。以上就得到了4個坐標轉換參數的近似值，亦即確定了系數矩陣。

根據式(13)的誤差方程，按間接平差原理［4］組成法方程:

將上式求出的^x代入(13)式中，可求得改正數:

據此可按下式計算坐標轉換的單位權中誤差:

根據間接平差的原理，平差參數的協因數陣為:

取協因數陣對角線元素QδΔxδΔx，QδΔyδΔy，QδΔkδΔk和QδΔαδΔα，可按下式計算轉換參數的中誤差:

同理，可根據以上所述的類似方法計算三參數坐標轉換的轉換參數中誤差。

2 2種坐標轉換結果的比較

2.1 CPⅢ控制點坐標殘差比較

為了驗證坐標轉換參數求解的正確性和各CPⅢ控制點的精度和穩定性，可利用平差后得到的坐標轉換參數，按坐標轉換公式(1)或(7)，對各CPⅢ點的本測站站心坐標系中的坐標均值進行坐標轉換。若轉換后大多數CPⅢ點(至少有4個點)的X和Y坐標與已知CPⅢ點的X和Y坐標的差值在2 mm以內，則所求的坐標轉換參數合格，否則應剔除坐標轉換后X和Y坐標差值大于2 mm的CPⅢ點(可視該CPⅢ點為不穩定點或精度不滿足要求的點)，并重新平差計算求解坐標轉換參數，直到所求的坐標轉換參數合格［6］。表1為某客運專線465個CPⅢ控制點，通過2種坐標轉換方法后坐標殘差的統計情況。

表1 CPⅢ控制點坐標殘差統計結果Table 1 The statistics result of CPIII control point’s coordinate residuals

在所統計的465個CPⅢ點中，絕大部分CPⅢ點的X和Y坐標與已知CPⅢ點的X和Y坐標的差值在2 mm以內，說明兩種方法所求的轉換參數均合格。通過表1還可知，四參數坐標轉換后，X和Y坐標殘差超過2 mm的點個數和各CPⅢ控制點的坐標殘差明顯小于三參數坐標轉換。

2.2 轉換參數精度的比較

2.2.1 轉換參數精度實測數據比較

在某客運專線TRN平面網外業測量數據中，根據上述2種轉換參數計算模型，計算了64個測站的轉換參數精度。由于三參數坐標轉換的轉換參數中，不含有尺度因子k，因此在轉換參數精度實測數據比較時，只統計共有的平移參數和旋轉參數的中誤差，統計結果見表2。

表2 2種轉換方法中誤差計算統計結果Table 2 The statistics result of two transform method’s mean square error

由表2可以看出，2種坐標轉換方法的平移參數精度相差甚小，但是四參數坐標轉換的旋轉參數精度明顯高于三參數坐標轉換。

2.2.2 2種坐標轉換參數精度的離散性分析

由于2種坐標轉換方法的轉換參數精度相差較小，為了進一步區分2種坐標轉換方法轉換參數精度的差異，計算了64個測站的轉換參數中誤差的中誤差［7］，由此可分析兩種坐標轉換方法的轉換參數中誤差的離散性，計算的統計結果見表3。

表3 2種坐標轉換參數中誤差的中誤差統計結果Table 3 The statistics result of two transform method’s mean square error’s mean square error

由表3可以看出，三參數坐標轉換的平移參數及旋轉參數中誤差的中誤差均大于四參數坐標轉換，由此可以認為，四參數坐標轉換的轉換參數精度離散性更小，穩定程度優于三參數坐標轉換。

2.3 測站間搭接TRP坐標較差的比較

前已述及，TRN平面網數據處理包括站內坐標轉換和站間坐標搭接。衡量站間坐標搭接效果好壞的質量指標是搭接點的縱、橫向坐標差值。表4是4952個搭接點三參數和四參數坐標轉換后搭接點坐標較差的統計結果。

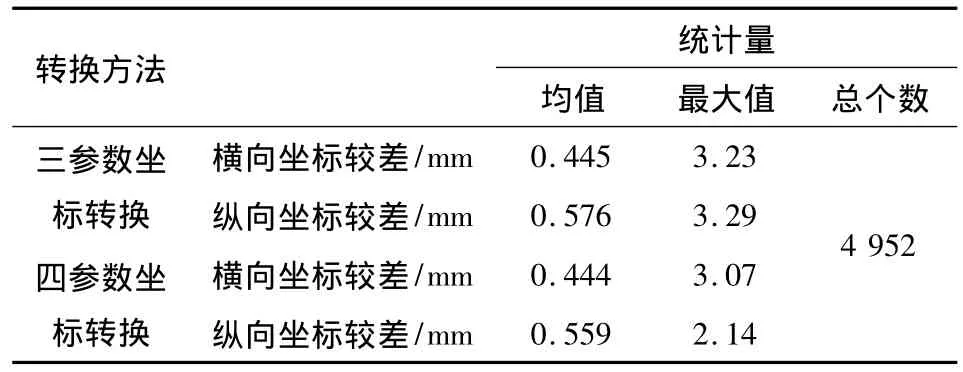
表4 2種坐標轉換后搭接點的縱橫向坐標較差(絕對值)統計表Table 4 The statistics result of two transform method’s lap point’s coordinates(absolute)

由表4可以看出，4 952個搭接點的縱、橫向坐標差值統計數據中，四參數坐標轉換后橫向坐標差值均值小于三參數坐標轉換后橫向坐標差值均值，四參數坐標轉換后縱向坐標差值均值也小于三參數坐標轉換后縱向坐標差值均值，且四參數坐標轉換后搭接點的縱、橫向坐標較差絕對值最大值，也均小于三參數坐標轉換后縱、橫向坐標較差絕對值的最大值。

3 結論

四參數坐標轉換通過尺度因子k的作用可以使得TRN和上一級CPⅢ控制網的尺度保持一致，但這會引起TRN網形的微小變化，且將上一級控制網的誤差帶入TRN;而三參數坐標轉換，不考慮CPⅢ控制網和TRN測量的尺度差異，保證了TRN網形不會發生變化，但是由于TRN和CPⅢ控制網尺度不一致，在控制坐標轉換前后公共點坐標殘差方面效果欠佳。

經過對實測數據的統計和比較分析后，發現2種坐標轉換方法均能達到目前TRN測量精度的要求，但四參數坐標轉換在公共點殘差、轉換參數精度以及站間坐標搭接效果方面占有優勢，所以本文認為:TRN是在CPⅢ控制網基礎上的加密控制網，由于現階段CPⅢ控制網均采用約束平差，因此TRN平面網站內數據處理可以采用四參數坐標轉換，通過四參數中尺度因子的作用，使得TRN平面網在公共點殘差、轉換參數精度以及站間坐標搭接等方面效果更好，也符合上一級控制網的平差理念，因此認為我國的TRN平面網的坐標轉換應該采用四參數的坐標轉換方法。

［1］趙國堂.高速鐵路無砟軌道結構［M］.北京:中國鐵道出版社，2006:74－77.

ZHAO Guo－tang.High speed railway ballastless track structure［M］. Beijing:China Railway Publishing House，2006:74 －77.

［2］石德彬，王長進.高速鐵路無砟軌道基準網(CP4)測量和數據處理研究［C］//高速鐵路精密測量理論及測繪新技術應用國際學術研討會論文集.成都:西南交通大學出版社，2010.

SHI De-bin，WANG Chang-jin.Research on surveying and data processing for densification fiducial mark for tracklaying of ballastless track high－speed railway［C］//Proceedings of the International Symposium on Precision Engineering Survey Theory and Spatial Information Technology for High Speed Railway.Chengdu:Southwest Jiaotong University Press，2010.

［3］劉成龍，楊雪峰.高速鐵路軌道基準網數據采集與處理系統研發報告［R］.成都:西南交通大學，2010.

LIU Cheng-long.YANG Xue-feng.Report on research and development of track reference network data measurement and processing system for high speed railway［R］.Chengdu:Southwest Jiaotong University，2010.

［4］陳海軍，劉成龍，付恒友.高速鐵路軌道基準網平面網構網測量及嚴密平差方法研究［J］.鐵道科學與工程學報，2011，8(4):55－60.

CHEN Hai-jun，LIU Cheng-long，FU Heng-you.Research on the network－constructed measurement and strict adjustment methods in the plane network of Track Reference Network in high － speed railway［J］.Journal of Railway Science and Engineering，2011，8(4):55 －60.

［5］武漢大學測繪學院，測量平差學科組.誤差理論與測量平差基礎［M］.武漢:武漢大學出版社，2003.

Subject Group of Surveying Adjustment，School of geodesy and geomatics.Wuhan University.Theory of Errors and Basis of Surveying Adjustment［M］.Wuhan:Wuhan U-niversity Press，2003.

［6］何 平.數理統計與多元統計［M］.成都:西南交通大學出版社，2004.

HE Ping.Mathematical statistics and multivariate statistics［M］.Chengdu:Southwest Jiaotong University Press，2004.

［7］王 鵬，劉成龍，楊 希.無碴軌道CPⅢ自由設站邊角交會網平差概略坐標計算方法研究［J］.鐵道勘察，2008(3):26－28.

WANG Peng，LIU Cheng-long，YANG Xi.Research on calculation methods of preliminary coordinates for adjustment in ballastless track base－piles control pointsⅢwith free station linear angular intersection［J］.Railway Investigation and Surveying，2008(3):26－28.

Track baseline data processing network method for coordinate transformation in high－speed railway

ZHONG Hao-ran1，LIU Cheng-long1，FU Heng-you2，YANG Xue-feng1，Chen Hai-jun1

(1.Faculty of Geosciences and Environmental Engineering，Southwest Jiaotong University，Chengdu 610031，China;2.Shanghai－ Kunming Railway Passenger Zhejiang Company，Hangzhou 310009，China)

To process the data of horizontal network of track basis net of the high－speed railway，it is required to rewrite coordinates of qualified track datum mark，which are surveyed in the field operation，from the survey station’s topocentric coordinate system into the independent coordinate system of railway engineering.At status quo，Germany adopts tri－parameter transformation model rather than the regularly utilized quad－parameter transformation model.In this article，both coordinate systems and the algorithm of assessing the precision of the parameter transformation are introduced.It is suggested that both transformation models could meet with the requirements of precision of track basis net，through the comparative analysis on the transformation parameters’precision of both coordinate systems by the residual error of common points before and after the coordinate transformation，and the overlapping situations from various stations.However，it is quad－parameter coordinate transformation that appears to be better，on the assumption that the higher level，i.e.CPIII control network is used as the constrained surveying adjustment.

coordinate transformation;tri－parameter;quad－parameter;precision of parameter transformation;track basis net

P258

A

1672－7029(2011)06－0122－05

2011－10－25

西南交通大學專題研究項目資助(SWJTU10ZT02)

鐘昊然(1987－)，男，四川成都人，碩士研究生，從事精密工程測量與變形監測研究