曲線橋在地震作用下的面內轉動機理分析

黃明非

（重慶交通大學土木建筑學院，重慶 400074）

曲線橋在地震作用下的面內轉動機理分析

黃明非

（重慶交通大學土木建筑學院，重慶 400074）

曲線橋梁在水平地震作用下，上部結構在兩個主方向上的地震反應會產生耦合現象，該現象主要為梁端的橫向位移和橋面板的面內轉動;通過對簡化的單跨曲線橋模型進行彈性時程分析，研究曲線橋在弦線方向的地震輸入下的轉動機理，并比較不同曲率半徑下曲線橋的地震反應;討論主梁-橋臺相互作用對橋面板轉動的影響，應用非線性時程分析計算不同曲率的曲線橋在不同地震輸入角度下的地震反應，并確定最不利地震輸入角度。

曲線橋;地震反應;面內轉動;地震輸入角度

曲線橋由于自身的幾何特點，其靜力反應和動力反應均與直線橋梁存在較大差異。在重力作用下上部結構會發生彎扭耦合現象;在地震作用下除彎扭耦合現象加劇外，橋面板還會在兩個水平主方向上產生位移耦合，并伴隨橋面板的旋轉。“5.12”汶川地震中，大多數曲線橋上部結構發生了不同程度的永久性面內轉動位移。建于2004年的百花大橋為震區橋梁中結構受損最為嚴重、影響最為廣泛的橋梁之一。該橋為S型曲線連續梁橋，未倒塌的第2、4、6聯梁體發生了不同程度轉動，其中第6聯順時針轉動1.55°，為梁段中的最大轉動位移，所有梁體均存在嚴重的落梁風險。對該橋的震害調查說明橋面板在地震作用下有可能發生轉動位移，該位移會導致落梁風險。

雖然越來越多的國內外學者對曲線橋梁進行了抗震研究，并取得一定進展。但在最近幾次破壞力較大的地震中，曲線橋仍然出現較嚴重的震害，因此進一步研究曲線橋的地震反應特點是必要的。現階段國內外研究主要集中在上部結構的內力計算和下部結構的性能安全［1-4］，對于曲線橋橋面板轉動機理的研究相對較少。隨著隔振設計的推廣，要求上部結構擁有更大的位移能力［5］，因此上部結構位移性能應作為曲線橋動力分析和抗震設計的重點之一。

筆者僅研究曲線橋上部結構在地震作用下的面內轉動機理。討論了簡化條件下單跨曲線橋的轉動問題，通過線性動力分析說明了曲率半徑對轉動的影響。然后通過非線性時程分析，研究主梁-橋臺相互作用對上部結構轉動的影響。最后通過對一系列模型的計算，得出最不利地震輸入角度的一般規律。

1 彈性支承曲線橋梁的地震反應

1.1 計算模型和力學分析

跨徑不大的單跨曲線橋通常采用板式橡膠支座，其上部結構的剛度相對較大。忽略彎扭耦合效應后可將上部結構和支座系統簡化為線彈性支承的剛性板。如圖1，系統的廣義坐標取U1、U2和R3，其中U1方向為沿弦線方向、U2垂直于U1、R3為繞質心點A的轉動，以上廣義坐標決定了橋面板在面內的幾何位置。梁端i、j的支座反力作用點位于橋面板中線上。定義質心與弦線L的距離為偏心距e。

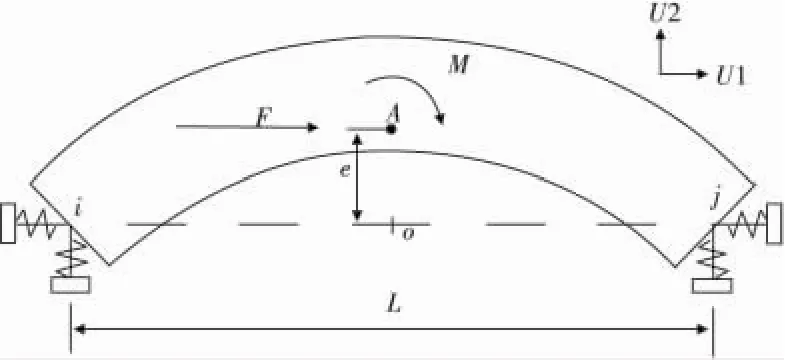
圖1 單跨曲線橋計算模型Fig.1 Calculation model of the single-span curve bridge

剛性板在平行于U1、且通過質心A的外力F作用下會產生沿該方向的位移，由力的平衡關系可得:

由于U2方向上未受力，所以質心在該方向上不會有位移產生。此外，由于A點與弦線L不重合，導致F將對割線中心點O產生力矩M。通過最小勢能原理分析可知，橋面板為保持平衡，必須產生R3位移，該轉動在i、j兩端支座處產生U2方向的反力 fi2和fj2。現設i、j兩端U2方向的支座剛度分別為 k2i、k2j，位移分別為 Δ2i和 Δ2j，由U2方向受力平衡可得:

由ΣM（O）=0可得:

對于均勻質量分布的圓弧形上部結構，e可用式（4）計算:

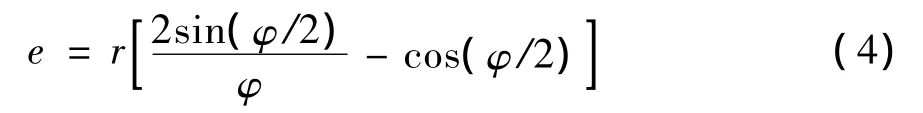
式中:φ為圓弧轉角;r為圓弧半徑。

而φ與弦線長度有以下關系:

綜合式（4）、式（5），偏心距e可表示為半徑r和弦線長度L的函數:

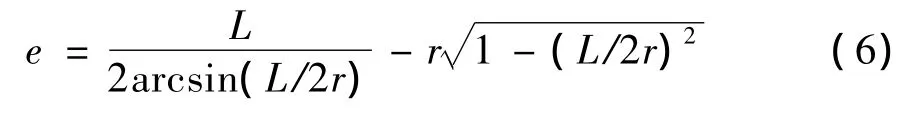
式（6）說明在弦線L一定的情況下，e隨r的增大而減小。利用公式（2）和公式（3）可以求得Δ2i和Δ2j，且 Δ2i、Δ2j不為 0，進而可確定橋面板的轉角。剛性曲線橋面板在受弦線方向上的外力作用時，橋面板的總體反應為弦線方向的平移和面內轉動的疊加。

1.2 線性時程分析

通過以上分析可知，曲線橋的自身幾何特性導致質心M與支座U1方向反力不在同一直線上，因而在地震作用下產生面內轉動。由公式（3）可看出，質心偏心距e對轉角的大小起控制作用。現運用Sap2000有限元軟件對單跨曲線橋進行線性動力時程分析，以驗證曲線橋的轉動機理，并研究曲率半徑對轉動的影響。該計算模型為圓弧曲線橋，跨長15 m（橋面中心線割線長度）;上部結構采用shell單元、通過施加節點束縛來模擬剛性板;橋梁僅在梁端受線彈性連支座約束，支座水平剛度k=4×105N/m;為簡化分析過程，采用峰值加速度為0.2 g、頻率為1Hz的簡諧地震波沿U1方向輸入，作用時間10 s;曲率半徑按 10，15，20，25，30 m 變化;各個模型的系統阻尼比設定為5%。模型概況見圖2。

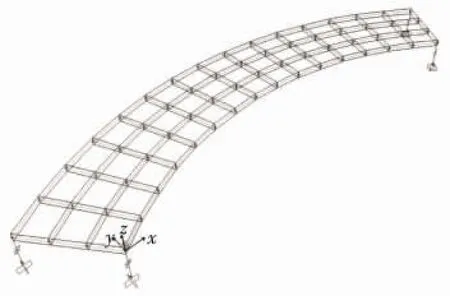
圖2 單跨曲線橋有限元模型Fig.2 Finite element model of single-span curve bridge

圖3為r=10 m時i端橋中線處的位移時程，顯示了曲線橋在弦線方向的地震作用下梁端處在2個主方向上發生了位移耦合，且橋面板發生轉動。

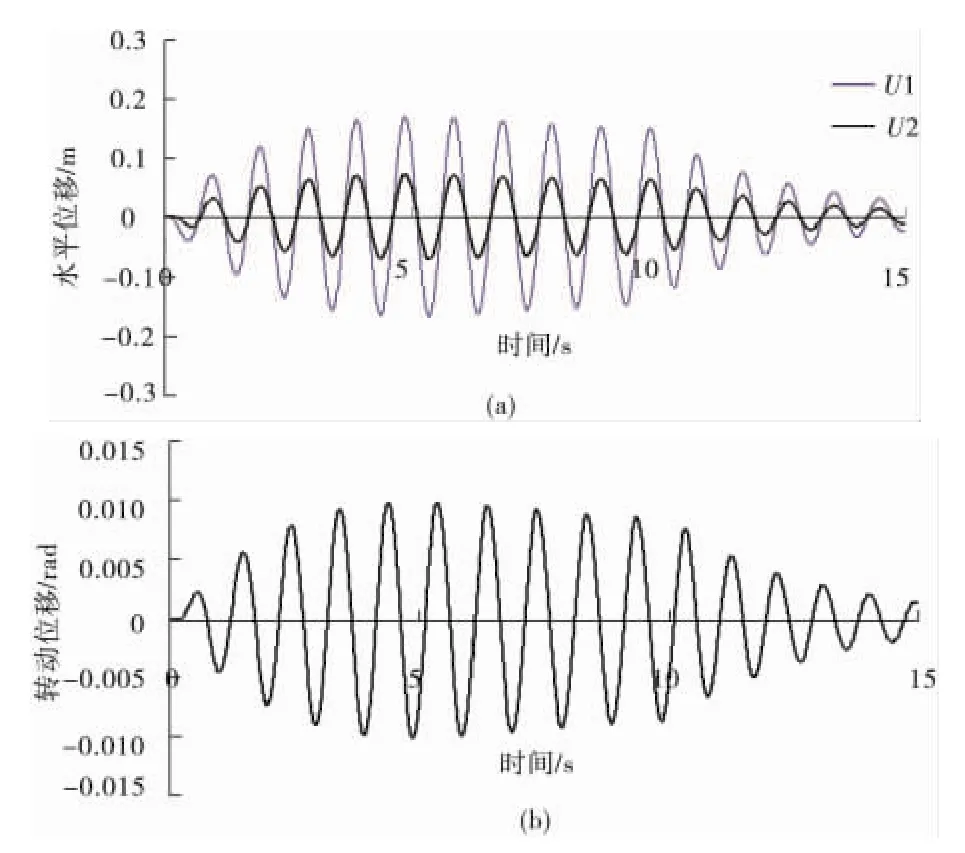
圖3 i端位移Fig.3 Displacement of i-end

由圖4可看出，曲線橋i、j端的U2向位移關于0點存在對稱關系，說明橋面板整體不會在U2向發生位移，橋面板的轉動是梁端處產生U2位移的原因。

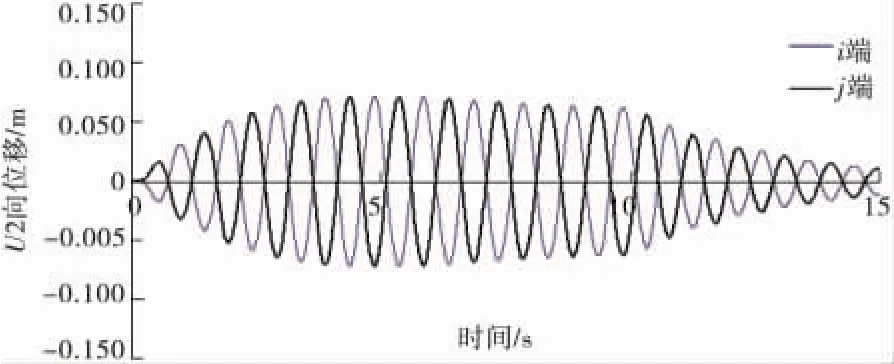
圖4 i端、j端位移Fig.4 Displacement of i-end and j-end

圖5顯示了不同曲率半徑下橋面板的地震反應。由圖可見，隨著r的增大，橋面板的轉動程度減小，梁端的橫向位移也隨之減小。實際情況下，水平地震波輸入方向不一定和弦線平行，對于線性分析可運用疊加原理將地震波分解為U1和U2方向分別輸入，其中U1方向的地震輸入會產生橋面板轉動，U2方向上支座反力關于質心對稱，不會導致R3位移。

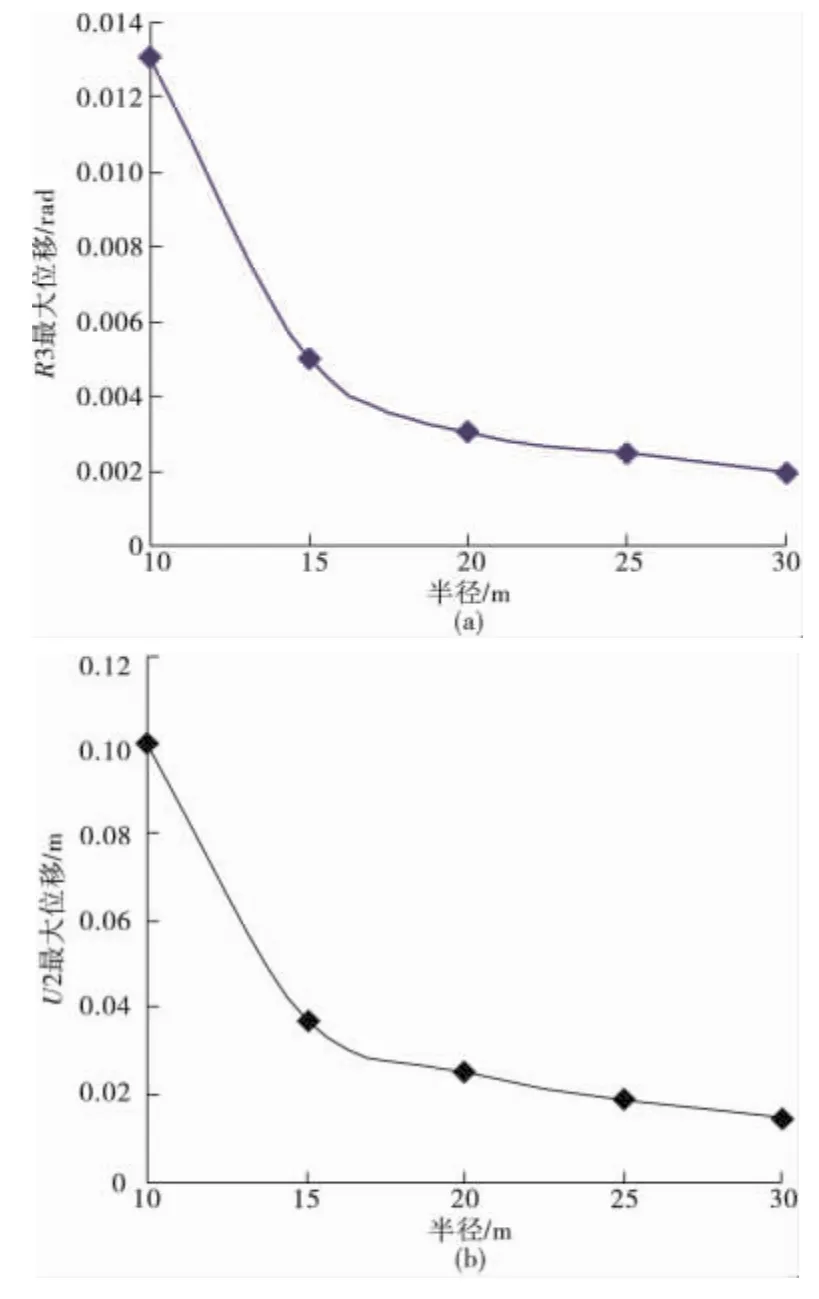
圖5 不同曲率半徑下的i端最大位移Fig.5 Displacement of i-end of different curvature

2 主梁-橋臺相互作用對地震反應的影響

2.1 主梁-橋臺相互作用計算方法

主梁-橋臺的相互作用主要表現為主梁和橋臺的碰撞，地震作用下上部結構水平位移過大時就可能與橋臺發生碰撞。目前國內外主要基于剛體碰撞理論進行橋梁碰撞問題的研究［6］，分別用等效的彈簧單元和縫單元來模擬碰撞過程中的相互作用和間隙。在此采用Sap2000中的GAP單元來模擬橋梁的伸縮縫，如圖6。

圖6 縫單元示意Fig.6 Gap element schematic diagram

梁與橋臺的碰撞計算可用式（7）表示:

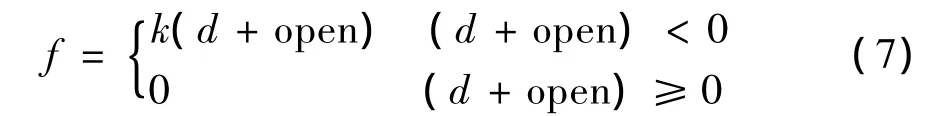
式中:k為彈簧剛度;open為初始縫開啟，在此為伸縮縫寬度。

2.2 主梁-橋臺相互作用下的地震反應

基于曲率半徑r=10 m，跨徑15 m的圓弧線曲線橋進行非線性動力時程分析，計入主梁-橋臺相互作用，在各個支座處設置水平GAP單元，假定撞擊力方向為沿梁端切線方向，伸縮縫的寬度設為0.1 m。彈簧剛度k由伸縮縫特性、橋臺剛度、主梁剛度、臺后填土等因素綜合決定，目前國內外對此研究尚無定論［5］。由于該值的取定不是本文研究的重點，基于汶川地震中橋臺受碰撞損害嚴重且橋臺自身剛度較大的事實，在此計算中取一較大值:k=5×107N/m。輸入地震作用為峰值加速度0.2 g、頻率1 Hz、沿U1方向的簡諧地震波，作用時間10 s。計算結果見圖7～圖9。

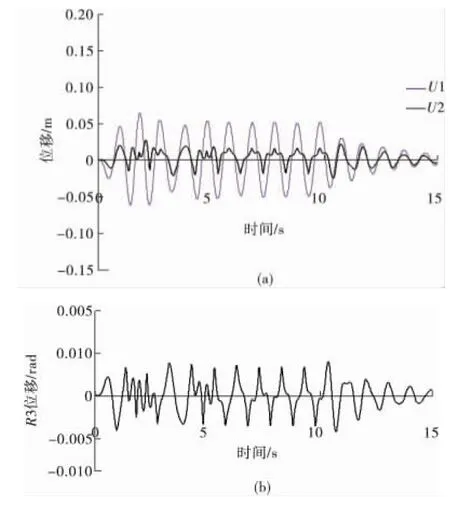
圖7 i端位移Fig.7 Displacement of i-end

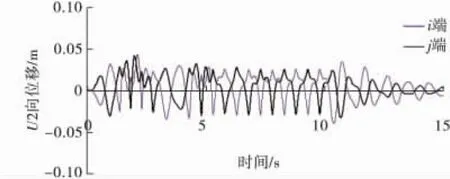
圖8 i端、j端位移Fig.8 Displacement of i-end and j-end

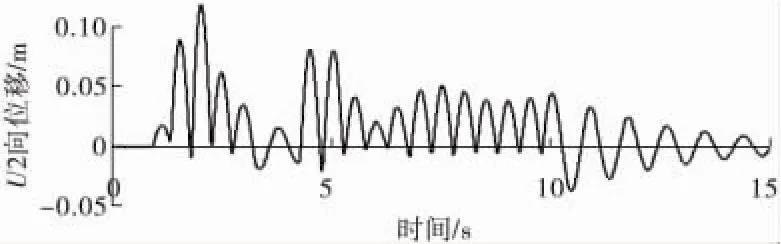
圖9 質心位移Fig.9 Displacement of mass center

通過圖7和圖3的對比可發現，主梁-橋臺相互作用顯著地限制了i端在R3自由度上的位移。由于撞擊力的存在，i端和j端在U2上的位移不再呈對稱關系。事實上，由于主梁-橋臺相互作用方向為梁端切線方向，撞擊力存在橫橋向的分力并導致主梁的橫向位移。圖9顯示了質心位移時程，可看出在撞擊前質心沒有U2向位移;但在第1次撞擊后的整個地震過程中，質心均表現出沿半徑增大方向運動的趨勢。隨著地震作用的結束，質心振動幅值逐漸衰減。

2.3 最不利地震輸入方向的確定

基于本文研究的重點，將導致橋面板發生最大轉動的地震輸入方向定義為最不利地震作用方向。對于非規則橋梁，僅考慮順橋向或橫橋梁的地震作用，其結果偏不安全［7］。目前國內外學者主要通過反應譜法進行地震動雙向輸入計算來考慮地震的空間作用。其中 E.L.Wilson［8］提出了基于反應譜振型疊加法求解最不利地震輸入方向;馮云田，等［9］討論了非規則橋梁的地震輸入主方向對地震反應的影響，認為只需沿結構水平面內任意兩個不重合的方向輸入地震波，就可以確定結構的最不利地震反應;全偉，等［3］則建議用多維地震時程分析來確定地震動輸入的主方向。由于各種方法在確定最不利輸入方向時的標準不同，導致各種方法應用的局限性。我國現行《公路橋梁抗震設計細則》［10］規定:進行曲線橋地震反應分析時，可分別沿相鄰兩橋墩連線方向和垂直于連線水平方向進行多方向地震輸入，以確定最不利地震水平輸入方向。

由于主梁-橋臺相互作用的復雜性，僅按上述方向輸入地震波不能完全計算出橋面板的最大反應，文中通過不斷改變地震輸入角度來確定最不利輸入角度，并從中找出一般規律性。

基于曲率半徑分別為 10，15，20，25，30 m，跨徑為15 m的圓弧線彎橋進行分析，輸入與之前分析相同的地震波。地震輸入方向分別為 0°，10°，20°，30°，40°，50°，60°，70°，80°，90°，其中 0°平行于沿弦線，分別計算考慮碰撞作用和忽略碰撞作用的地震反應。GAP單元參數和方向同之前分析。

圖10為r=10 m時i端地震反應計算結果。對于U2向位移，忽略撞擊作用時，隨著輸入角度的增加，U2方向位移先為逐漸增大，達到峰值后約有減小，最大值為 0.198 m、70°方向輸入;考慮撞擊作用時，U2向最大位移先隨輸入角度的增加而增加，達到峰值后進入相對平穩段。對于R3向位移，忽略撞擊作用時，R3位移隨著輸入角度的增加而減小，最大值為0.132 rad、0°方向輸入;考慮撞擊作用時，R3 位移確呈現先增加、達到峰值后迅速減小的特點。由此可見，考慮撞擊作用時上部結構的R3位移不是導致U2位移的唯一因素，兩者的最大值存在非一致性。

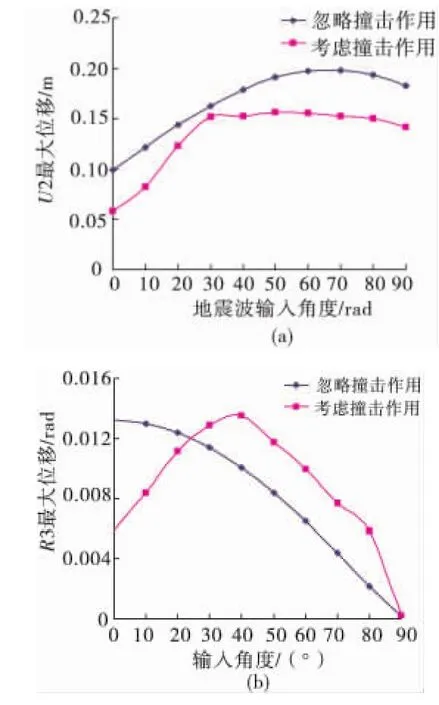
圖10 考慮碰撞作用和忽略碰撞作用的地震反應Fig.10 Seismic response with impact interaction and neglected the interaction

圖11顯示了忽略主梁-橋臺相互作用和考慮該作用作用時不同曲率半徑橋面板最大轉動位移。不考慮主梁橋臺相互作用時，最大轉動隨輸入角度的減小而減小;在相同的地震輸入角度下，曲率半徑大的轉動位移小。考慮該作用時，各個橋臺的轉動隨輸入角度的增加而先增后減;相同的地震輸入角度下，曲率半徑大的轉動也大;且最大轉角均大于忽略主梁-橋臺時的最大轉角。因此，忽略撞擊作用對于橋面板的轉動計算是偏不安全的。

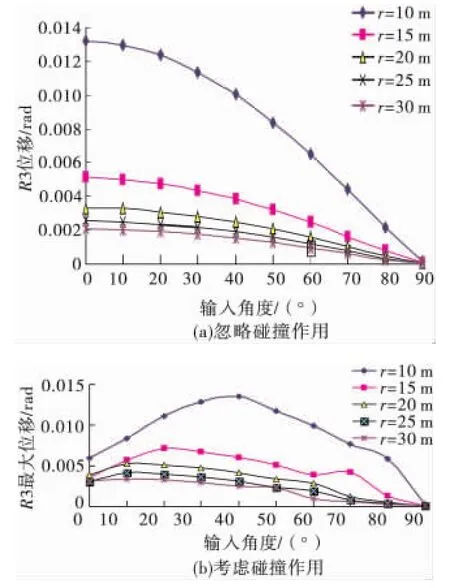
圖11 不同地震輸入方向最大轉角Fig.11 Maximum rotation under different input angle

此外，圖11顯示出最不利輸入角度的趨勢，隨著曲率半徑的增加，最不利輸入角度也隨之增加。計算表明，最不利輸入角度和梁端切線角度有一定關系。

表1顯示了考慮撞擊作用時，各種曲率半徑的曲線梁在切線角度輸入下的最大反應和最不利輸入角度輸入下的最大反應。以α表示最不利輸入角度、β為切線角度。β為45°時，兩者計算差異較大;當β＜30°時，以α向輸入地震波所得到的最大轉角比以β輸入所得反應相差小于3%，因此，在曲線橋梁端切線與弦線夾角較小時，可以弦切線夾角為最不利輸入角度來計算橋面板的最大轉動。

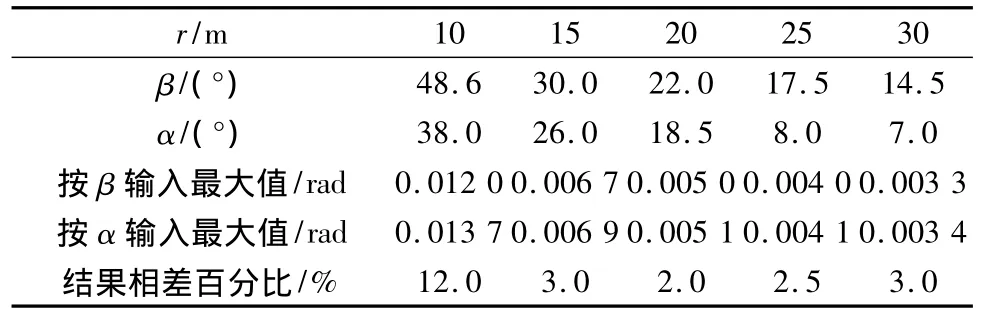
表1 最大轉角計算結果Table 1 Calculation results of maximum totation

3 結語

筆者通過對簡化的單跨曲線橋模型進行動力時程分析，研究了曲線橋在地震作用下的面內轉動機理。該轉動位移同曲線橋自身幾何特征、上部結構約束、地震波輸入方向有直接關系，具體結論如下:

1）彈性支承曲線橋由于自身的幾何特性。在弦線方向的地震輸入下會產生轉動，該位移在梁端表現為兩個主方向的位移耦合。而上部結構質心只存在轉動位移和U 1向的平動位移，未發生U 2向平動位移。對于相同跨徑的曲線橋，曲率半徑越小，轉動越明顯。

2）在沿弦線方向的地震作用下，主梁-橋臺相互作用對曲線橋的轉動有抑制，但質心有向半徑增大方向位移的趨勢。

3）考慮主梁-橋臺相互作用和忽略該作用時，橋面板發生最大轉角所對應的輸入角度不一致，且考慮撞擊作用會得到更大的轉動位移。在既定輸入角度下，橋面板的轉動隨曲率半徑的增大而減小。

4）考慮主梁-橋臺相互作用時，曲線橋的橫向最大位移和面內最大轉角存在非一致性，如何確定導致最大橫向位移的地震作用需要進一步研究。

5）在不同方向的水平地震作用下，忽略撞擊作用時的最不利輸入方向為平行于弦線方向;對于梁端切線和弦線夾角小于30°的曲線橋，可考慮撞擊作用時的最不利輸入方向為平行于切線方向。

（References）:

［1］ Burdette N J，Elnashai A S.Effect of asynchronous earthquake motion on complex bridge 1:Methodology and input motion ［J］.Journal of Bridge Engineering，2008，13（2）:158-165.

［2］ Burdette N J，Elnashai A S.Effect of asynchronous earthquake motion on complex bridge 2:Results and implications on assessment［J］.Journal of Bridge Engineering，2008，13（2）:166-175.

［3］ 全偉，李宏男.曲線橋多維地震時程分析主方向研究［J］.振動與沖擊，2008，27（8）:20-24.

QUAN Wei，LI Hong-nan.Main direction study on curve bridge under multi-dimensional time history analysis during earthquakes［J］.Journal of Vibration and Shock，2008，27（8）:20-24.

［4］ 耿江瑋，朱東生，向中富，等.非規則連續梁橋非線性地震反應分析［J］.重慶交通大學學報:自然科學版，2011，30（2）:185-189.

GENG Jiang-wei，ZHU Dong-sheng，XIANG Zhong-fu，et al.The nonlinear seismic response analysis of irregular continuous bridge［J］.Journal of Chongqing Jiaotong University:Natural Science，2011，30（2）:185-189.

［5］ 李黎，吳璟，葉志雄.隔震曲線橋梁碰撞研究［J］.工程抗震于加固改造，2008，30（5）:48-54.

LI Li，WU Jing，YE Zhi-xiong.Research on pounding of isolated curved bridge［J］.Earthquake Resistant Engineering and Retrofitting，2008，30（5）:48-54.

［6］ 王東升，馮啟民，王國新.基于直桿共軸碰撞理論的橋梁地震反應鄰梁碰撞分析模型［J］.工程力學，2004，21（2）:54-59.

WANG Dong-sheng，FENG Qi-min，WANG Guo-xin.Analysis model of pounding between adjacent bridge girders during earthquakes based on collinear impact between rods［J］.Engineering Mechanics，2004，21（2）:54-59.

［7］ 朱東生，劉世忠，虞廬松.曲線橋地震反應研究［J］.中國公路學報，2002，15（3）:42-48.

ZHU Dong-sheng，LIU Shi-zhong，YU Lu-song.Research on seismic response of curved girder bridges［J］.China Journal of Highway and Transport，2002，15（3）:42-48.

［8］ Wilson E L，Button M R.Three-dimensional dynamic analysis for multi-component earthquake spectra［J］.Earthquake Engineering Structure Dynamics，1982，10（3）:471-476.

［9］ 馮云田，李明瑞.復雜結構的彈性地震反應分析［J］.地震工程與工程振動，1991，11（4）:77-86.

FENG Yun-tian，LI Ming-rui.Elasticity seismic response analysis of complex structure［J］.Earthquake Engineering and Engineering Vibration，1991，11（4）:77-86.

［10］JTG/T B 02-01—2008公路橋梁抗震設計細則［S］.北京:人民交通出版社，2008.

In-Plane Rotation Mechanism of Curve Bridge under Seismic Response

HUANG Ming-fei
（School of Civil Engineering＆ Architecture，Chongqing Jiaotong University，Chongqing 400074，China）

Seismic response of superstructure would appear coupling phenomenon in curve bridge.This phenomenon mainly includes transverse displacement and in-plane rotation.The rotation mechanism of earthquake action in chord direction is researched.Based on the analysis on the simplified single-span curve bridge and linear time-history，the in-plane rotation mechanism of curve bridge is studied，and different seismic responses with different curvature ratio are compared.The effect of the girder-abutment interaction on the in-plane rotation is discussed.Nonlinear time-history method is applied to calculate the seismic response with different curvature and different input direction.Finally，the most adverse input angle of earthquake is determined.

curve bridge;seismic response;in-plane rotation;earthquake input angle

U441.3

A

1674-0696（2011）06-1265-05

10.3969/j.issn.1674-0696.2011.06.01

2010-06-17;

2011-07-17

黃明非（1987-），男，重慶人，碩士研究生，主要從事橋梁抗震方面的研究。E-mail:huangmingff@163.com。