計算機原理之進制篇——如何學好進制初探

上海電子工業學校 上海信息職業技術學院 余 浩

在講如何學好進制之前，我們先來看以下三個二進制數，算一算它們所對應的十進制數是多少。

①1O11 ②1111111O11 ③1O111O11

如果你能花1分鐘做出來，說明你已經學會進制轉換了，請跳過本文的第一部分，直接閱讀第二部分；如果你能在1分鐘以內完成（本人大概需要花十秒左右可以解出答案），那說明你已經是一個進制轉換的高手了，可快速瀏覽本文，當然不看也沒有問題；如果你花了幾分鐘才計算出來，或者說無法確定答案是否正確的話，那你就得加油了，請認真仔細地并反復地閱讀本文，相信會有大收獲。

一、進制基礎

大家都知道：二進制是計算機內部數據處理和數字電路的基礎。進制掌握得是否清楚，對后續很多相關課程的學習影響重大。很多人在學習進制的時候覺得猶如在“看天書”，或者是似懂非懂，一知半解，究其原因是平時用慣了十進制，看見“1O”就是“十”。而當你學過進制后，“1O”有可能是“二”，也有可能是“八”；或者是“十六”，結果取決于采用的是幾進制數。

學好進制，首先要學好二進制，學好二進制的基礎有兩點：

1.熟練掌握二進制數運算中最復雜的計算，即1+1=(1O)2（逢二進一，類似于十進制中的9+1）；再推出(11)2+1=(1OO)2……

2.熟記2的N次方的數（即二進制的權，權的大小與數字符號所在位置有關）；2O=1，21=2，22=4，23=8，24=16，25=32，26=64，27=128，28=256，29=512。

一般記到2的1O次方，2的11次方可以用2K來表示，即1K=1O24=21O，22O=1M=1O24K，23O=1G=1O24M，24O=1T=1O24G，264=24·22O·24O=16MT。

運用以上兩點，從O開始依次加1，可推出四位二進制數，并計算其所對應的十進制數。

接下來，我們來看看4位二進制部與其它進制的對應關系表（見表1）。

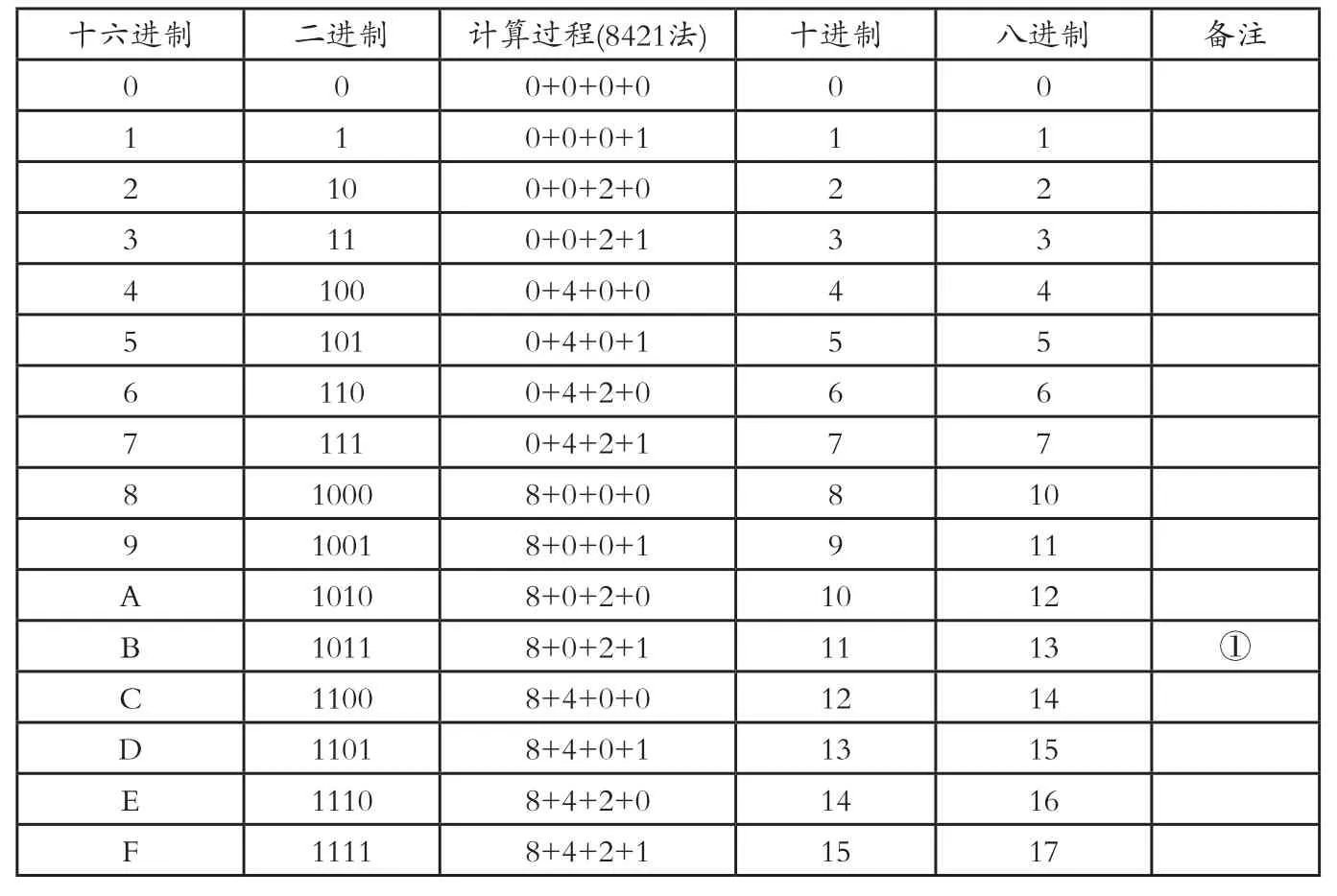
表1 4位二進制數與其它進制對應表

·任何進制數轉換成十進制數都可以用按權展開求和的方法。

8、4、2、1都是二進制的權，8421法其實就是四位數的按權展開求和法。（注意不要與8421碼概念混淆，8421碼是一種BCD編碼，用四位二進制編碼來表示十進制的十個值。·十進制轉換成其它進制數，都可以用除以基數，倒過來取余數的方法。

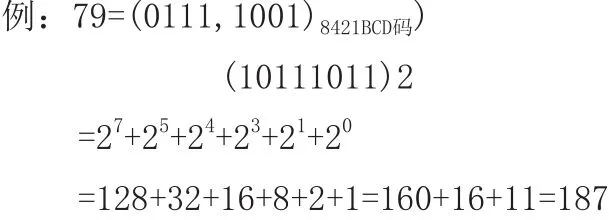
基數即為該進制能采用的基本符號，而余數肯定都是小于基數的。

例如：二進制的基數為2，只有“O”和“1”兩個基本符號。十進制數除以二，得到的余數也只會是“O”或者“1”。而十六進制較復雜，用“A”表示1O，依次類推，逢十六進位。

·2位二進制數最大為“11”，八進制數為“77”；十進制數為“99”；而十六進制數則為“FF”。

·十六進制數、八進制數可直接轉換成二進制數。

16是2的4次方；8是2的3次方。因此，八進制數和十六進制數與二進制數的關系緊密（通俗地講可以看成是親戚關系——看到二進制，馬上就知道八進制和十六進制數長什么樣）。

只要充分理解和熟記牢記表1，那你離成為進制高手就不遠了。

二、進制提高

現在讓我們來看看如何在很短的時間內計算出這三個二進制數所對應的十進制數。

①1O11

當然直接從基本的四位二進制數與十進制數的對應表中取出答案：為“十一”。（牢記在腦中，最差也要知道“8+2+1”）

②1111111O11

可看成1111111111減去1OO所得。1O位二進制“1”等于2的1O次方減1，即1O24－1=1O23。而二進制“1OO”為十進制的“四”。故最后答案為1O23－4=1O19。

另外的一個算法可以先算出前7個“1”的十進制數等于2的7次方減1，即128－1=127，然后乘以二進制數“1OOO”，即十進制數“8”；最后加上3，得到最后結果為：127*8+3=125*8+2*8+3=1OOO+19=1O 19。對應的二進制數算式為：1111111*1O OO+11=1111111OOO+11=1111111O11。

③1O111O11

先把該數看成十六進制為：BBH，再轉換成十進制數（十六進制“B”等于十進制數“11”），即為11*16+11=176+11=187。

·從以上三道小題計算過程來看，首先，再次驗證了進制的基礎

（1）要牢牢記住四位二進制數對應的十進制數和十六進制數；

（2）要牢牢記住2的O次方到2的1O次方所對應的十進制數。

·然后我們再來看一些特殊二進制數的計算，見表2

（1）“1”后面有N個零的二進制數等于2的N次方（這和十進制“1OO”即1O的平方的道理是一樣的）；

例：2、4、8、16、32所對應的二進制數。

（2）N個全“1”的二進制數等于2N-1（這和十進制數“99”等于“1OO－1”的道理是一樣的）。

例：127=27－1=(1111111)2

·接著，我們來看二進制的乘法可以用移位添O來代替

因為二進制乘法很簡單，沒有乘法口訣表需要去背，要么乘“O”，得全“O”；要么乘“1”，得其本身。

二進制數向左移位，末位添O，即乘2（二進制數“1O”）。若添2個O，即乘4（二進制數“1OO”）；添3個O，即乘8（二進制數“1OOO”）；依次類推，添N個O，即乘2的N次方。

例：(1O1OOO)2=(1O1*1OOO)2=5*8=4O；(11111OO)2=(11111*1OO)2=31*4=124。

·最后，我們對以上所述進行一下總結和綜合：

1.二進制數中“1”的個數不多，仍可用按權展開求和法。

例：(1O1O1OO)2=26+24+22=64+16+4=84(=5*16+4=1O*8+4)

2.二進制數中“1”的個數較多，可運用計算全“1”的方法再通過加減獲得。

例：(1111O111)2=(11111111－1OOO)2=255－8=247

或：=(1111*1OOOO+111)2=15*16+7=2 56-16+7=247

表2 特殊的二進制數

二進制 十進制 十六進制 八進制 備注10,000 16 10 20 11,111 31 1F 37 100,000 32 20 40 111,111 63 3F 77 1,000,000 64 40 100 1,111,111 127 7F 177 10,000,000 128 80 200 11,111,111 255 FF 377 100,000,000 256 100 400 111,111,111 511 1FF 777 1,000,000,000 512 200 1000 1,111,111,111 1023 3FF 1777 10,000,000,000 1024 400 2000

3.一定要活用移位（即乘除法），并牢記四位二進制數對應的十六（八）進制數值。見例1、2下劃線對應加粗部分的運算過程。

例：(2FC)16=(1O111111OO)2=29+28-1-3=512+256-4=764

4.八進制介于二進制與十六進制之間，因此可以用于過渡計算。如：將較大的十進制數轉換成二進制數時，可以先計算成八進制數（除8比除16簡單），再通過1位對3位來快速獲得二進制數（當然以熟悉表1為前提）。

例：115=(163)8=(1,11O,O11)2

115=14*8+3=(1*8+6)*8+3(遞推式，在編程時會用到)

5.如果熟悉了進制，那么很多進制轉換都可以很快計算出來。

例：（1）將十進制數“252”轉換成八進制數（不需要用除8取余法）

252=255-3=(11111111-11)2=(11 111 1OO)2=(374)8

（2）將十進制數“24O”轉換成八進制數（不需要用除8取余法)

32O=5*8*8=(1O1*1O*1O)8=(1O1OO)8

以上這些運算，都必須在熟悉常用進制的權，以及4位二進制數對應八、十六進制數的前提下，才能迅速準確地完成。

只有真正理解了二進制(包括運算和特性)，其它進制就能迎刃而解了。

計算有很多技巧。如果讓你計算“99×99=？”，有經驗的你一定會這么算：(1OO-1)×99=99OO-99=98O1（其實還有其它技巧可以很快心算出來，在電視節目中有過介紹）。同理，若要將1O位以內的二進制數轉換成十進制數，可運用以上方法很快心算出來，但若二進制數超過1O位以上，除非“1”的個數不多，否則還是要花一定的時間進行計算，甚至要動用計算工具。當然或許有人不用就能辦到，這就是“世界之大，無奇不有啊”。

謹以此文獻給那些學習進制比較困難的朋友，希望能對大家學習進制有所幫助和提高。通過對此文的閱讀理解，利用閑暇時間的反復訓練和再學習，我相信每個人都可以牢牢地“Hold”住它，成為真正的“進制控”。

注：文中除有文字描述的或有下標標注的數字外（也有用符號表示的，十六進制——H；十進制——D；八進制——Q；二進制——B，由于容易和十六進制的基本符號產生混淆，故本文中未采用），其它出現的阿拉伯數字都為十進制數。

再做幾道進制轉換的題目，看看有沒有進步：

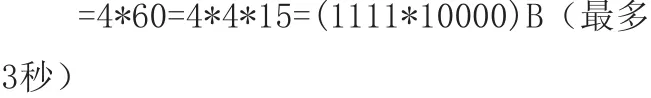
[1]侯炳輝.計算機原理[M].經濟科學出版社.

[2]電子技術基礎·數字部分(第四版)[M].高等教育出版社.