基于最大不失磁電流的表貼式永磁電機(jī)性能分析*
畢劉新, 王善銘, 楊平西
(1.中船重工集團(tuán)公司第704研究所,上海 200031;2.清華大學(xué)電機(jī)工程與應(yīng)用電子技術(shù)系,北京 100084)
0 引言
釹鐵硼的應(yīng)用使永磁電機(jī)的功率密度和效率都有了很大提高,表貼式永磁電機(jī)卓越的控制性能使其在變速驅(qū)動(dòng)系統(tǒng)中得到了廣泛應(yīng)用,但是永磁體的潛在失磁危險(xiǎn)一直制約著其在高可靠領(lǐng)域的應(yīng)用[1-2]。高溫、劇烈震動(dòng)及沖擊電流產(chǎn)生的電樞反應(yīng)均可造成永磁材料的不可逆去磁,使電機(jī)性能降低甚至無(wú)法使用[1]。本文僅關(guān)注于電樞反應(yīng)產(chǎn)生的去磁效應(yīng),通過建立最大不失磁電流與永磁電機(jī)結(jié)構(gòu)尺寸之間的關(guān)系,推導(dǎo)出電機(jī)的運(yùn)行極限,為永磁電機(jī)的設(shè)計(jì)以及變頻器供電情況下的安全運(yùn)行提供依據(jù)。
文獻(xiàn)[3]分析了永磁材料在快速交變磁場(chǎng)作用下的磁化和退磁規(guī)律,并在此基礎(chǔ)上初步探討了永磁材料的交流失磁機(jī)理。文獻(xiàn)[1-4]分別用磁路法和有限元法對(duì)永磁電機(jī)的失磁特性進(jìn)行了研究,但均不夠簡(jiǎn)單直觀。文獻(xiàn)[6-9]研究了電樞電流對(duì)永磁電機(jī)的去磁特性,但沒有據(jù)此對(duì)電機(jī)的性能進(jìn)行更深入的研究,也未推廣至多相電機(jī)。
本文根據(jù)永磁體的退磁特性,推導(dǎo)了表貼式永磁電機(jī)的最大不失磁電流解析計(jì)算公式,分析了電機(jī)的相關(guān)性能與提高的措施,且本文公式均可用于多相永磁電機(jī),最后通過有限元仿真,驗(yàn)證了最大不失磁電流解析計(jì)算公式的正確性。
1 最大不失磁電流
1.1 永磁電機(jī)的結(jié)構(gòu)描述
圖1為表貼式永磁電機(jī)的結(jié)構(gòu)示意圖,齒槽效應(yīng)通過卡氏系數(shù)計(jì)入,圖中的氣隙長(zhǎng)度為有效氣隙長(zhǎng)度。
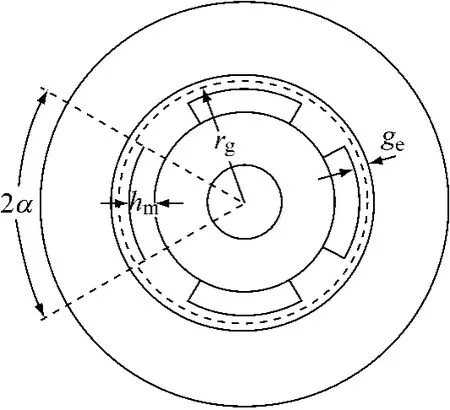
圖1 表貼式永磁電機(jī)橫截面示意圖
圖中:ge——有效氣隙長(zhǎng)度;
hm——永磁體厚度;
rg——?dú)庀栋霃?
2α——每極下永磁體覆蓋的電角度。
1.2 釹鐵硼永磁材料的退磁曲線
典型的釹鐵硼永磁材料的退磁曲線如圖2所示,D點(diǎn)稱之為拐點(diǎn),D點(diǎn)以上部分的回復(fù)線同退磁曲線重合為一直線,永磁電機(jī)的磁性能在該區(qū)間保持穩(wěn)定,一旦退磁磁場(chǎng)強(qiáng)度超過Hd后,退磁曲線急劇下降,此時(shí)回復(fù)線與退磁曲線不再重合,造成永磁體的不可逆去磁,進(jìn)而導(dǎo)致電機(jī)的性能變差。因此,永磁電機(jī)在運(yùn)行中必須保證永磁體的退磁磁場(chǎng)強(qiáng)度不得超過Hd。
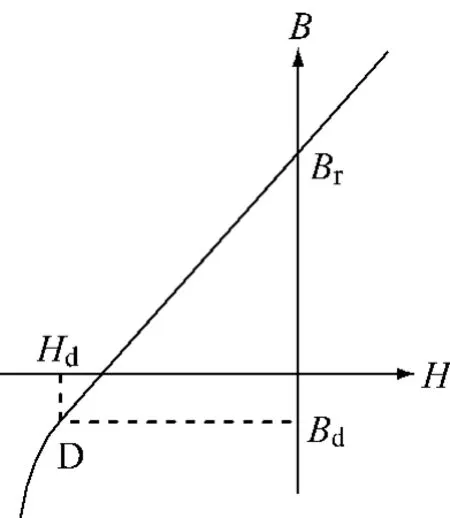
圖2 釹鐵硼永磁材料的退磁曲線
圖中:Br——永磁體的剩磁密度;
Bd——失磁點(diǎn)對(duì)應(yīng)的磁密。
1.3 最大不失磁電流推導(dǎo)
圖3所示為永磁磁極和定子電樞電流共同產(chǎn)生氣隙磁密的過程,忽略鐵心飽和,其中β是定子磁動(dòng)勢(shì)軸線超前轉(zhuǎn)子d軸的電角度,稱之為內(nèi)功率因數(shù)角。
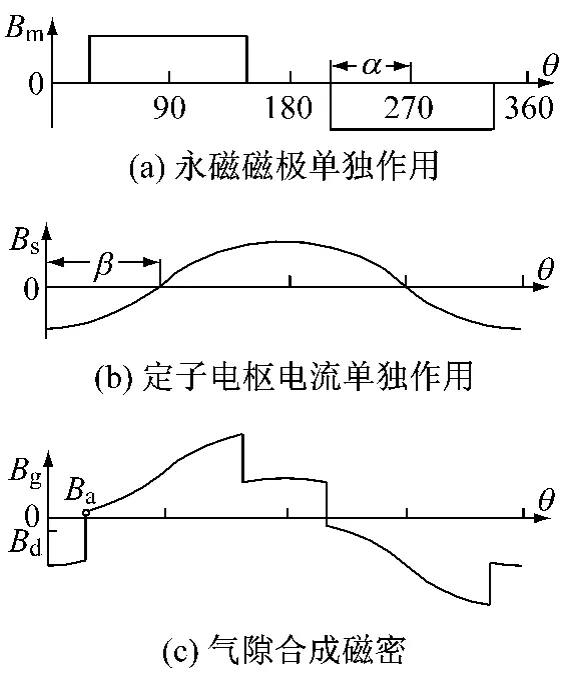
圖3 氣隙合成磁密示意圖
圖3(a)為永磁磁極單獨(dú)作用時(shí)產(chǎn)生的磁密分布示意圖,其中:
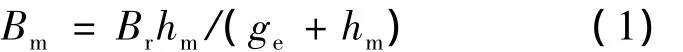
圖3(b)為定子電樞電流單獨(dú)作用時(shí)產(chǎn)生的空間基波磁密波形示意圖,其磁密幅值為
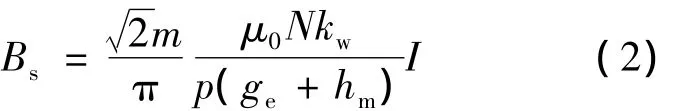
式中:m——電機(jī)相數(shù);
N——每相繞組串聯(lián)匝數(shù);
kw——基波繞組因數(shù);
p——極對(duì)數(shù);
I——相電流有效值。
圖3(c)為氣隙合成磁密示意圖,當(dāng)采用Id=0的控制方法時(shí),β=90°,對(duì)應(yīng)的電樞電流為交軸性質(zhì)的,此時(shí)在圖中的黑點(diǎn)標(biāo)注處永磁體承受最大的退磁磁場(chǎng)強(qiáng)度,為避免不可逆去磁,必須保證Ba>Bd[8],即
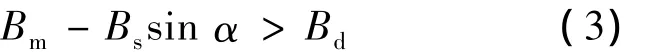
將式(1)、(2)代入式(3)可得到交軸性質(zhì)的最大相電流有效值:
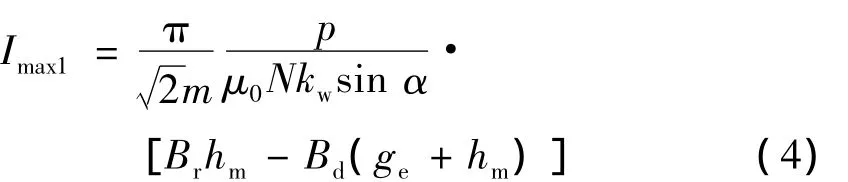
當(dāng)β=180°時(shí),電樞電流為去磁性質(zhì)的直軸電流,此時(shí)的定子相電流最大值為
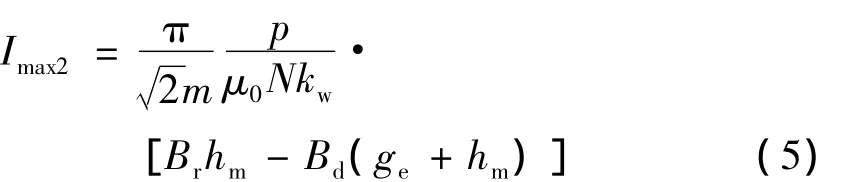
由式(4)、(5)可得出以下結(jié)論:
(1)交軸電流對(duì)永磁體的退磁效應(yīng)小于去磁性質(zhì)的直軸電流;
(2)增加極對(duì)數(shù)時(shí),每極下的電樞磁動(dòng)勢(shì)減小,電樞反應(yīng)對(duì)永磁體的去磁效應(yīng)減弱;
(3)增大永磁體厚度和采用高剩磁密的永磁體可提高最大不失磁電流。
2 永磁電機(jī)性能分析
以最大不失磁電流為基礎(chǔ),可以進(jìn)行永磁電機(jī)的性能分析。
2.1 最大轉(zhuǎn)矩能力
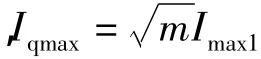
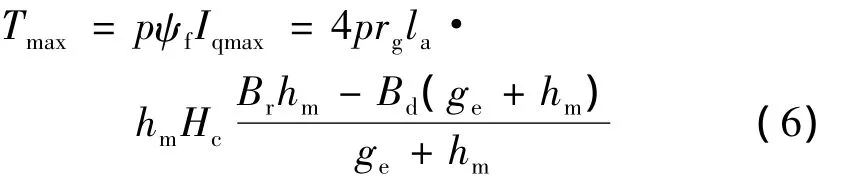
式中:la——電樞鐵心長(zhǎng)度;
Hc——永磁體矯頑力。
假設(shè)Bd=0,則式(6)簡(jiǎn)化為
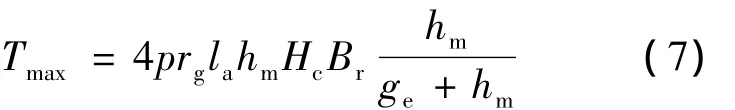
由式(7)可得出如下結(jié)論:
(1)最大轉(zhuǎn)矩與電機(jī)相數(shù)無(wú)關(guān);
(2)最大轉(zhuǎn)矩與極對(duì)數(shù)、氣隙半徑及電樞長(zhǎng)度成正比;
(3)增大永磁體厚度和采用高磁能積HcBr的永磁體可提高最大轉(zhuǎn)矩。
2.2 最大氣隙剪切力密度
氣隙剪切力為電樞單位表面積的平均電磁切應(yīng)力,由定義可知:最大轉(zhuǎn)矩對(duì)應(yīng)的氣隙剪切力密度為
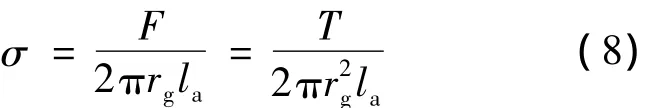
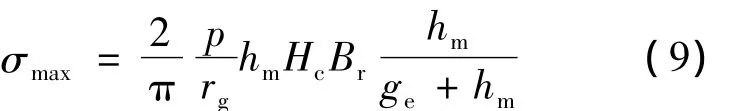
氣隙剪切力密度是電機(jī)的一個(gè)非常重要的指標(biāo),表征著單位電機(jī)轉(zhuǎn)子體積產(chǎn)生的轉(zhuǎn)矩,反映了電機(jī)材料利用率,為提高氣隙剪切力密度可采取以下措施:
(1)提高永磁體的最大磁能積;
(2)增加永磁體厚度,盡可能減小氣隙長(zhǎng)度;
(3)增加極對(duì)數(shù),減小轉(zhuǎn)子半徑,但是電機(jī)設(shè)計(jì)中,很難兼顧這兩點(diǎn),一般當(dāng)極對(duì)數(shù)增加時(shí)要相應(yīng)增加電機(jī)的半徑。
2.3 最大加速能力
徑向電機(jī)的轉(zhuǎn)子可以看作一個(gè)圓柱體,其轉(zhuǎn)動(dòng)慣量約為

式中:ρ——轉(zhuǎn)子材料密度。
結(jié)合式(7)、(10)可以得到永磁電機(jī)的最大加速性能:
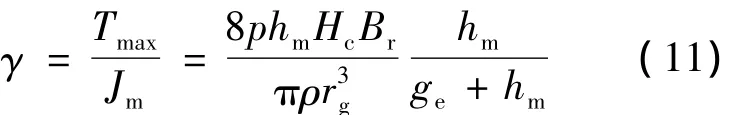
在需要快速響應(yīng)的場(chǎng)合,往往要求電機(jī)具有盡可能大的加速性能,根據(jù)式(11)可采取以下措施來提高:
(1)減小轉(zhuǎn)子半徑;
(2)增加極對(duì)數(shù);
(3)增大永磁體厚度和采用高磁能積的永磁體。
3 有限元驗(yàn)證
由于電機(jī)的性能分析是基于最大不失磁電流進(jìn)行的,因此本文僅對(duì)最大不失磁電流進(jìn)行驗(yàn)證。基本思路是:當(dāng)電樞繞組通最大不失磁電流時(shí),查看永磁磁極范圍內(nèi)的氣隙合成磁密是否等于永磁體失磁點(diǎn)對(duì)應(yīng)的磁密Bd,以此驗(yàn)證最大不失磁電流解析計(jì)算公式的正確性。
3.1 仿真用電機(jī)數(shù)據(jù)
本文采用的多相永磁電機(jī)的主要參數(shù)如表1所示,其中鐵心材料采用DW315,具體磁化曲線參見文獻(xiàn)[1]后的附錄。
根據(jù)前文的解析公式計(jì)算結(jié)果如表2所示。
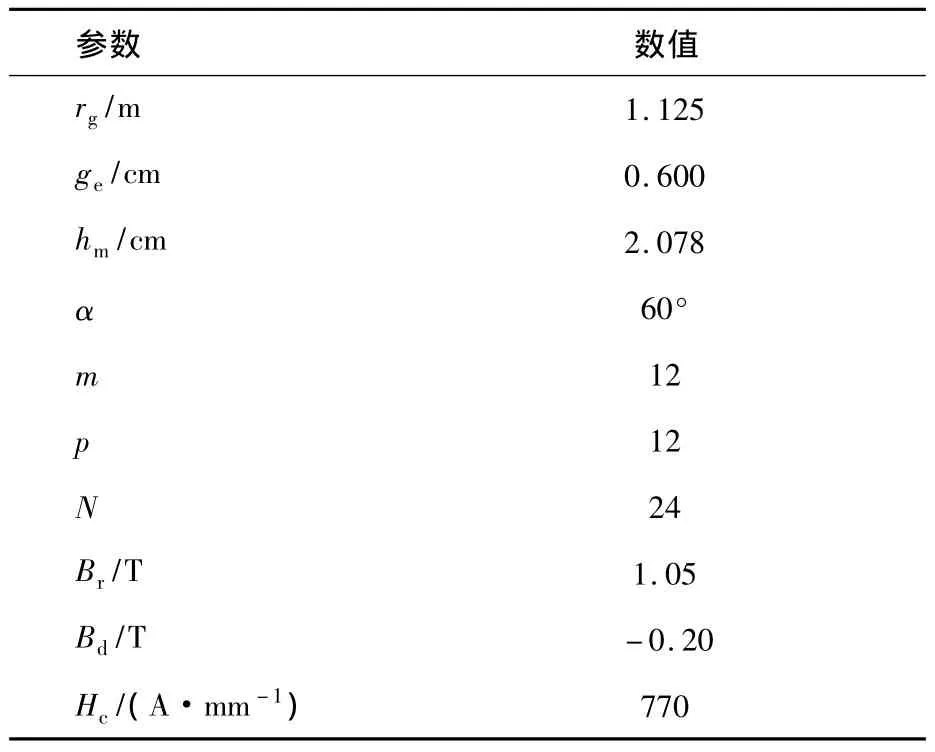
表1 主要尺寸和參數(shù)
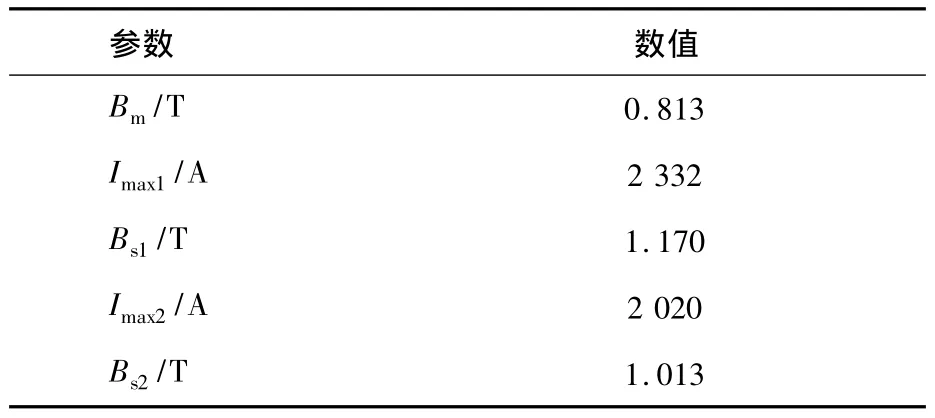
表2 解析計(jì)算結(jié)果
3.2 有限元仿真結(jié)果
本文采用ANSYS仿真軟件對(duì)電機(jī)進(jìn)行二維的靜磁場(chǎng)分析。圖4為永磁電機(jī)一對(duì)極下的有限元模型與網(wǎng)格剖分。其中邊界條件設(shè)置情況如下:定子外邊界和轉(zhuǎn)子內(nèi)邊界磁矢位均設(shè)置為0;兩側(cè)設(shè)置為偶對(duì)稱周期性邊界條件。由于氣隙相對(duì)很小,可以取氣隙中間的徑向磁密代替永磁磁極外邊緣的磁密。
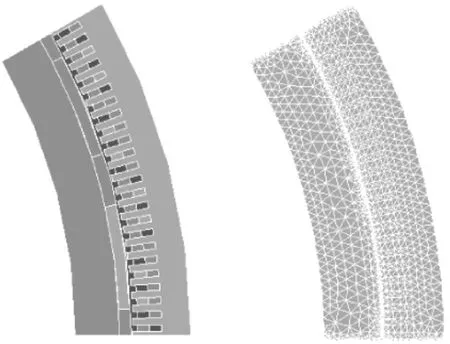
圖4 有限元模型與網(wǎng)格剖分
圖5(a)為永磁體單獨(dú)作用時(shí)的氣隙磁密波形,磁極范圍內(nèi)的磁密平均值與解析解0.813 T非常接近。
圖5(b)、(d)分別為 Imax1=2 332 A,β =90°和Imax2=2 020 A,β=180°時(shí),電樞電流單獨(dú)作用下的徑向氣隙磁密波形。由于鐵心飽和的原因,其基波幅值較解析解稍小。
圖5(c)為Imax1=2 332 A,β=90°時(shí)的氣隙合成磁密波形,其中虛線為(a)、(b)波形直接疊加的結(jié)果,實(shí)線為實(shí)際的合成磁密波形,兩者比較可以清晰地看出鐵心飽和的影響。實(shí)線的加粗部分對(duì)應(yīng)于 60°~120°的磁極范圍,其最小值約為0 T,與解析計(jì)算結(jié)果的-0.2 T有些出入,原因主要在于解析解僅考慮了電樞磁動(dòng)勢(shì)的基波效應(yīng),且忽略了飽和效應(yīng)。
圖5(e)為 Imax2=2 020 A,β =180°時(shí)的氣隙合成磁密波形,在直軸去磁性電樞電流的作用下,合成氣隙磁密幅值較小,鐵心未飽和,因此電樞電流實(shí)際的去磁效應(yīng)比考慮了飽和效應(yīng)的圖5(d)中的要大,更加接近忽略飽和的解析計(jì)算結(jié)果。但是由于齒槽效應(yīng)帶來的磁導(dǎo)不均勻,在60°~120°磁極范圍內(nèi),最小磁密值為-0.4T,較理論值-0.2 T稍小,因此在實(shí)際應(yīng)用中,最大不失磁電流的確定需要考慮相應(yīng)的安全系數(shù)。
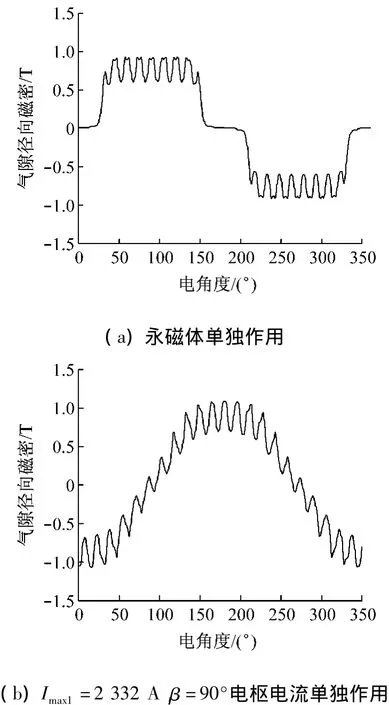
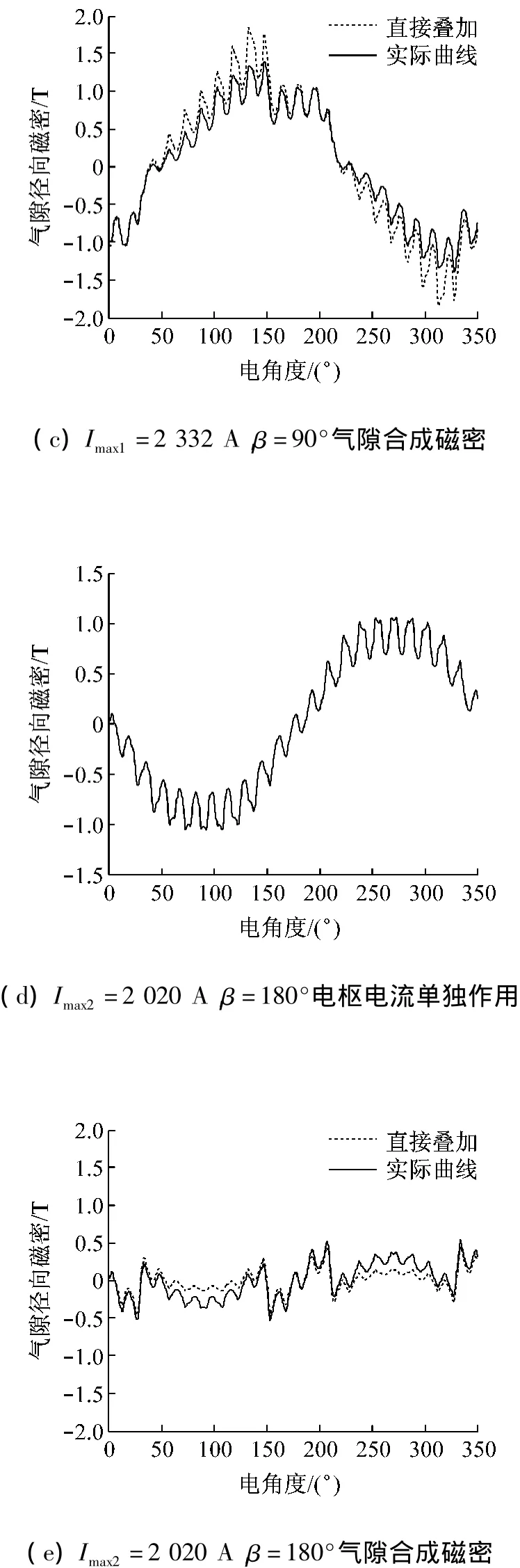
圖5 有限元仿真波形
4 結(jié) 語(yǔ)
本文在僅考慮電樞電流基波磁動(dòng)勢(shì)與忽略鐵心飽和的情況下,根據(jù)永磁體的退磁特性推導(dǎo)出了永磁電機(jī)交軸和直軸性質(zhì)的最大不失磁電流解析表達(dá)式,并以此為依據(jù)分析了永磁電機(jī)的有關(guān)性能,總結(jié)了相應(yīng)的提高措施。這些解析公式將電機(jī)的尺寸結(jié)構(gòu)與性能聯(lián)系起來,為永磁電機(jī)的設(shè)計(jì)和優(yōu)化,以及變頻器供電時(shí)運(yùn)行極限的確定提供了依據(jù)。本文中的公式同樣適用于多相永磁電機(jī)。有限元仿真波形與解析計(jì)算結(jié)果很好地吻合,證明了本文提出的解析公式的正確性。
[1]唐任遠(yuǎn).現(xiàn)代永磁電機(jī)理論與設(shè)計(jì)[M].北京:機(jī)械工業(yè)出版社,1997.
[2]王秀和.永磁電機(jī)[M].北京:中國(guó)電力出版社,2007.
[3]黃浩,柴建云,姜忠良,等.釹鐵硼稀土永磁材料交流失磁[J].清華大學(xué)學(xué)報(bào),2004,44(6):721-724.
[4]何山,王維慶,吳小艷,等.永磁同步發(fā)電機(jī)電樞反應(yīng)去磁效應(yīng)的分析[J].防爆電機(jī),2005,40(2):8-10.
[5]畢劉新.表貼式多相永磁電機(jī)的設(shè)計(jì)與優(yōu)化[D].北京:清華大學(xué),2009.
[6]Sebastian T,Slemon G R.Transient modeling and performance of variable-speed permanent-magnet motors[J].IEEE Transactions on Industry Applications,1989,25(1):101-106.
[7]Sebastian T,Slemon G R.Operating limits of inverterdriven permanent magnet motor drives[J].IEEE Transactions on Industry Applications,1987,23(2):327-333.
[8]Sebastian T,Slemon G R.Transient torque and short circuit capabilities of variable speed permanent magnet motors[J].IEEE Transactions on Magnetics,1987,23(5):3619-3621.
[9]Slemon G R.On the design of high-performance surface-mounted PM motors[J].IEEE Transactions on Industry Applications,1994,30(1):134-140.

