基于火力協同的攻擊機對地突擊研究*
陳 榕 嚴建鋼
(海軍航空工程學院 煙臺 264001)
1 引言
《俄軍合同戰斗原則》明確指出:“沒有協同便沒有勝利”[1]。《美軍作戰手冊》指出:美國海軍作戰要則重要的一條就是“協調配合,相互支援,形成整體作戰力量”[2]。由此可見,協同作戰的重要性。協同是各種作戰力量按照統一的協同計劃在行動上協調配合[3]。由于受掛載方案的限制,飛機遂行對地攻擊任務時,單機能夠掛載的空地武器數量有限且不能同時掛載部分異型空地武器。為了充分發揮突擊作戰各階段不同空地武器的優勢,取得最大的突擊效果,飛機之間的協同作戰十分必要[4]。
為提高攻擊機對地突擊效能,展開基于火力協同的對地突擊研究十分必要。
2 攻擊機協同對地突擊
2.1 攻擊機對地突擊的火力協同
攻擊機編隊對地突擊過程中,可以把其視為一個復合系統,各階段突擊過程看作它的子系統,且具有自組織的特點。該體系良好運行,各子系統相互協調的工作,才能充分發揮整個突擊編隊的作用,最大限度的打擊敵地面目標。子系統之間的這種相互協調使用的程度稱為協同度[5]。
一個協同的復合系統具有整體性、轉換性和自組織性等基本性質[6],而攻擊機編隊對地突擊的火力協同同樣具有以上三種性質。整體性表現在各突擊飛機的目的皆為打擊敵方地面目標,因此各突擊飛機之間有著內部的連續性和整體性。對地突擊的連續性則表現在空地對抗的動態過程中。出于對抗的動態性,使得突擊的不同階段之間存在著轉換的可能,比如遠程導彈攻擊轉為臨空轟炸等。自組織是不同階段突擊手段之間存在著協同配合的特性,在敵方地面目標等外界因素的影響下,從一種無序狀態向有序狀態轉化,構成了系統的自組織性,最后實現了航空兵對地突擊的火力協同。
2.2 攻擊機協同對地突擊模型
根據編隊機載對地武器的射程可分為不同的階段。在某些階段,只能使用某種武器進行攻擊;而在另外某些階段,可供選擇的突擊武器有多種[7]。
攻擊機協同對地突擊的目標是在攻擊過程的不同階段,選擇最優的火力協同方案,獲得最大的全程作戰效能。攻擊機協同突擊地面目標群作戰的數學模型如下:
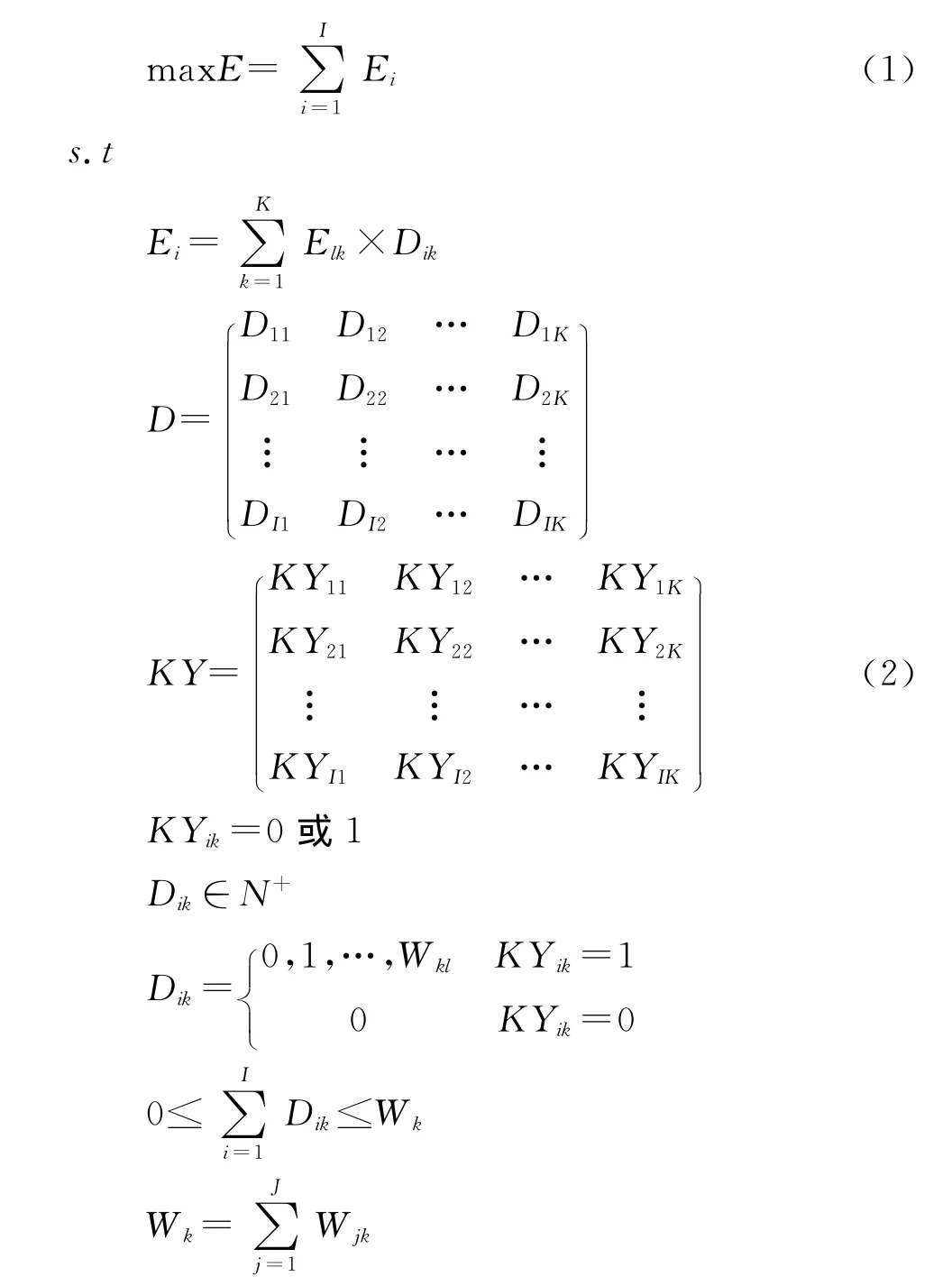
式中,E為全程作戰效能,Ei為第i階段作戰效能,i=1,2,…,I為作戰階段,Elk(l,k=1,2,…,K)為武器間的協同效能。Dik為決策矩陣,表示第i階段發射第k種武器數量。KY為可用武器約束矩陣,KYik表示第i階段第k種武器是否可用,0表示不可用,1表示可用。Wjk為第j架飛機掛載第k種武器數量,Wkl為第k種武器齊射數量的上限。J為編隊飛機架數。
2.3 基于可攻擊區的協同度
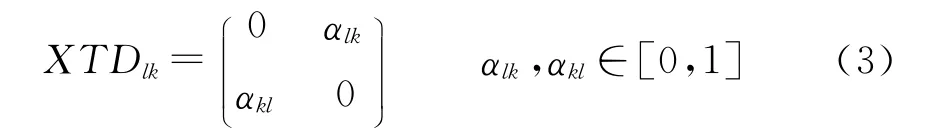
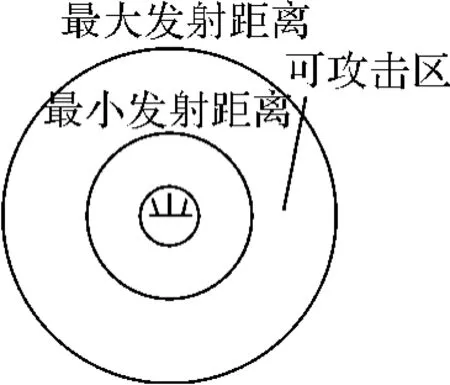
圖1 可攻擊區示意圖
機載對地武器的最大發射距離線和最小發射距離線在地面上的投影稱為該空地武器的可攻擊區,如圖1所示。其中,最大發射距離線是確保空地武器能夠打擊敵方地面目標的開始線,即敵目標離最大發射距離線的距離不大于空地武器的最大射程;最小發射距離線是確保空地武器能夠打擊敵方地面目標的終止線,即敵目標離最小發射距離線的距離不小于空地武器的最小射程。
火力突擊機會窗口,是指載機進入火力可攻擊區時刻起,至離開火力可攻擊區時刻止的時間。在航空兵對地突擊作戰過程中,該空地武器必須在這段時間內發射,否則載機將離開火力可攻擊區,從而錯失發射該空地武器攻擊敵目標的機會[8]。
對于空地武器來說,設第l型空地武器對目標m的機會窗口為tlm,則載機必須在tlm這段時間內發射該武器攻擊敵目標,否則該空地武器不能用于攻擊該目標,若要遂行攻擊,需選擇其它可用的空地武器。
對于機載空地武器的可攻擊區來說,編隊內不同載機掛載空地武器的火力突擊機會窗口在橫向上有重疊或橫向和縱向上都有重疊,在火力突擊時必須進行協調配合。其協調方法,可用可攻擊區協同度來表示。
設有空地武器l和空地武器k。l型空地武器對目標m的機會窗口為tlm,k型空地武器對目標m的機會窗口為tkm,載機在協作域內的逗留時間為Δtm。令αlk為空地武器l與k的協同系數,則空地武器l與k的協同度矩陣為[9]
1)如果αilk=0,(l≠k),表示空地武器l與k無協作關系,它們各自可攻擊區是孤立的;如果任意αlk=0,(l≠k),則編隊內空地武器不存在協作環,協作域為空,即所有空地武器都將獨立射擊,沒有協作關系。
2)如果αlk=1,(l≠k),則表示空地武器l與k有協作關系,且選擇任一武器攻擊都具有相同的時間效應。
3)如果0<αlk<1,(l≠k),則表示空地武器l與k有協作關系,且選擇不同的武器攻擊具有不同的時間效應。如果αlk>αkl說明空地武器l對該目標的射擊時間要小于空地武器k對該目標的射擊時間。
由以上分析可得K種空地武器對地攻擊的協同度矩陣為:
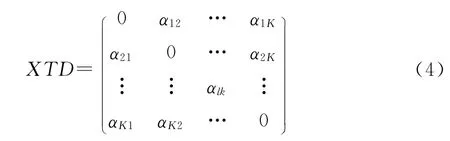
式中αlk(l≠k,l,k=1,2,…,K)定義與式(3)中相同。
3 攻擊機協同對地突擊效能
空中編隊對地突擊過程可以簡化為幾個區間,所以用區間表示編隊對地突擊過程的發展。由于各階段火力協同度的不同每個區間的突擊效能也有所不同。構造兩個集合,一個集合是方案集,為{Al},l=1,2,…,K,另外一個集合是作戰階段集,用{Bi},i=1,2,…,I來表示。首先確定子方案的基礎效能EJlk及其協同度。然后再確定此時刻在考慮協同情況下的該子方案作戰效能為[10]
Elk=EJlk(1+XTDlk) (5)
式中,EJlk為作戰方案Al在作戰區域Bi中的基本作戰效能。XTDlk表示在Bi作戰階段中,作戰方案Al與其它n-1種方案的協同度。
由此可以生成不同武器間協同的作戰效能矩陣,即:

針對2.2節的突擊模型,可運用動態規劃的方法求解最優突擊方案。
4 基于可攻擊區協同度的飛機突擊方案實例分析
作戰想定:紅方4架攻擊組成的編隊對藍方某地面目標群實施突擊。分別掛載編號為1、2、3、4的空地武器,其射程、對目標的作戰效能及掛載數量如表1所示。由于導引頭之間的干擾,除武器4外,武器1、2、3每階段最多只能齊射2枚。
根據4種武器的射程,突擊過程可分為4個階段,即180~100km階段;100~60km階段;60~15km階段;15~10km階段。
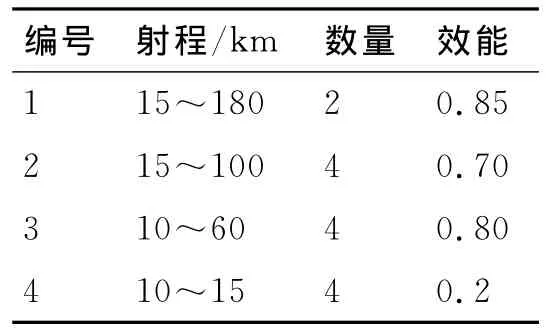
表1 紅方對地武器數據表
紅方武器可用約束矩陣如式(7)所示。
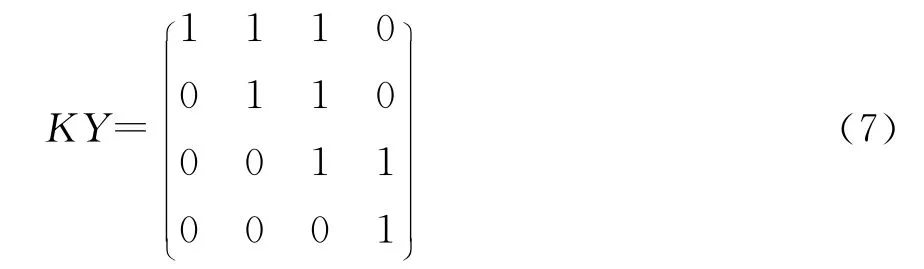
由式(4)可得4種空地武器對地攻擊的協同度矩陣為:
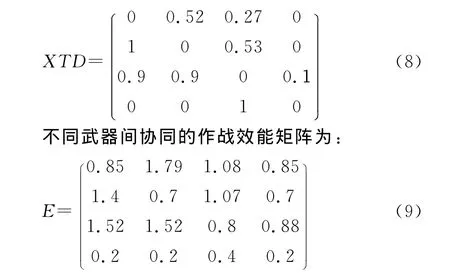
運用動態規劃的方法,求得效能最大的決策矩陣為:

即第1階段不攻擊;第2階段分別發射一枚武器1和2枚武器2;第3階段分別發射一枚武器1、2枚武器2和2枚武器3;第4階段分別發射2枚武器3和4枚武器4。按此方案進行火力協同,攻擊機編隊可取得最大效能E=13.43。
5 結語
本文根據攻擊機編隊機載武器的可攻擊區建立了機載武器間的協同度矩陣,并由此給出了武器間的協同作戰效能計算方法。在一定的作戰想定條件下,運用動態規劃的方法對攻擊機協同突擊地面目標群作戰的數學模型進行了求解,給出了編隊協同突擊的最佳火力運用方案,對進一步探討協同作戰有一定的啟發意義。
[1]沃羅比約夫.俄軍合同作戰原則[M].北京:軍事文藝出版社,1996
[2]許騰.海軍戰術協同論[M].北京:海潮出版社,2004:1~3
[3]軍事科學院.中國人民解放軍軍語[M].1997:90~91
[4]卜先錦.軍事組織協同的建模與分析[M].北京:國防工業出版社,2009,8:10~11
[5]王紅軍,遲忠先.編隊干擾方案協同決策研究[J].系統工程與實踐,2007(4):171~176
[6]白樺,韓文秀.復合系統及其協調的一般理論[J].系統科學與工程研究,2000(9):460~469
[7]呂貴禮,譚安勝.遠程機動岸導與海上編隊戰術協同研究[J].指揮控制與仿真,2009,31(3):21~25
[8]代進進,李相民,孫永芹,等.多編隊對地攻擊協同目標分配算法研究[J].系統仿真學報,2009,21(8):2148~2151
[9]譚安勝.驅護艦編隊對空火力分配環極其復雜性分析與應用[J].軍事運籌與系統工程,2009,23(1):14~18
[10]王紅軍.編隊協同抗導決策關鍵技術研究[D].大連理工大學博士學位論文,2007,2:46~48

