羅蘭C地波傳播的ASF修正研究＊

徐務農 邊少鋒 陳永冰

（海軍工程大學電氣與信息學院1） 武漢 430033）（海軍902廠2） 上海 200083）

1 引言

羅蘭C系統通過測量頻率為100kHz的地波信號從發射臺到用戶接收機之間的傳播時間TOA（圓圓定位）或時間差TD（雙曲線定位）來測定它們之間的距離或距離差，從而實現用戶定位。羅蘭C導航儀的定位解算是建立在地波信號以固定速度（在海水中的傳播速度）、以最短路徑（大圓距離）傳播的假定基礎之上的。由于羅蘭C地波信號的傳播路徑并不是大圓弧，傳播介質也并不全為海水，因此，這兩條假設都帶來了誤差，這種誤差稱為傳播誤差。目前，與傳播路徑有關的傳播誤差成為羅蘭C定位誤差的主要成分。對傳播誤差進行理論和實測研究，對提高羅蘭C的定位精度具有重要的意義。

2 地波傳播時延與ASF

根據電磁波傳播理論，對于任何地波路徑，信號電場的垂直分量可表示為［1］：

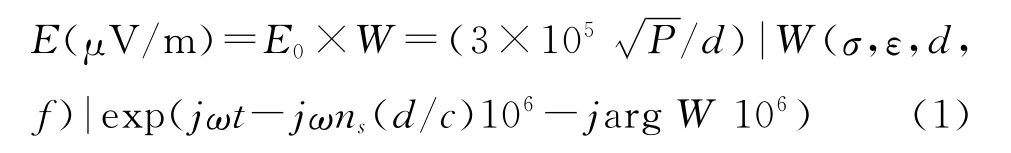
羅蘭C地波信號從發射臺到用戶接收機的傳播時間為：

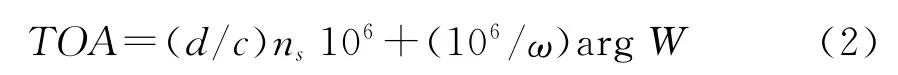
記PF為一次相位因子，即信號在大氣中傳播的時延；SF為二次相位因子，即海水相對大氣的附加時延；ASF為附加二次相位因子，即大地相對海水的附加時延。則PF＝（d／c）ns106，SF＋ASF＝（106／ω）argW，從而

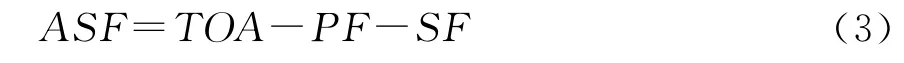
其中，E0為電場的復振幅，對應的相位為一次時延；W為地波衰減函數，對應的相位為二次時延（SF＋ASF）；c為自由空間中的光速（299792.458km／s）；d為 地 波 傳 播 路 徑 的 長 度（km）；ns為沿地波路徑地表面附近大氣折射指數；P為發射天線的輻射功率（kW）；σ為大地電導率；ε為相對大地介電常數；f為羅蘭C信號的頻率。

3 地波衰減函數的計算

由于PF和SF可以準確預算，由式（3）可知，要得到ASF，關鍵是要得到地波信號的傳播時延TOA，而計算傳播時延的核心是求解地波衰減函數。地波衰減函數與地面電導率和相對介電常數以及傳播路徑上大氣折射指數有關，也與地面曲率和地形等因素有關。在工程計算中，按傳播路徑上介質電特性分布和地形高程變化，把傳播路徑分為均勻光滑路徑、分段均勻光滑路徑和非均勻光滑路徑。對于均勻光滑路徑，采用留數級數法計算，近距離用平面模型，遠距離用球面模型。100kHz電波平面模型和球面模型的分界距離取為70km，可以保證兩種模型的計算結果在分界處能夠光滑銜接［2］。對于分段均勻光滑路徑，按電特性和地形特征把路徑分成若干段，用等效電參數法把地形的影響等效為電參數的影響，然后采用米林頓法計算。對于復雜的非均勻光滑不規則路徑，則用積分方程方法來處理。

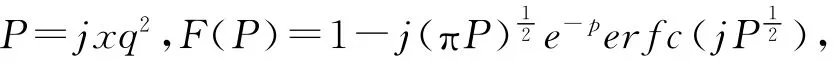
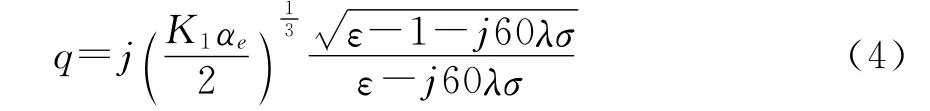
2）｜q｜≤1時，地波衰減函數W的計算公式為：

式中，K1為空氣中的波數2π／λ（1／km）；λ為真空中的波長（m）；ae為等效地球半徑（km）。

3.1 均勻光滑路徑上地波衰減函數的計算

當d＜70km時，地面近似為光滑平面地，按照q絕對值大小采用不同的計算公式。

1）｜q｜＞1時，地波衰減函數W的計算公式為：

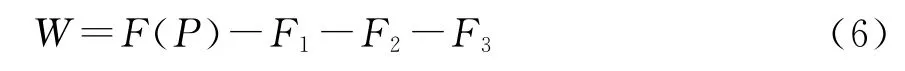
式中，

其中，Am（m＝0，1，…，10）的表達式亦見文獻［2］

當收發兩點距離d＞70km時，將地面視為光滑球面，地表附近的大氣取為標準大氣。參數F用Fock的繞射公式來計算：

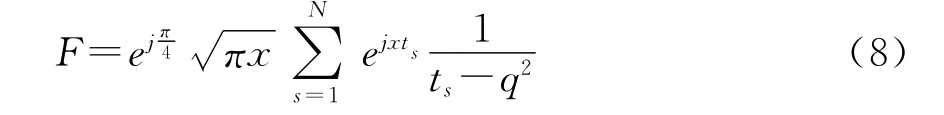
式中，N是一個足夠大的正整數，由級數求和的計算精度而定。由于級數的收斂性，距離越大，級數收斂越快，需要的N越小。這里N無需大于100，就能保證級數的計算精度優于10－6，并可保證與近距離計算結果光滑連續［3］。ts是模方程的第s個復數根。

3.2 分段均勻光滑路徑上地波衰減函數的計算

對于分段均勻光滑路徑，工程計算上多采用米林頓經驗公式。設混合路徑可以劃分為n段，各段地面距離分別為d1，d2，……，dn，大地電導率分別為σ1，σ2，……，σn，相對介電常數分別為εr1，εr2，εm，則混合路徑的地波衰減因子W為：

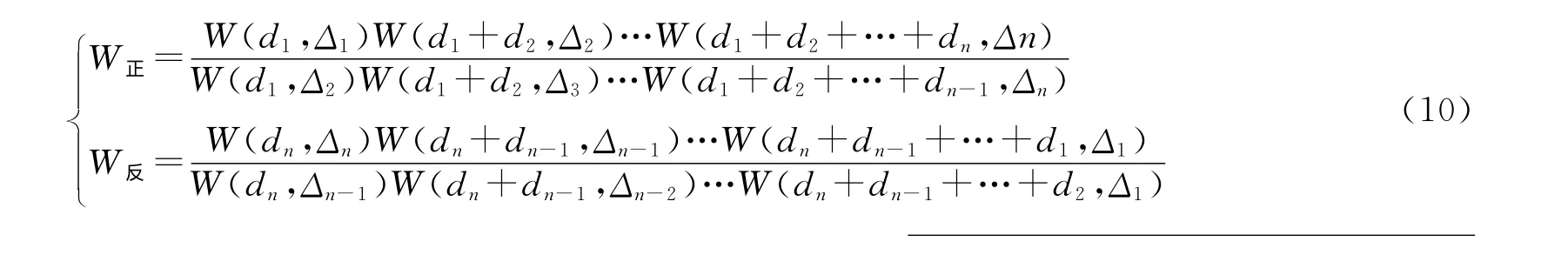
式中，其中，Δi＝Zi／η為第i段路徑上的歸一化表面阻抗，Zi為第i段路徑上的表面阻抗，η為空氣中的波阻抗。W（∑di，Δi）為路徑∑di上，電參數為Δi時，按均勻光滑地球的表達式進行計算的地波衰減因子。

3.3 非均勻光滑路徑上地波衰減函數的計算

當傳播路徑是地面電參數和地形特征都有復雜變化的非均勻光滑不規則路徑時，地波衰減函數需要用積分方程方法進行數值求解。積分方程法的思路是，首先在均勻光滑路徑模型的基礎上，仍然近似地認為垂直電偶極子的赫茲矢量只有垂直于地面的分量，同時應用列翁托維奇近似邊界條件，借助格林定理和收發天線互阻抗概念，得出實際傳播路徑主區地波衰減函數的二維積分方程，然后采用穩定相位法將二維積分方程近似地化為一維積分方程，再用迭代法逐步逼近求解［4～5］。

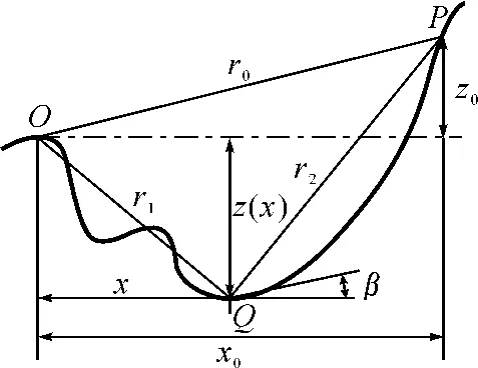
圖1 地形剖面和水平投影示意圖

非均勻光滑路徑的地形剖面示意圖如圖1所示，在不均勻不光滑的地面上有一垂直電偶極子，場源發射天線在地面上的投影點記為原點O，地面上的接收點記為P，地面上任一積分動點記為Q。

非均勻光滑路徑的積分方程推導比較復雜繁瑣，在此只給出接收點處于地面時的一維積分公式［6～7］。

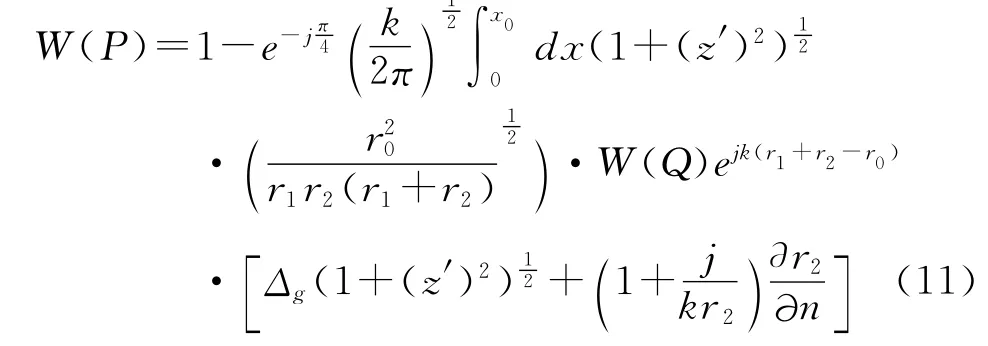
其中，Δg是地面的歸一化表面阻抗。z′是地形標高的導數。

4 地波傳播ASF的測量

圖2 ASF測量框圖

ASF測量系統的組成框圖如圖2所示。用GPS共視法進行時間基準的同步，GPS輸出的1pps秒信號作為TIC（時間計數器）的開門信號，羅蘭C的PCI信號作為關門信號。ASF的測量框圖如圖3所示，圖中有關參量的含義如下［8］：Master Xmit為主臺發射時刻；Station Xmit為副臺發射時刻；Emission Delay（ED）為發射延遲，為固定值；Emission Delay Correction（EDC）為發射延遲修正［9］，由羅蘭 C 管理機構發布；Master Offset from 1PPS為發射時刻與1PPS之間的偏差；Raw TOA為粗TOA，即接收機測得的偽TOA；Predicted All Seawater Path TOA為接收點到副臺之間的路徑為全海水路徑時的TOAsea，即PF＋SF；Received Delay為接收延遲，可精確測得［10］。由圖3，可得到如下關系：

式（13）給出的是副臺的ASF表達式。對于主臺的ASF，表達式為：

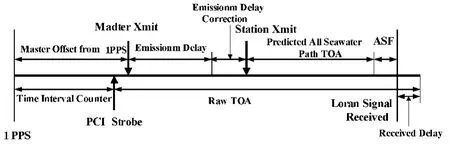
圖3 ASF示意圖

5 計算及實測結果

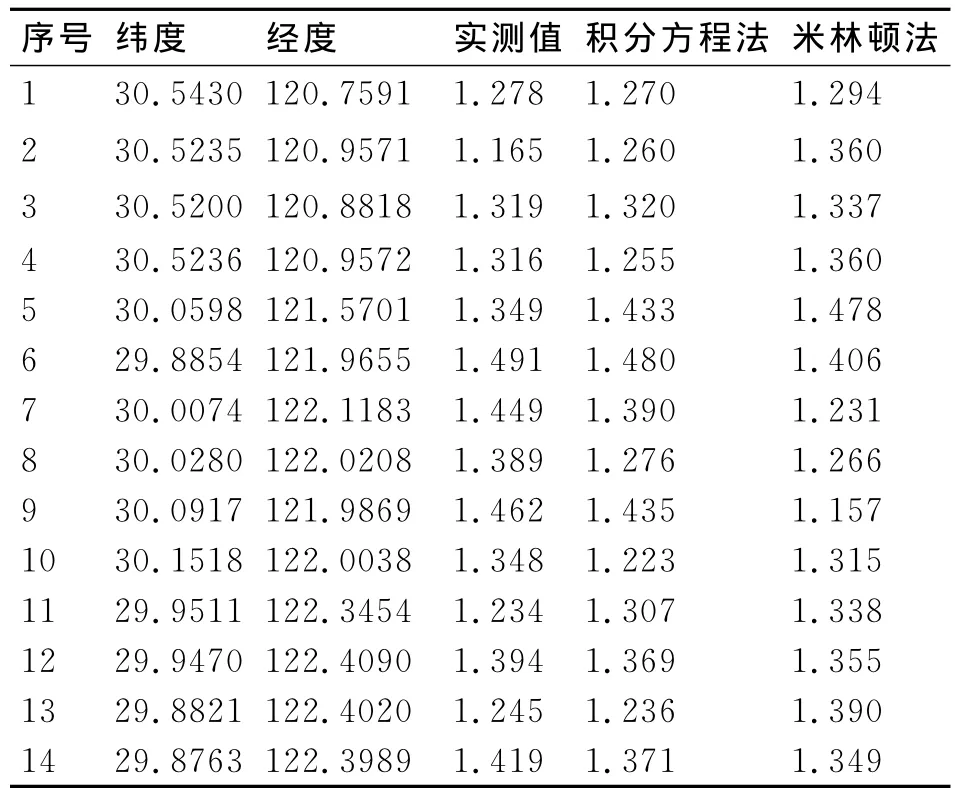
表1 傳播時延實測值與理論計算值比對

表1給出了部分接收點上，用米林頓法和積分方程法計算出的ASF理論預測值和實測值（單位為微秒）。從表中可以看出，用積分方程法比用米林頓法計算出的ASF值更加符合實測的ASF值，這是因為相比于米林頓法，積分方程法可以有效反映地形對地波傳播二次時延的影響。

6 結語

羅蘭C信號地波傳播的ASF修正有理論預測和實測兩種途徑。理論預測法需要羅蘭C信號覆蓋區內的大地電特性數據和大地高程數據以及大氣氣象數據，但ASF的理論預測精度必須經過實際測量的檢驗和修正。ASF的測量不可能在廣闊的覆蓋區內大范圍高密度實施，在實際測量ASF時，如何選擇測量區域、測量線路和測量密度，在一定程度上又需要理論計算來指導。研究表明，采用理論預測和實測修正相結合的方法，建立羅蘭C覆蓋區ASF修正數據庫是可行的，經ASF修正后的定位精度可得到顯著的提高。

［1］海杭.羅蘭C使用手冊［M］.南京：東南大學出版社，1996：33～34

［2］SJ 20839-2002.長波地波傳輸信道計算方法［S］.北京：信息產業部，2002：3～6

［3］潘威炎.長波超長波極長波傳播［M］.成都：電子科技大學出版社，2004：127～129

［4］熊皓.電磁波傳播與空間環境［M］.北京：電子工業出版社，2004：110～117

［5］熊皓.無線電波傳播［M］.北京：電子工業出版社，2000：331～363

［6］王東文.不光滑不均勻地面地波傳播的積分方程方法［J］.電波與天線，1985（4）：21～35

［7］王東文.復雜地面條件下低頻地波傳播的三維預測［J］.電波科學學報，1988，3（1）：50～63

［8］Richard H.A Preliminary Study of LORAN-C Additional Secondary Factor（ASF）Variations［R］.Washington，D.C：Proceedings of the 29st Annual ILA Convention and Technical Symposium，2002

［9］寧民，齊鵬輝，李曉強.羅蘭C發射臺的發射延時測量［J］.導航，2007（1）：43～46

［10］吳海濤.Cs Sync 1000型羅蘭C接收機系統時延的測量方法［J］.電子測量與儀器學報，2002，16（3）：22～27