希爾伯特-黃變換在SAR信號處理中的應用研究*
吳桂生,田 振,察 豪**
(1.海軍軍訓器材研究所,北京102308;2.海軍工程大學,武漢 430043)
1 引言
合成孔徑雷達(SAR)是主動式微波成像雷達,是利用合成孔徑和脈沖壓縮技術以小的真實孔徑天線達到高分辨率成像的雷達系統[1]。近年來,機載和空載SAR 越來越顯示出其在軍事以及民用方面的諸多應用。然而,動目標成像問題是SAR信號處理的一個難題,更是機載SAR 應用必須解決的問題。對于常規SAR 而言,其距離向的高分辨率是通過對線性調頻信號進行脈沖壓縮獲得的,方位向的高分辨率則是通過接受數據與一個理論上的靜止目標進行沖擊匹配相關獲得[2]。實際應用中,成像場景總是包含以前未知方式運動的目標,此時常規SAR的成像方法就不能正常工作,從而造成運動目標圖像的模糊和方位偏移,影響主觀判斷。
顯而易見的是,SAR信號的頻率總是隨著時間連續變化,是一個典型的非線性非平穩信號。對于非線性非平穩信號的檢測而言,聯合時頻分析是解決此類問題的有效工具。傳統的聯合時頻分析方法有很多[3],如短時傅里葉變換(SFTF)、魏格納-威利分布(WVD)、小波變換(WT)等。WVD分布在檢測非線性信號中應用較為廣泛,但是它有著致命的缺點。由于WVD 是雙線性變換,在多點目標檢測或者面目標檢測時,常常出現嚴重的交叉項干擾,從而降低其檢測性能,并且始終存在傅里葉變換的局限性。希爾伯特-黃變換(HHT)是近年發展起來的一種新興的信號處理方法,完全獨立于傅里葉變換。它是從信號自身的角度出發,自適應地對信號進行分解,從瞬時頻率的角度分析信號,與WVD 相比則具有更加準確的譜結構,在分析非線性和非平穩過程中具有很高的應用價值。
本文嘗試利用HHT 對仿真產生的合成孔徑回波信號進行分析,并與WVD 相比較,妥善避免了WVD的交叉項問題,較好地解決了運動目標的檢測問題。
2 HHT的基本原理
HHT 是一種自適應信號處理方法,主要包括兩方面的內容:經驗模態分解 (Empirical Mode Decomposition,簡稱EMD)和希爾伯特譜分析(Hilbert Spectrum Analysis,簡稱HSA)[4],適合于非線性、非平穩信號的分析。它最大的特色是直接對原始信號進行EMD分解,使非平穩信號平穩化,從而使瞬時頻率具有物理意義,進而推導出有意義的希爾伯特時頻譜。HHT 簡單分析流程圖[5]如圖1所示。

圖1 HHT分析流程圖
2.1 經驗模態分解(EMD)
EMD 通常被稱為是一個多次移動的“篩”過程,一方面消除信號上的“騎行波”,另一方面對頻率不一的波形依次進行由高頻到低頻的分解,即將原始信號x(t)自適應地分解成為一系列的本征模態函數(Intrinsic Mode Function,簡稱IMF)以及一個具有單調特性的趨勢項:
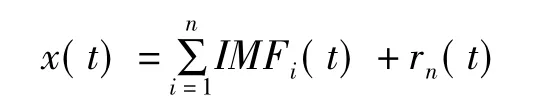
其中rn(t)稱為殘余函數,代表信號的平均趨勢。
對于每一個分解得到的IMF 而言,通常具有如下兩個特性:(1)在整個數據序列中,極值點的數量與過零點的數量必須相等或者至多相差一個;(2)在任一時間點上,信號的局部最大值和局部最小值定義的包絡平均值為零,也就是關于時間軸局部對稱。IMF的上述兩個特性,也是EMD分解終止的依據。需要說明的是,IMF 各階分量是通過EMD 對原始數據自適應分解得到的具有不同尺度特征的波動。因此,它可以是線性的,也可以是非線性的,不影響后續使用。
2.2 希爾伯特譜分析(HSA)
對分解得到的每一階IMFi(t)分量分別作希爾伯特變換,得出各自的瞬時頻率,最終構造希爾伯特時頻譜,即
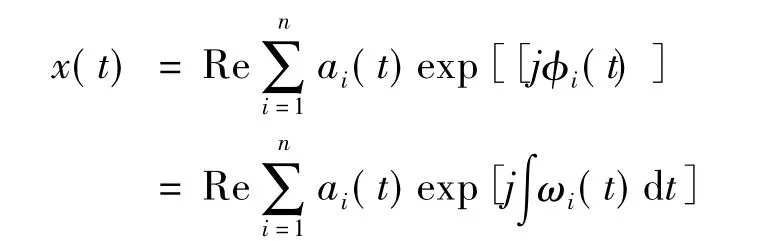
這里省略了趨勢項rn(t),Re為取實部。一般稱等式右端為希爾伯特時頻譜,記作
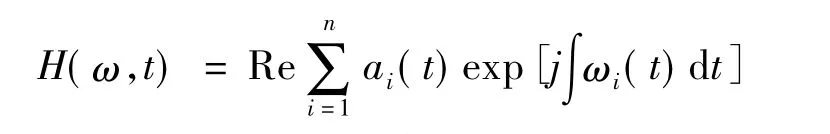
它是瞬時振幅在頻率-時間平面上的分布,瞬時頻率定義為時間的函數。在HHT 二維時頻譜中,振幅大小通常以線條顏色的深淺表示;在HHT 三維時頻譜中,則是以峰值大小表示其在某時刻以及瞬時頻率上的能量大小。
3 HHT 檢測目標方法
HHT 是一種新興的時頻分析方法,檢測目標的主要方法是利用目標的時頻譜圖,分析瞬時頻率的能量分布,進而確定有無目標。具體思路如下:
(1)首先對原始信號通過經驗模態分解得到一系列從高階到低階的瞬時頻率曲線,并作圖;
(2)將這些瞬時頻率曲線通過二維時頻譜進行顯示,依據得到的二維時頻譜圖分析各階瞬時頻率的能量大小,在二維時頻譜中,能量大小通常依據線條顏色的深淺為依據;
(3)依據各階瞬時頻率的能量大小判斷目標是否存在以及存在于哪一條或者幾條瞬時頻率曲線中,然后對選擇的瞬時頻率曲線進行三維作圖,具體判斷目標在瞬時時刻及瞬時頻率下瞬時振幅的大小,確定目標的相關參數。
例如:仿真生成一個512 點單分量信號,如圖2所示。利用上述HHT 檢測目標原理進行仿真作圖,檢測該單分量信號的存在。
圖3 是通過EMD分解得到的從高階到低階依次排列的IMF分量。顯然,只有IMF1、IMF2為有效分解量,其余皆有EMD分解的不徹底性導致,可以不作考慮。故在圖4中只需做出IMF1、IMF2的二維時頻圖即可,在圖5 三維時頻圖中明顯觀察出該單分量信號的存在,驗證了HHT 檢測目標方法的有效性以及可行性。
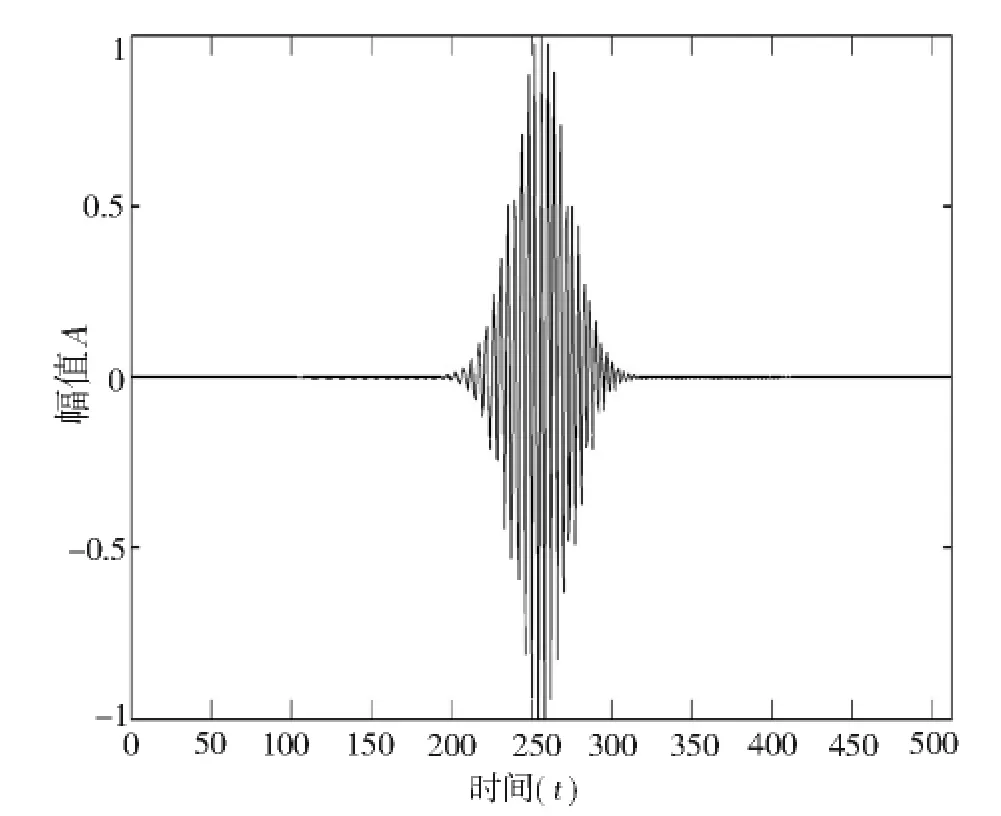
圖2 單分量信號
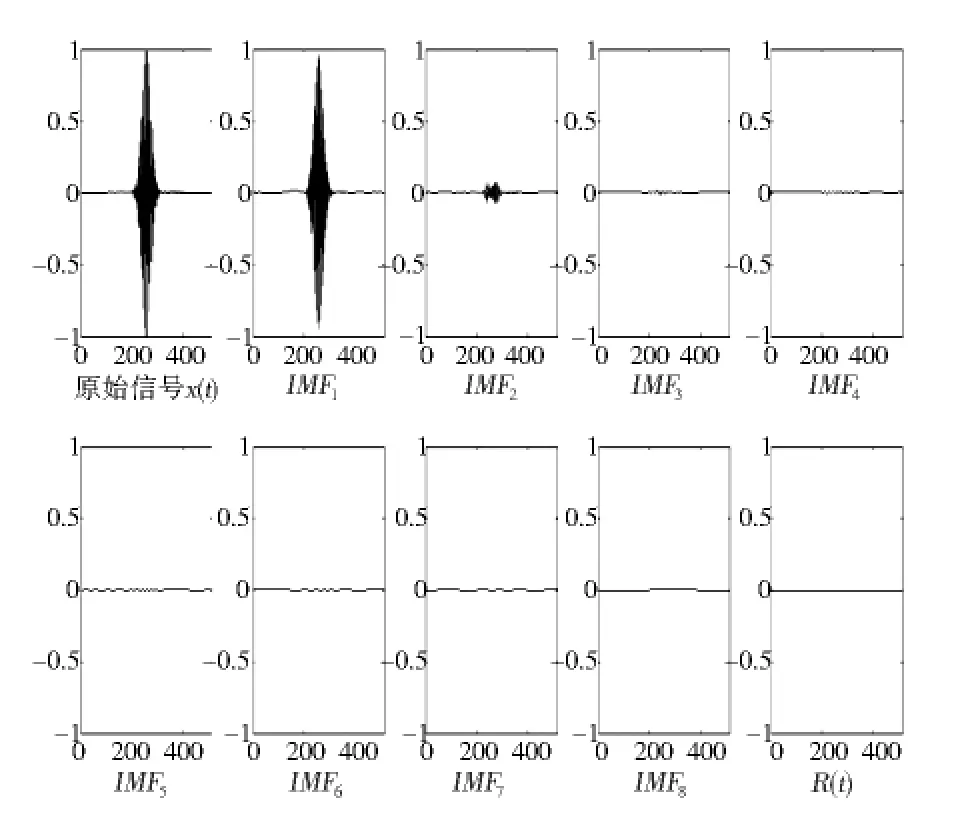
圖3 EMD分解得到的各IMF分量

圖4 二維時頻譜圖
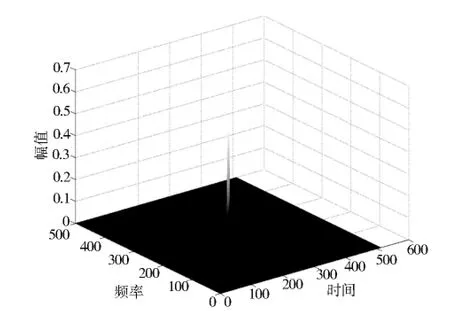
圖5 三維時頻譜圖
4 HHT 在SAR信號處理中的具體應用
在上節中驗證了HHT 檢測目標的方法,現在將利用此方法檢驗頻率時變的合成孔徑回波信號中的目標存在,驗證HHT 在SAR信號處理中的可用性。
通過數據仿真生成兩段不同的合成孔徑回波信號的實部波形,如圖6(a)、(b)所示。這兩段回波數據均是理想情況下(無背景噪聲)仿真生成的SAR 回波信號,從圖中難以分辨目標的存在,只能隱約察覺波形的頻率始終隨著時間變化,是一段明顯的非線性非平穩信號。在這里,將分別利用WVD和上述HHT 目標檢測方法對該段數據進行處理,分析比較二者性能。
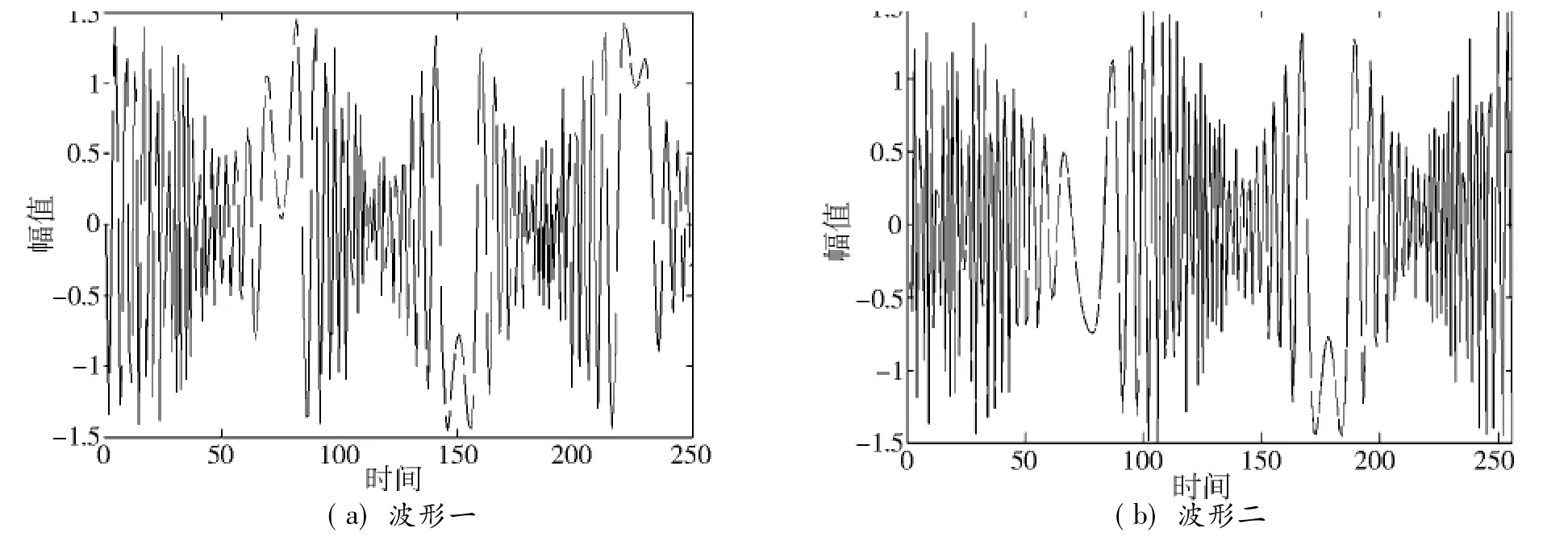
圖6 SAR 回波信號的實部波形
圖7(a)、(b)是對兩段波形分別作二維時頻譜圖。從圖中可以明顯看出,瞬時頻率大致隨正弦變化,呈現明顯的非線性特征。故選擇圖中能量最大的一段瞬時頻率曲線進行三維作圖,如圖8(a)、(b)和圖9(a)、(b)所示,進而判斷目標的存在與否以及相關參數。
比較圖8和圖9發現,通過HHT 作出的三維時頻譜圖相較于WVD 而言,二者都能夠檢測出目標的存在,能夠大致確定目標的相關參數。除此之外,HHT 比WVD 有更好的能量聚集性,這對于判斷目標相關參數的準確性有著十分重要的作用。但是,HHT 三維時頻譜中“旁瓣”較多,需要通過嚴格的數據處理以消除“旁瓣”,且受到邊界效應的影響,需要進行合適的邊界延拓以消除邊界效應。
通過與WVD的比較,可以發現,HHT 同樣可以運用于SAR信號的目標檢測,驗證了HHT 在SAR信號處理中的可用性,并且具有更好的能量聚集性。
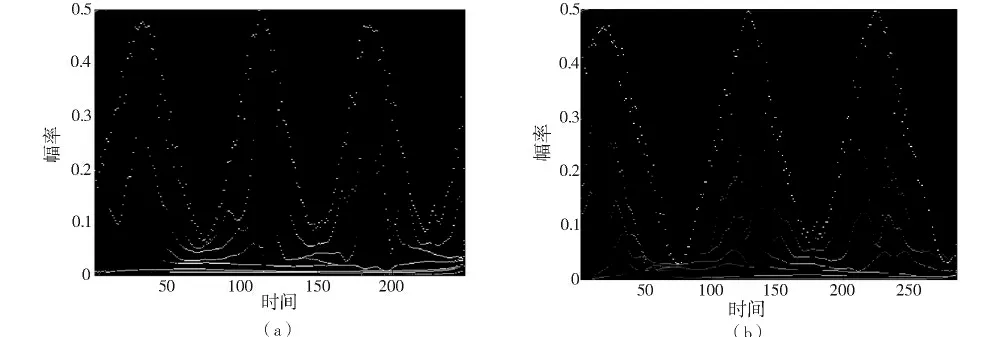
圖7 各階瞬時頻率的二維時頻譜圖
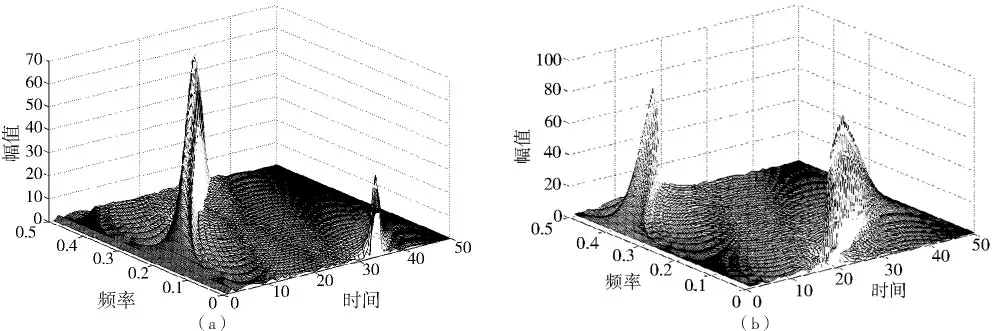
圖8 WVD 三維時頻譜
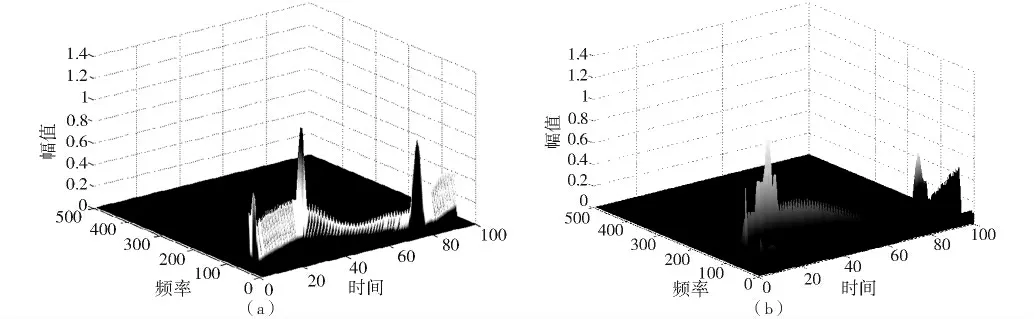
圖9 HHT 三維時頻譜
5 結束語
本文主要介紹了HHT的基本原理以及檢測目標的方法,最后應用于SAR信號處理中。研究表明,擺脫了傳統傅里葉變換的束縛,克服了WVD的交叉項干擾,可以如同WVD 那般利用時頻譜圖檢測出SAR信號中目標的存在,且具有更好的能量聚集性。不足之處在于,HHT 理論發展還不夠成熟,有著嚴格的使用條件,需要在實踐中加以總結,相信在不久的將來一定能發展成為一種行之有效的信號處理方法,在更多領域發揮重要作用。
[1]N E Huang,Samuel S P Shen.Hilbert-Huang Transform and its applications[M].World Scientific Pressing,2005:289.
[2]張明友,汪學剛.雷達系統(第二版)[M].北京:電子工業出版社,2006.
[3]葛哲學,陳仲生.Matlab時頻分析技術及其應用[M].北京:人民郵電出版社,2006.
[4]Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceeding of the Royal Society,London,1998,454 (A):903-965.
[5]殷曉中,于盛林.希爾伯特-黃變換理論及其應用探討[J].鎮江高專學報,2007,20(2),31-34.
[6]Hans S.Hilbert Transforms in Signal Processing[C].Artech House,1995:442.
[7]沈毅,沈志遠.一種非線性非平穩自適應信號處理方法——希爾伯特-黃變換綜述:發展與應用[J].自動化技術與應用,2010,29(5):1-5.

