一種調頻連續波距離-速度配對處理方法*
潘勇先,朱子平
(華東電子工程研究所,合肥 230088)
1 引言
線性調頻連續波(Linear Frequency-Modulated Continuous Wave,LFMCW)雷達具有體積小、重量輕、結構簡單、分辨力高和無距離盲區等優點,但受到處理方法的限制以及調頻線性度的影響,通常只能應用于近程測距系統中。另外,單一調頻斜率的LFMCW信號存在距離-速度耦合現象,將導致運動目標的測距偏移問題。該問題可通過采用對稱LFMCW信號加以解決,但同時也引入了多目標環境下的配對問題[1-2]。
本文通過研究線性調頻連續波雷達的信號處理,提出了一種三角調頻連續波雷達目標差拍幅度譜中心頻率幅度譜值配對方法來校正多普勒頻率造成的測距誤差,并給出了計算機仿真結果。
2 基本原理
設雷達發射線性調頻連續波信號,雷達載頻為f0,調頻帶寬為B,調頻間隔為T,正向調制和負向調制交替發射,視頻信號的頻率與時間關系如圖1所示。圖1中,發射信號用細實線表示,目標回波信號用粗實線表示,有多普勒頻率時的目標回波信號用粗虛線表示[3-4]。
在上掃頻段周期內,線性調頻連續波雷達發射信號在有效區間Te,up=[-T/2,T/2]可以表示為
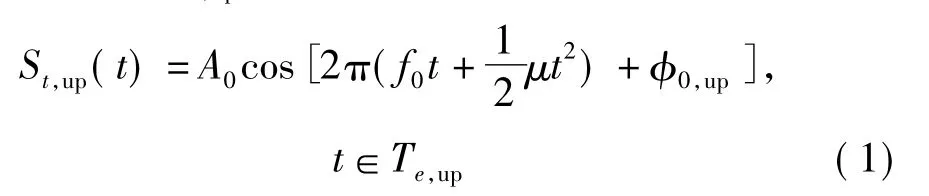
其中,f0、A0和φ0,up分別代表發射信號的頻率、振幅和隨機初相,μ=B/T為調頻斜率。
一個勻速運動目標,以徑向速度v 接近雷達(以遠離雷達方向為正方向),在t=0時刻目標斜距為R0,回波延遲為τ(t),多普勒頻率為fd=2v/λ,則接收到的目標回波信號Sr,up(t)在有效區間Te,up(t)內可以表示為
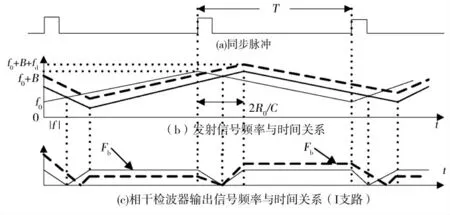
圖1 三角調頻連續波雷達頻率時間關系
其中,常量Kr與目標反射強度和傳播衰減有關,φ0,up代表目標反射引起的附加相移,τ(t)=2(R0+vt)/c為目標的延時函數。
對差拍信號進行傅里葉變換:
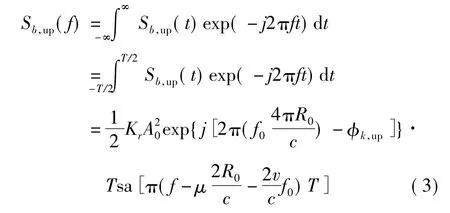
其中sa 是辛克函數。同理可以證明,在發射信號一個掃頻周期內,三角線性調頻信號下掃頻段頻譜為

線性調頻連續波雷達上掃頻段差拍信號的回波中心頻率為fb,up=2μR0/c+2vf0/c,線性調頻連續波雷達下掃頻段差拍信號的回波中心頻率為fb,down=-2μR0/c+2vf0/c-μ2vT/c。當fd=0時,正向調制和負向調制回波差拍信號的中心頻率大小相等、符號相反,不會引起測距誤差;當fd≠0時,會引起測距誤差,正負向調制回波信號的測距誤差大小相等、符號相反。如果能夠估計出正負向調制回波信號的中心頻率,則取二者的平均值就可以消除測距誤差,困難在于如何判斷正負向調制的回波為同一目標所產生。下面針對這一問題提出頻譜配對方法。
3 頻譜配對方法
由式(3)、(4)知同一目標的正向調制段和負向調制段產生的差拍信號頻譜Sb,up(f),fb,down(f)具有相同的幅度和形狀,在實際應用環境中由于目標起伏及天線掃描等多方面的影響,可能會出現兩個頻譜的幅度不完全相同的情況。但是,同一目標產生的回波頻譜的幅度在正/負調制段總是具有最大的相似性。根據這一點就可以在正/負調制段分別得到的差拍信號頻譜中找到同一個目標產生的譜線。
這里采用的方法是尋找差拍幅度譜中心頻率對應的幅度譜之值,相同目標產生的差拍幅度譜中心頻率對應的幅度譜值積總是相近的。設第M個目標在正向調制階段產生的差拍信號幅度譜采樣值序列為{ SM,up(1),SM,up(2),…,SM,up(n)},中心頻率對應的幅度譜值為

其中△f為頻域采樣間隔。負向調制段差拍信號幅度譜中心頻率對應的幅度譜值為
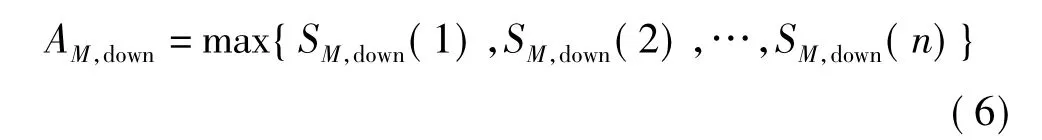
由前面分析可知,AM,up和AM,down的值最接近。由式(5)、(6)求出N個目標的差拍幅度譜中心頻率對應的幅度譜值矩陣A:

正向調制段各個差拍幅度譜中心頻率幅度譜值與負向調制段各個目標差拍幅度譜中心頻率幅度譜值的差矩陣△A為

其中△A(i,j)=△A(i,up)-△A(j,down)。
對于正向調制段的第i個差拍回波幅度譜中心頻率對應的幅度譜值差向量△Ai,i=1,2,…,N,如果△A(i,k)是向量中最小的,那么可以認為正向調制段中的第i個差拍回波和負向調制段中的第k個差拍回波是由同一個運動目標產生的。
4 測量誤差校正
對于運動目標1,設其頻譜配對后的正負向調制回波頻率為f1,up和f1,down,由前面的分析知目標實際距離對應的差拍頻率為
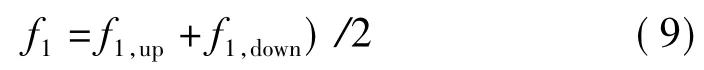
對應的距離為

通過上/下掃頻段的頻率差可以得到目標1的多普勒頻率f1,d=(f1,up+f1,down)/2,又因為fd=2v/λ(λ=c/f0),所以目標1的徑向速度為
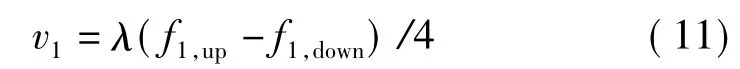
通過式(10)和(11)就可以確定出目標1的真實距離和徑向速度。
用同樣的方法可以得到其他N-1個目標的真實距離和運動速度。這樣就能成功地將一個距離段中不同距離不同速度的目標區別開來,從而消除了線性調頻連續波雷達的距離-速度耦合。
5 計算機仿真
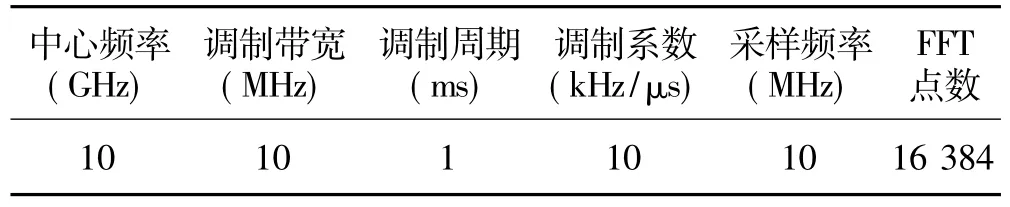
表1 仿真系統參數
計算機模擬的系統參數如表1所示。設在距離為4 000 m和9 000 m處有兩個運動點目標,速度分別為-200 m/s,-130 m/s(向雷達方向運動為負),回波幅度分別為0.8和0.5;在5 000 m處有固定點目標,回波幅度為1.2。正負調制回波差拍信號16 384點FFT的頻譜如圖2(a)、(b)所示。
在圖2(a)中按照譜峰的頻率由小到大排列分別稱為目標1+,目標2+和目標3+;在圖2(b)中按照譜峰的頻率由小到大排列分別稱為目標1-,目標2-和目標3-,計算出差拍頻譜中心頻率對應的幅度譜值和值的差見表2、3和4。
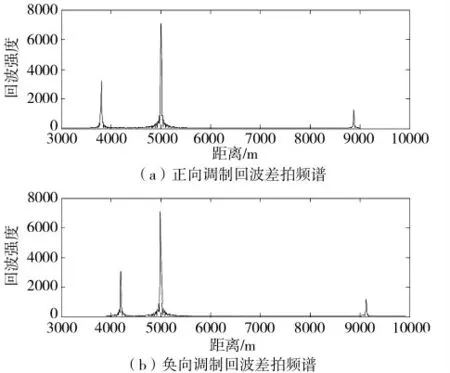
圖2 目標回波差拍信號頻譜

表2 回波差拍頻譜中心頻率頻譜值(正向調制)

表3 回波差拍頻譜中心頻率頻譜值(負向調制)

表4 回波差拍頻譜中心頻率頻譜差值
按照幅度譜差值最小的原則配對為:目標1+和目標3-配對;目標2+和目標2-配對;目標3+和目標2-配對。
按照式(10)和(11)校正后的目標距離和速度見表5。仿真結果是在不同信噪比下進行的,表6 說明了在不同信噪比下配對結果的正確性。
從表5 可以看出,利用上下掃頻段的頻譜的相似性,采用頻譜最大峰值配對算法可以獲得目標的距離和速度。根據理論分析知道,在兩個目標回波的幅度差別不大時,可能會造成頻譜配對錯誤。在仿真中發現,當兩個目標回波幅度相同或相近時,還是可以通過上面的方法進行頻譜配對而不出現錯誤。但是,該方法的目標配對單靠上下掃頻頻譜峰值來確定,對處于同一距離而具有不同速度的目標將出現較大的測距誤差,對于高密度目標的情況較難配對成功,而且運算量很大,難適應大量目標的場合。由于目標運動有可能出現目標距離譜重疊,也可能造成頻譜配對錯誤。這些尚需進一步的分析。

表5 校正后的目標距離和速度

表6 不同信噪比下仿真結果正確性
6 結束語
按照正負相間頻率調制連續波雷達回波差拍信號的頻譜特點,提出了一種目標回波頻域配對及連續波雷達多普勒測距誤差校正的方法。理論分析和仿真實驗結果表明,該方法能夠有效地校正多普勒效應引起的距離測量誤差。
[1]徐小平,劉建新,等.FMCW測距雷達數字信號處理器設計仿真[J].信息與電子工程,2004.6.
[2]史林,張琳.調頻連續波雷達頻譜配對信號處理方法[J].西安電子科技大學學報,2003,30(4):534-538.
[3]包敏.線性調頻連續波雷達信號處理技術研究與硬件實現[D].西安電子科技大學碩士論文,2009.1.
[4]馬曉巖,向家彬,等.雷達信號處理[M].湖南長沙:湖南科學技術出版社,1999.

