一種基于可移動錨節點的DV-HOP改進定位算法
胡 淼,陶正蘇
(上海交通大學 電子信息與電氣工程學院,上海 200240)
無線傳感器網絡是將大量傳感器隨機布設到某一目標區域,以無線的方式進行通信,并將采集到的數據在全網中進行傳輸,以實現對目標區域的監測。傳感器的位置信息對監測活動至關重要,沒有位置信息的的監測消息往往是沒有意義的,而且無線傳感器網絡中的許多路由協議和運用都是在位置信息已知的前提下設計的,因此傳感器的定位是傳感器網路的關鍵技術之一。
無線傳感器網絡定位技術有許多種,大致可以分為基于距離定位和距離無關定位兩類。基于距離的定位主要是通過測量傳感器節點之間的距離或角度實現對未知節點的定位,TOA、TDOA、RSSI和AOA等是常見的基于距離的定位算法,這類定位算法對收發節點間的時間性有嚴格要求,對硬件條件要求較高,但定位精度相對較高;距離無關定位利用網絡內部連通性來實現對未知節點定位,質心算法、DV-Hop、Amorphous和APIT等是常見的距離無關算法。其中,DV-Hop算法具有易實現,對硬件要求低等特點。但是,錨節點分布不均的情況下,DV-Hop具有較大的定位誤差,針對DV-Hop的這一缺陷,提出了一種基于可移動錨節點的DV-Hop定位算法,并通過仿真實驗對兩種算法性能進行比較。
1 DV-Hop算法及其改進
1.1 DV-Hop算法
Niculescu等人首次在文獻中提出了DV-Hop定位算法,類似傳統網絡中的距離向量路由機制,DV-Hop定位過程可以分為3個步驟:
第1步,計算未知節點與每錨節點的最小跳數。
錨節點向鄰居節點廣播自身位置信息分組,其中包括跳數字段,初始化為0。接收節點只記錄到每個錨節點最小跳數,并將跳數字段加1轉發給鄰居節點。由此,所有節點記錄下到每個錨節點的最小跳數。
第2步,計算錨節點與信標節點的實際跳段距離。
每個錨節點根據第一步中其他錨節點的位置信息和相距跳數,利用公式(1)估算平均每條距離:

其中(xi,yi),(xj,yj)是錨節點 i, j的坐標,hj是錨節點 i與 j的之間的跳數。錨節點再將計算的每跳平均距離用帶有生存字段的分組廣播到全網中,未知節點只記錄收到的第一個每條平均距離,并轉發給鄰居節點。未知節點根據記錄的每跳平均距離以及第一步當中的跳數計算到每個錨節點之間的跳段距離。
第3步,未知節點根據到各個錨節點的跳段距離值,利用三邊測量法或極大似然估計法計算未知節點的坐標。
當所有錨節點到未知節點P的距離d已知時,可按式(2)進行計算:
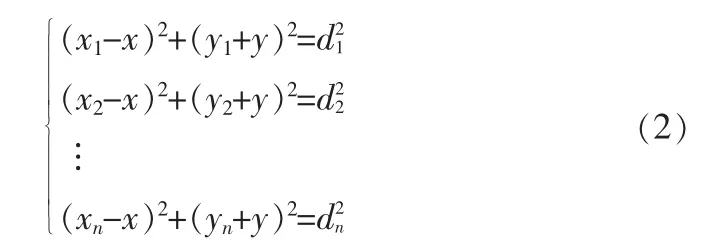
可由式(2)可得線性方程組:

對式(3)使用標準的最小均方誤差估計方法可以得到節點的坐標為:

1.2 基于移動錨節點DV-Hop算法
DV-Hop是一種典型的與距離無關定位算法,其誤差主要產生于利用錨節點計算出來的平均每跳距離來代替全局平均每跳距離,為減小誤差就要求錨節點能夠盡量均勻的分布在被測區域中,使錨節點平均每跳距離更接近全局平均每跳距離。針對這一特點,文獻[4]提出了一種基于可規律移動錨節點定位算法RRDV-Hop,RRDV-Hop利用一個規律移動的錨節點近似的構建出N個均勻分布于網絡的錨節點,提高了定位精度。文中參考文獻[4]的思路,在假設所有的錨節點都有一定移動能力的基礎上,提出了基于移動錨節點DV-Hop定位算法 MAN-DV Hop(Mobile Anchor Node-DV Hop)。
MAN-DV Hop設定所有的錨節點都具有一定的移動能力,在所有節點隨機部署在監測區域后,錨節點會與通信范圍內的其他錨節點產生一種虛擬力(virtual force),而錨節點會根據虛擬力的大小及方向計算出自身位置的修正值,并移動到相應位置,實現錨節點的重新部署,使所有的錨節點能夠均勻的分布于整個網絡當中。然后MAN-DV Hop根據錨節點的新位置計算平均每跳距離,再完成未知節點的定位。
1.3 錨節點間虛擬力模型
為了使錨節點更均勻的分布于整個監測區域,可假設相隔較近的錨節點間會產生一種虛擬力,使錨節點移動到合適位置,直到虛擬力弱化為0。在傳感器網絡中,節點見常構建的虛擬力模型主要有4種。第1種虛擬力定義:
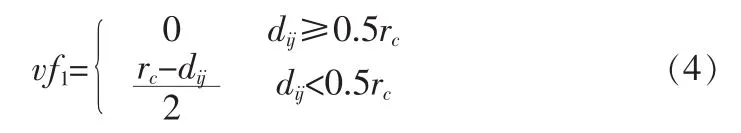
式(4)中dij表示錨節點i和j之間的距離,rc為節點通信半徑,當兩個錨節點間的距離超過0.5rc時,錨節點間不在產生虛擬力。
參考電荷之間庫倫力模型,可以得到第2種虛擬力定義:
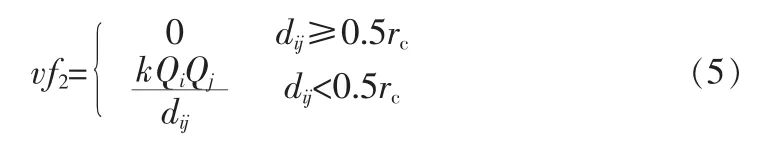
式(5)中 Qi,Qj原本表示兩個電荷所帶的電量 i,j而在傳感器網絡中可用,節點的網絡連通度來代替。
第3種虛擬力定義為:
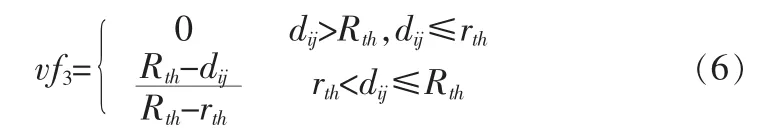
式(6)中有兩個距離閾值rth與Rth,dij表示兩節點之間的距離,rth與Rth的變化將影響錨節點對監測區域的覆蓋率。
第4種常見的虛擬力定義為:

式(7)中wA表示虛擬力的引力系數,wR表示虛擬力的斥力系數,利用wA,wR可調節錨節點重部署后的疏密度。文獻[5]分析了4種模型中各個參數對網絡覆蓋率的影響,MAN-DV Hop可根據不同節點分布情況選定不同的虛擬力模型。
當錨節點受到通信范圍內其他錨節點產生虛擬力后,由原位置(x0,y0)更新到新位置(xnew,ynew),轉化模型為:

式(8)中,Maxstep是傳感器節點的最大移動距離,Fxy是作用于傳感器節點的虛擬力,Fx,Fy分別是虛擬力在X軸和Y軸方向上的分量,Fth是設定的虛擬力閾值,當兩個錨節點間的虛擬力絕對值小于閾值時,錨節點不發生移動。
1.4 虛擬力模型的選定
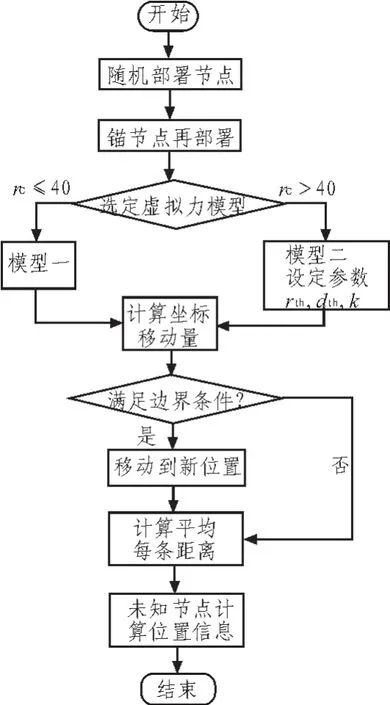
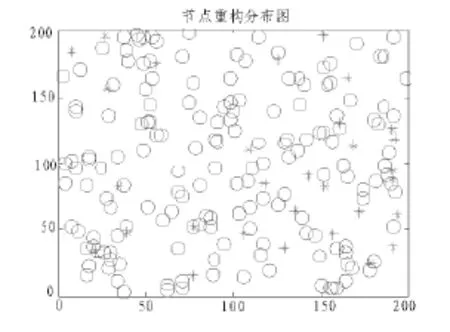
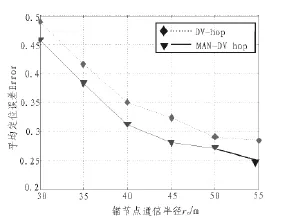
文獻[5]分析了4種虛擬力的參數對模型性能的影響,其中用來評定模型性能的指標包括:覆蓋增加率,覆蓋效率,平均移動距離。模型一結構簡單,且錨節點間的虛擬力只是斥力。當節點的通信半徑較小時,MAN DV-hop選取模型一作為錨節點間的作用力,改善錨節點分布過于密集時的情況。當錨節點通信半徑較大時,模型一中虛擬力大小與通信半徑成正比rc,錨節點間斥力過大,使計算的平均每跳距離偏離真實值。當傳感器節點通信半徑較大時,網絡的平均每跳值Hopsize 式(9)中a,b為小于1的范圍系數。由此,綜合模型1、模型3、模型4MAN DV-hop構建虛擬力模型: 式(10)表明,當量錨節點間的距離時 dij∈(rth,Rth),MANDV Hop認為此時錨節點間的距離分布是合理的,此時錨節點間不產生虛擬力作用 。當錨節點間的距離dij∈(0,rth)∪(Rth,rc)時,MAN DV-Hop認為節點間的距離過短或者過長,節點間產生虛擬力作用,且dij∈(0,rth)虛擬力為斥力,dij∈(Rth,rc)時,虛擬力為引力。 式(10)中 k1表示斥力系數系數,k2表示引力系數,用來控制虛擬力作用的強弱。 由于MAN-DV Hop設定錨節點具有一定的移動能力,并在虛擬力的作用下移動到新的位置。對于初始隨機分布在監測區域邊界的錨節點,經過移動后錨節點可能越過監測區域的邊界或大部分通信范圍不在監測區域內。式(8)中設定了錨節點的最大移動距離Maxstep,若錨節點初始位置是(xo,yo),MAN-DV Hop 需判斷(xo±Maxstep,yo±Maxstep)是否處于監測區域內。MAN-DV Hop算法流程圖如圖1所示。 圖1 MAN DV-Hop定位算法流程圖Fig.1 Flow chart of MAN DV-Hop algorithm 為了驗證MAN-DV Hop算法的性能,采用Matlab進行仿真實驗。在仿真實驗中,假設所有節點都隨機分布在一個20 m×200 m的二維平面上,在該區域內隨機放置200個節點,未知節點的通信半徑為rc,錨節點攜帶GPS定位設備,因此錨節點的坐標位置是已知的,并且錨節點具有一定的移動能力。仿真通過計算未知節點的定位坐標與實際坐標之間的平均誤差與節點通信半徑的比值來評定定位精度的高低,節點平均定位誤差率: 式(11)中,erri表示節點i的定位誤差,un表示未知節點數量,rc表示節點的通信半徑,Error值越大,表示定位誤差越大,Error值越小,表示定位的精度越高。 設定節點通信半徑rc=30 m,Maxstep=10 m,錨節點數量為30,此時MAN-DV Hop選定虛擬力模型一 ,仿真實驗中網絡節點初始分布圖如圖2所示。 圖2 節點分布圖Fig.2 Node distribution chart 錨節點重部署后的分布圖如圖3所示。 圖3 錨節點重構分布圖Fig.3 Anchor node re-distribution chart 圖中o表示未知節點,*表示錨節點。比較圖2,圖3可得錨節分布變化情況。通過計算,初始分布時的網絡平均聯通度為12.29,網絡的鄰居錨節點平均數目為1.775。當錨節重部署后,網絡的平均連通度為12.5,網絡的鄰居錨節點平均數目為1.92。當錨節點通信半徑rc=50 m時,虛擬力模型設定為二,k1-k2=10,Rth=0.8rc,rth=0.2rc初始分布時的網絡平均聯通度為29.93,網絡的鄰居錨節點平均數目為4.2。當錨節重部署后,網絡的平均連通度為30.53,網絡的鄰居錨節點平均數目為4.585。結果表明傳感器節點在經過網絡初始隨機部署后,錨節點發生移動重部署后,錨節點的分布情況趨于均勻。 設定節點通信半徑rc由30 m變化到60 m,步長為5 m。Rth=0.8rc,rth=5 m,Maxstep=10 m,k1-k2=5 節點平均定位誤差變化情況: 圖4 平均定位誤差對比圖Fig.4 Average location error chart 設定通信半徑rc=30 m,錨節點比例由10%變化到60%,步長為5%時,平均定位誤差的變化情況: 圖5 平均定位誤差對比圖Fig.5 Average location error chart 由圖4,圖5可知,在相同的網絡條件下,MAN-DV Hop具有更高的定位精度。 文章在DV-Hop定位算法的基礎上,設定錨節點具有一定的移動能力,通過構建錨節點間的虛擬力來使其移動,使錨節點更均勻的分布于整個網絡,從而提高了DV-hop定位算法 的定位精度。仿真結果表明,相同條件下,隨機分布的網絡中,與DV-hop算法相比,MAN DV-hop算法降低了平均定位誤差,并且定位精度更穩定。 [1]孫利民,李建中,陳渝,等.無線傳感器網絡[M].北京:清華大學出版社,2005. [2]Niculescu D,Nath B.DV based positioning in Ad hoc networks[J].Telecommunication Systems,2003(22):267-280. [3]Bulusu N,Heidemann J,Estrin D.GPS-less low cost outdoor location for very small devices[J]. IEEE Personal Communications,2000,7(5):28-34. [4]李瑞雪,房至一,儀婷婷.基于可規律性移動錨節點和接收信號強度指示器的改進DV-Hop定位算法及其性能分析[J].吉林大學學報,2011,41(2):435-441.LI Rui-xue,FANG Zhi-yi,YI Ting-ting.Improved DV-Hop localization algorithm based on regularly moving anchor(RMAN)and received signal strength indicator (RSSI)and its performance analysis[J].Journal of Jilin University,2011,41(2):435-441. [5]任孝平,蔡自興,任清雄.四種虛擬力模型在傳感器網絡覆蓋中的性能分析[J].信息與控制,2010,39(4):441-445.REN Xiao-ping,CAI Zi-xing,REN Qing-xiong.Performance analysis four virtual force models used for coverage algorithm of wireless sensor networks[J].Information and Control,2010,39(4):411-445. [6]王雪,王晟,馬俊杰.無線傳感網絡的虛擬力導向微粒群優化策略[J].電子學報,2007,35(11):2038-2044.WANG Xue,WANG Sheng,MA Jun-jie.Dynamic sensor deployment strategy based on virtual forcev directed particle swarm optimization in wireless sensor networks[J].Acta Electronica Sinica,2007,35(11):2038-2044.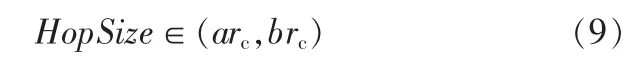

1.5 邊界條件
2 仿真驗證
2.1 參數設置與誤差指標

2.2 算法仿真與分析


3 結 論

