改進的非相干信號子空間寬帶測向算法

宮 兵,徐以濤,李 佳

(解放軍理工大學通信工程學院,江蘇南京210007)

0 引言

寬帶信號是電子偵察常見信號之一,對其進行測向是電子偵察的主要任務[1]。近年來有關寬帶源方位的估計愈來愈受到人們的關注。非相干信號子空間方法[2](ISM)是最早提出的寬帶信號的測向算法,其思想是通過頻域變換將時域信號分解成不同頻率的子帶,在每個子帶上分別應用窄帶信號測向算法,然后再對不同子帶的測向結果進行平均得到寬帶信號的方位估計。由于在某些子帶信號的功率會非常低導致這些子帶的會對最終測向結果造成較大的誤差,從而影響測向精度。為此文獻[3]提出了基于聚焦變換思想的相干信號子空間算法(CSM),其中聚焦矩陣的求解是算法的關鍵。隨后文獻[4]等文獻分別介紹了幾種不同的聚焦矩陣的求解方法對CSM算法進行改進,然而聚焦矩陣的計算也是不小的計算量。這里提出了一種基于最大功率進行頻點選擇的改進的ISM算法,稱為MISM算法,它不需要像ISM算法在每個頻點都要進行窄帶信號測向算法,也不需要像CSM算法進行聚焦矩陣的計算,大大減小了運算量,提高了測向精度。

1 陣列結構和信號模型

考慮有m個陣元的均勻線陣,陣元間距為p,令左邊第一個陣元為參考陣元,如圖1所示。

假設有d(d＜m)個遠場寬帶不相干信號進入陣列,其到達角分別為 θ1,…,θd,并假設信號和噪聲具有相同的帶寬B,并且陣元輸出噪聲是空時統計獨立的、零均值的和方差為 σ2的高斯白噪聲,且與信號不相關。于是,第i個陣元上接收的信號可表示為:

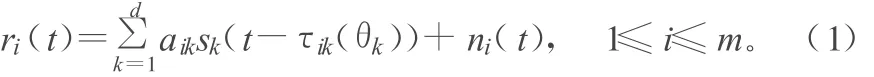
式中,sk(?)為在任意參考點接收的由第k個信源發射的信號;τik為第i個陣元對第k個信源的傳播延遲;aik為第i個陣元對第k個信源的幅度響應;ni(?)為第i個傳感器上的加性噪聲。對于均勻線陣,傳播延遲可表示為:

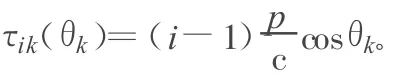
式中,c為傳播速度。因為sk(?)為寬帶過程,所以在頻域表述這一問題更方便。假設觀測時間間隔為T,ri(t)可用傅里葉系數表示為:

式中,Ri(ωn)為傅里葉系數,表示為:

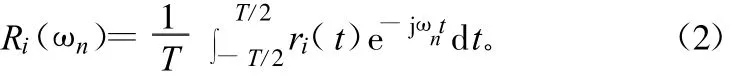
假設觀測時間遠大于信號掠過陣列的傳播時間,式(1)兩端用傅里葉系數表示后得到:

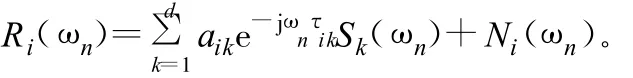
用矩陣表示即為:

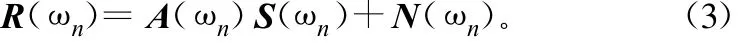
式中,R(ωn)和N(ωn)是m×1的矢量,

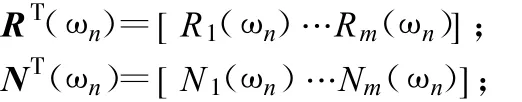
S(ωn)是d×1的矢量,ST(ωn)=[S1(ωn)…Sd(ωn)],并且A(ωn)是m×d的矩陣,

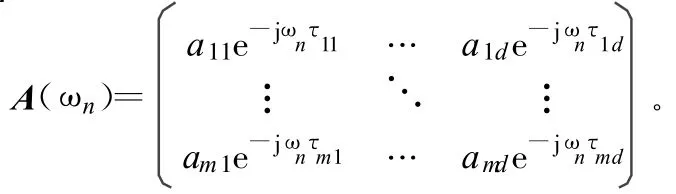
注意到A(ωn)的每一列與不同的信源相關聯,故可把列矢量表示為a(ωn,θk)(k=1,…,d),并稱為信源的方向矢量,假設A(ωn)滿秩。

將式(3)乘以它的轉置并求期望得到:

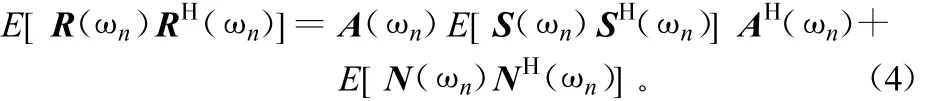
式中,H代表哈密特轉置。假設噪聲互不相關并且有相同的頻譜密度矩陣,可將式(4)改寫為:

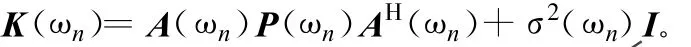
式中,K(ωn)和P(ωn)分別為過程和的頻譜密度矩陣;σ2(ωn)為噪聲的頻譜密度矩陣,并假設P(ωn)是非奇異的。

2 ISM算法

ISM算法是基于頻譜密度矩陣K(ωn)的特征分解的算法,它假設以下條件成立:

①信號的頻譜密度矩陣P(ωn)是非奇異的;

②任意d+1方向矢量是線性獨立的。

在這些條件下,K(ωn)的特征值 λ1(ωn)≤…≤λm(ωn)和特征矢量V1(ωn),…,Vm(ωn)有以下性質:

①K(ωn)的最小特征值為 σ2(ωn),并且重數為m-d,即

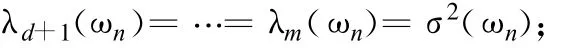
②最小特征值對應的特征矢量與列矢量是正交的,即

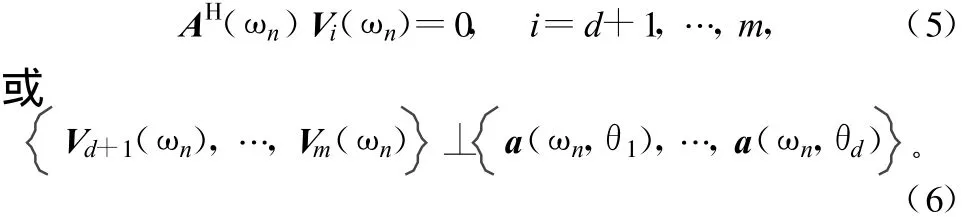
注意到式(5)或式(6)的正交關系對于帶寬B內的任意一個頻點ωn都成立。根據正交關系,信源數目可以由頻譜密度矩陣K(ωn)的最小特征值的重數來估計,K(ωn)的估計值為:

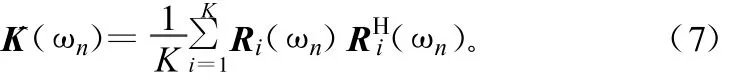
式中,Ri(ωn)為對應頻點 ωn處的第i個時域子間隔的傅里葉系數矢量;K為子間隔的數目。

用l1(ωn)≥l2(ωn)≥…≥lm(ωn)和C1(ωn),…,Cm(ωn)分別表示頻譜密度矩陣估計值的特征值和特征矢量,故其最大似然估計可表示為:

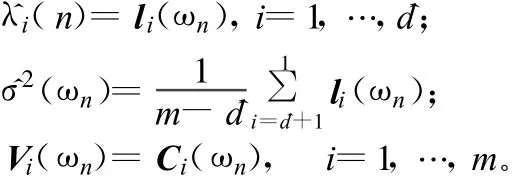
然后找到^d個最接近正交于矢量集{^V^d+1,…,^Vm}的θk,即為信源DOA。對各頻點和整個頻率范圍均使用算術平均可得到估計子:

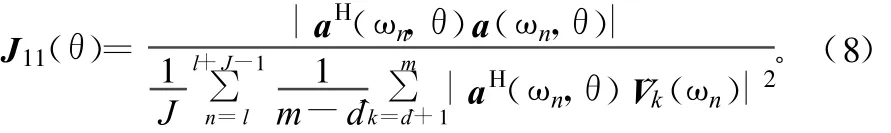
對各頻點使用算術平均而對整個頻率范圍使用幾何平均可得到估計子:

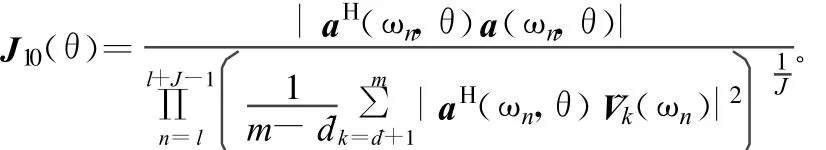
對于角度范圍進行搜索,找到^d個峰值對應的角度θ1,…,θ^d即為信源方位。

3 MISM算法

用Fs表示抽樣頻率,觀測時間T內的抽樣數目為:

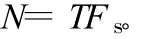
時間T內的抽樣稱為一次“快拍”,假設有K次快拍,整個抽樣時間即為T1=KT,于是式(2)變為:

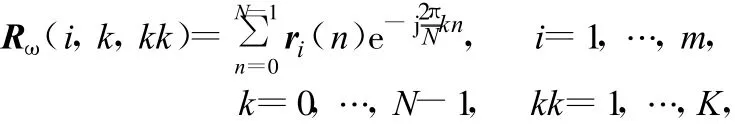
即為第i個傳感器在第k個頻點處的第kk次快拍,于是得到:

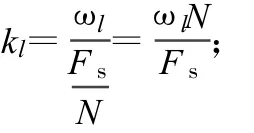
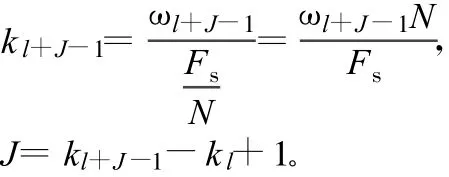
式中,J為帶寬B內的頻點數。為了說明MISM算法,定義頻點功率為:

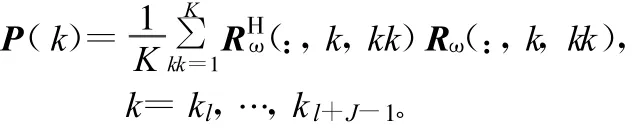
然后是找到最大功率對應的k值,即

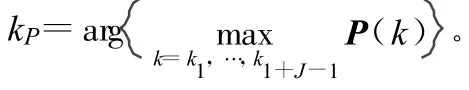
于是,式(7)和式(8)分別變為:

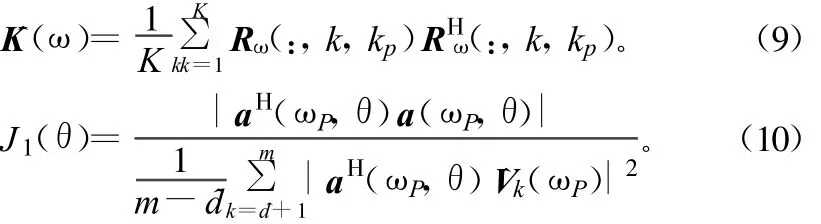
式(9)即用來計算特征值和特征矢量。可以看到MISM算法僅僅需要一次特征分解而ISM需要J次。

4 仿真實驗

陣列為均勻線陣,由16個各項同性的陣元組成,陣元間距為信號中心頻率的半波長。考慮2個帶寬相同的寬帶信源,中心頻率為100 Hz,相對帶寬為40%,抽樣頻率為240 Hz,假設信源方位角分別70°和75°。信號觀測時間為 26.67 s,應用式(10)的估計子,并且K=100,N=64。

4.1 分辨概率分析

根據上述仿真條件,信噪比為[-15∶15]dB,進行100次蒙特卡羅仿真得到2種方法的分辨概率如圖2所示。

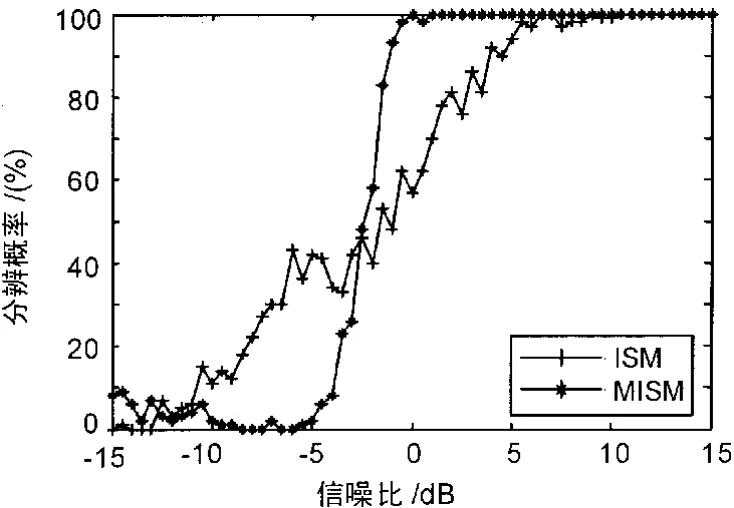
圖2 分辨概率

由圖2可知,從總體上看,在-2.5 dB以上,MISM算法的分辨概率大于ISM算法的分辨概率,在-2.5 dB以下,ISM算法分辨概率較高。ISM算法在10.5 dB達到100%的分辨率,而MISM算法在1 dB時即可達到100%分辨率,因此新算法所需的信噪比門限低。在實際應用中,信號在-2.5 dB以上很容易滿足,因此MISM算法具有實用價值。

4.2 誤差分析

假設信噪比為[-15∶15]dB,對2種算法的方差進行100次蒙特卡羅仿真得到方差圖如圖3所示。

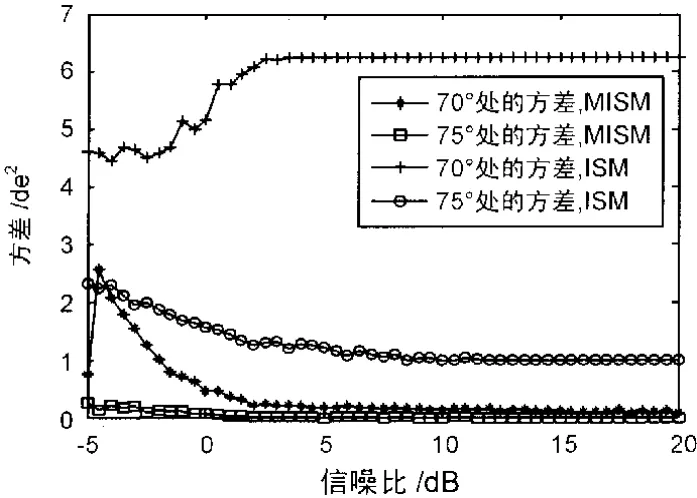
圖3 70°和75°的2種算法方差圖

由圖3可以看出,對于70°信源,MISM 算法比ISM算法方差要小4(degree×degree=de2)以上;對于75°信源,當信噪比大于1 dB時,MISM算法比ISM算法方差要小1(de2)左右,信噪比小于1 dB時,2種算法方差之差在減小,在-5 dB時差別還比較大,這是因為此時2種算法的分辨概率均較低,不能準確地分辨2個信源。

5 結束語

上述提出了一種基于最大功率進行頻點選擇改進的非相干信號子空間算法,不需要在每個頻點都進行窄帶信號測向算法,也不需要進行聚焦矩陣的計算,大大減小了算法運算量,提高了測向精度。對文中算法進行了仿真驗證,從仿真結果可以看出,新算法具有更低的信噪比門限和更低的測向誤差。可見文中算法具有一定的工程實用價值。

[1]謝 諾,葛建華,竇修全.基于ESPRIT寬帶信號測向技術研究[J].無線電工程,2009,39(12):17-19.

[2]WAX M,SHAN T,KAILATH T.Spatio-temporal Spectral Analysis by Eigenstructure Method [J].IEEE.TransactionASSP-32,1984(8):817-827.

[3]WANG H,KAVEH M.Coherent Signal-subspace Processing for the Detection and Estimation of Angles of Arrival of Multiple Wide-band Sources[J].IEEE.Transaction.ASSP-33,1985(8):823-831.

[4]VALAEE S,CABAL P.Wideband Array Processing Using a Two-sided Correlation Transformation[J].IEEE.Transaction.ASSP-43,1995(1):160-173.

[5]張賢達.現代信號處理[M].北京:清華大學出版社,2002.

[6]李石崗,叢玉良,張旭利.寬帶信號DOA估計的一種快速算法[J].吉林大學學報,2009,27(1):1-5.