無人機數據鏈信道線性Turbo均衡研究

甄云卉,邱金剛,陳自力

(1.河北省軍區,河北石家莊050011;2.軍械工程學院,河北石家莊050003)

0 引言

無人機遙控遙測系統在進行數據傳輸時,由于信道的多徑效應,信息在傳輸過程中常常會出現碼間干擾(ISI)的情況,這種干擾以及信道的平衰落、噪聲等其他干擾因素會嚴重影響無人機遙控遙測的質量。均衡技術就是為了降低或消除這些干擾因素,保證高質量通信的一種濾波方法。一般來說,信息序列經過信道編碼和調制之后,經過ISI信道送達接收端。在接收端,解調之后的信號通過串接的均衡器,調整均衡器參數,可以有效降低或消除信號失真,然后進行信道解碼,輸出正確的信息序列。

由于在傳統的均衡方式中,均衡器與解碼器是2個相對獨立的單元,解碼器對接收來的均衡器信息進行解碼,由于這種結構本身的特性,使得它對于均衡器判決后產生的突發錯誤無法很好地糾正,因而均衡的效果不太理想。

1 Turbo均衡原理

1993年,C.Berrou等人提出了一種性能優異的糾錯碼編碼——Turbo編碼。其中,Turbo碼的基于MAP準則的迭代解碼算法是Turbo碼取得良好性能的原因之一。分量解碼器之間可以相互利用對方輸出的軟判決信息,經過循環迭代,輸出解碼信息。

Turbo碼的基于MAP準則的迭代解碼算法中,分量解碼器之間相互利用對方輸出的軟判決信息,經過循環迭代,輸出解碼信息。由于迭代解碼的良好性能,可以設想把這種迭代方法應用到無人機數據鏈信道均衡中即Turbo均衡,提高無人機遙控遙測性能。研究表明,采用基于MAP的軟輸出均衡(SOE)算法可以使ISI信道達到接近加性高斯白噪聲(AWGN)信道的性能。無人機數據鏈信道Turbo均衡的結構如圖1所示。

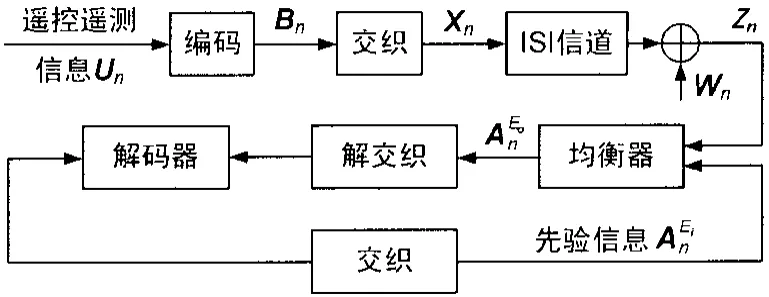
圖1 無人機數據鏈信道Turbo均衡器

初始均衡時,先驗信息=0,在以后的迭代均衡中,先驗信息和Y一起構成了均衡器的輸入。當均衡器輸出信息和解碼器的先驗信息趨于穩定后可達到最佳誤碼率,迭代均衡結束。Turbo均衡中,基于最大后驗概率的軟輸出均衡(MAP-SOE)算法的性能最優,但其最大的問題就是運算量較大,特別是在某些實時性要求較高的系統如無人機數據鏈系統中,其運算產生的延時往往會造成自身的誤差傳播。因此,在保證均衡性能的前提下,盡量降低運算量,減小系統處理延時是需要考慮的一個重要因素。這里設計使用線性均衡器(LE)來代替最大后驗概率均衡器。

線性均衡器有很多種,其中主要有:峰值失真準則均衡器、均方畸變準則均衡器和分數間隔均衡器等等。這里所采用的線性均衡器是最小均方誤差準則算法的線性均衡器(MMSE-LE)。

2 基于MMSE的線性均衡算法

這里采用的基于MMSE線性均衡器結構如圖2所示。其中包括MMSE準則估計器以及一個將碼元估計值映射為概率信息的映射函數部分構成。

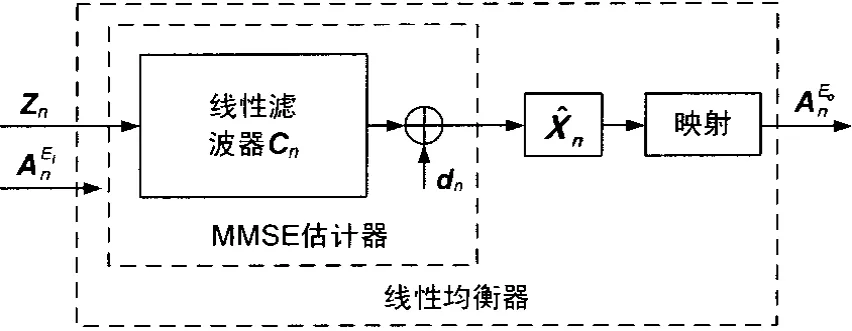
圖2 MMSE線性均衡器

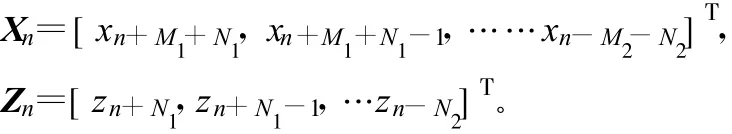
Zn與Xn的關系為:

式中,Wn是均值為0、方差為的高斯白噪聲序列;H為無記憶離散信道的卷積矩陣,

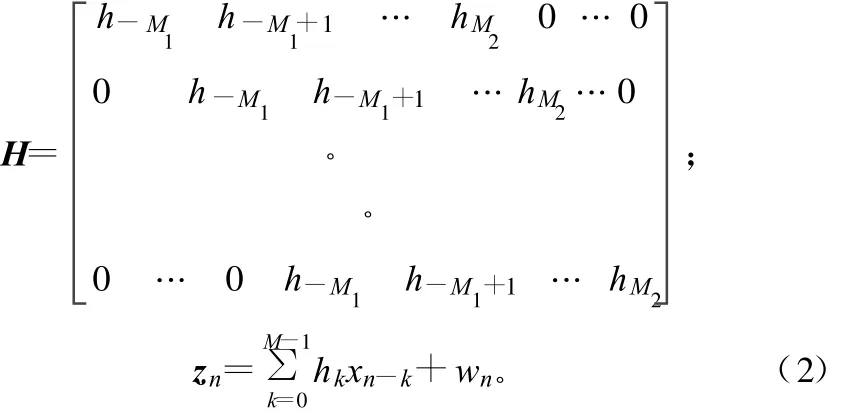
序列Zn經過估計器之后,輸出的Xn估計值為:

在MMSE-LE中,Cn和dn是2個重要的時變參數,其中Cn為均衡器的抽頭系數,dn為一個時變的偏差修正參數,是為了修正由反饋信息引起的變量Xn的均值變化。在每次迭代時都要對Cn和dn進行求解。求解是通過估計誤差的均方值E最小化來確定的。

設均衡器的抽頭有N=N1+N2+1個,抽頭系數Cn=[c-N…c-N]T,偏差修正參數dn,則

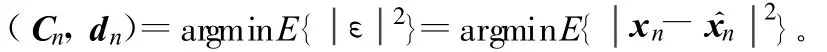
通過偏導數來求函數的極值點,分別對Cn和dn求偏導數并令其為零:

將式(5)和式(6)代入式(3)就可以解得xn的估計值為:

這樣,均衡器就可以利用解碼器反饋信息以及接收到的信息Zn通過式(5)、式(6)、式(9)、式(10)～式(12)等式來計算^xn。第1次迭代時,均衡器接收的先驗信息

3 仿真實驗

以下通過計算機仿真實驗驗證Turbo均衡在無人機數據鏈信道中的性能。信道編碼是碼率R=0.5的系統遞歸卷積碼,生成多項式G(D)=[7,5],所用模擬無人機數據鏈信道的是具有嚴重ISI的Proakis'B信道,沖激響應為h(t)=0.815(t)+0.407(t-1)+0.407(t+1),信道噪聲是方差為σ2,均值為0的高斯噪聲,交織器采用偽隨機交織器,交織長度為2 048。圖3給出了采用MMSE線性均衡器的Turbo均衡的誤比特率(BER)性能曲線,為了便于比較,同時還畫出了無ISI信道的誤比特性能、普通經典線性均衡(LE)方法以及采用MAP算法的Turbo均衡的性能曲線。

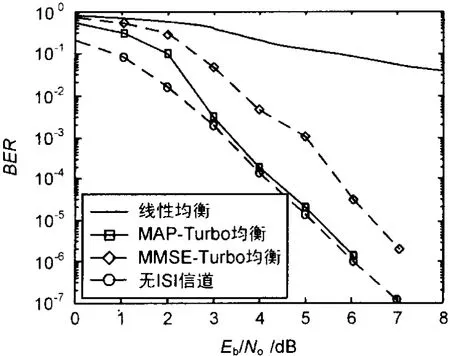
圖3 不同均衡算法性能比較

從圖3可以看出,使用MAP算法和使用MMSE線性均衡器的Turbo均衡的性能要明顯優于經典的線性均衡方法,在低信噪比(Eb/No＜2 dB)時,3種均衡的性能約在同一個數量級上,當信噪比增大時,使用MAP算法和使用MMSE線性均衡器的Turbo均衡的BER迅速下降,顯示了Turbo均衡性能的優越性。同時,在中高信噪比(Eb/No＞3 dB)的情況下,可以明顯看出在信噪比相同的條件下,使用MAP算法的Turbo均衡比使用MMSE線性均衡器的Turbo均衡的性能基本高出一個數量級,這是MAP算法與MMSE線性均衡算法性能所決定的。但同時在試驗中使用MAP算法的Turbo均衡的運算量和運算時間遠大于使用MMSE線性均衡器的Turbo均衡。圖4給出了不同迭代次數對于MMSE線性Turbo均衡的性能影響。

圖4 不同迭代次數對MMSE線性Turbo均衡性能影響

結果表明,迭代次數對均衡性能有比較明顯的影響,當迭代次數小于4次時,均衡的性能改善明顯,隨著迭代次數增加(10次以上),迭代產生的增益不明顯,其BER的值基本上在同一數量級上小幅變化,在信噪比較大(5 dB以上)時,經過4～5次迭代,其均衡性能就已比較接近MMSE線性Turbo均衡的最優性能。

4 結束語

比較MAP算法Turbo均衡性能和使用MMSE線性均衡器的Turbo均衡性能,前者的最優性能較后者最優性能雖高出一個數量級,但其運算量較大,系統處理延時時間較長,在該仿真實驗中相同的信噪比條件下(Eb/No=7 dB),以容許的BER=10-6為標準,使用MAP算法的Turbo均衡迭代3次滿足要求,使用MMSE線性均衡器的Turbo均衡迭代4次滿足要求,但從系統處理時間及延時來看,雖然前者迭代次數較少,但運算量大,處理時間相比后者多出約100～200 ms。因此綜合考慮性能及實時性要求,使用MMSE線性均衡器的Turbo均衡方法能夠滿足無人機數據鏈信道的均衡要求。

[1]PROAKIS JG.數字通信[M].張力軍,譯.北京:電子工業出版社,2003:444-470.

[2]曹志剛,錢亞生.現代通信原理[M].北京:清華大學出版社,1992.

[3]TUCHLER M,KOETTER R,SINGER A.Turbo Equalization:Principles and New Results[J].IEEE Transactionson Communications,2002,50(5):754-767.

[4]TUCHLER M.IterativeEqualization UsingPriors[M].University of Illinois,2000.

[5]韓 琮,郭淑霞,陳志坤.無線通信中Turbo均衡技術及應用[J].計算機工程與應用,2008,44(30):105-107.