多領域相互滲透的高等數學教學模式

李欣越 趙秋蘭 王 麗

（1.山東科技大學理學院 山東 青島 266510；2.山東德州一中 山東 德州 253000）

0 引言

工科院校高等數學[1]教學，一直就是各個學校發展的生命線。在教學方法與教學手段日益發展的今天，在人才需求與各項體制改革高度密集的當今社會，高校教師正日復一日的在進行著教學不斷改革。隨著科學技術及社會的不斷發展,數學的應用無疑會更加廣泛,所賦數學的功能和價值也會隨之擴大,因而高校對數學教育需重新審視和把握.顯然,這對數學教育也提出了新的要求,而現有的教學模式根本無法滿足這種要求.因為傳統模式倚重于知識傳承,把傳承性教學置于中心位置,忽視學生自主學習、自主探究能力的培養,培養出的人才大多欠缺創新思維、想象力和創新能力。

伴隨工科數學教學改革的深人,由傳統的傳授知識為主體的知識教育轉向以培養能力為主的素質教育是必然的趨勢。以知識為載體,在傳授知識的同時,更加注重能力的培育和素質的提高,這正是素質教育的基本思想。如“立體化的教學模式”在工科數學中的改革[2]、數學實驗[3]與數學建模[4]數學教學的結合等等。

為了把工科數學這條生命線抓住，很多高校把數學實驗與數學建模分別作為獨立課程開設起來。這樣固然出發點是好的，但這樣就割裂了傳統數學課程與數學實驗、數學建模之間的關系,忽視了數學實驗、數學建模理念在工科數學中真正的價值。同時還要注意各門數學課程之間的有機聯系與滲透、所開設數學課程的相關專業也得有機結合，這樣學生才能真正把自己投入到數學的自主學習中去。

1 高等數學課程知識點之間的滲透與提煉

本著以形成融傳授知識和培養能力為一體的教學模式，深化以創新意識和實踐能力培養為核心的教育理念，構建以技術應用為主線、多學科滲透的立體式教學體系的指導思想，進行藥理學教學研究。將德育教育、人文社科知識及醫學相關知識滲透到教學中，激發學生涉獵知識的興趣，教會自主學習的方法，培養終身學習的意識，提高綜合素質，增強社會適應性。

眾所周知，高等數學的特點是知識點多而雜，表現在定義定理多、運算公式多、應用技巧強、知識點間邏輯關系密切等。我們很清楚，平時在做題應用時發現不少知識點與方法在課本中并沒有提到。那是肯定的，知識無時無刻不在更新，簡單的一本教材怎么可能把相關的所有知識點都包含其中呢？這就要求我們在學習當中盡可能地把書本上的知識深入理解，多比較、多聯想，這才可能真正把書本知識用活。

舉例說明：高數（同濟六版）下冊總習題十一有一道題：

分析：該題目并不難，市面上那些琳瑯滿目的習題解答幾乎都是用直系定限來完成的。實際上我們如果吃透了柱面坐標系，該題用柱系定限顯得更為簡單。實際上下面三種形式

都是柱面坐標系，教材上給的是第一種形式的柱系，而該題我們用第二種形式。

點評：只要被積函數為形如：x2＋y2，y2＋z2，x2＋z2三種形式用柱系定限都很簡潔。

又如三重積分中的“先二后一”方法在教材中有一個實例已經討論過，試問如果把該題的被積函數改為關于x的表達式或關于y的表達式而積分區域不變，該題還能用此法嗎？實際上回答是顯然的，只不過要用x＝t或y＝t不同的平面來截橢球面而已。

2 數學實驗在高等數學教學中的滲透

隨著計算機技術的迅速發展,以前單純的“黑板+粉筆”的原始模式已經遠遠不能滿足當前的數學教育需要了，這也引導了教育教學的地位。同時數學學科也在不斷滲透到其他所有的課程之中。數學實驗是培養學生解決實際問題和創新能力的一個非常重要的途徑,已成為我國當前工科數學教學改革的一個熱點。

數學實驗與傳統實驗教學存在很大的區別，那就是數學實驗是信息時代的產物，它是計算機技術介入數學教學與數學研究的必然結果。數學實驗就是以計算機為工具，運用Matlab、Mathematica、Maple等數學軟件加工各種數學信息。它可以說是對人類思維過程的一種模擬與驗證，而不像物理、化學實驗那樣是對自然現象的一種模擬與驗證。另外，數學實驗課與傳統的數學課程也有很大區別，數學課主要是講相應課程的數學理論,注重知識的傳授與邏輯推理能力的培養，而數學實驗課是用實驗的方法來驗證數學理論，以及應用數學理論來解決實際問題，數學實驗課有助于學生更好地學習數學理論課。

開設數學實驗課是數學教學的一種新的嘗試，它的教學內容、教學方法、教學手段都值得我們深人地研究和探索。它最重要的一點是開放式的教學環境，其課程開設的思路和作法應各種各樣，只求目的，不拘泥于模式，鼓勵各種不同的想法和作法，鼓勵百花齊放，各自進行自己的探索和試點。

我認為創新實驗教學理念，提高學生能力，鼓勵學生利用所學理論和現有的實驗設備，合理進行實驗技術和方法的革新。打破常規實驗教學模式，培養和鍛煉了學生的創新精神和意識，提高了學習的興趣，達到了工學結合的目的。特別是在高等數學這樣一門及其重要的基礎課而言，不僅僅是讓學生懂課本知識，更重要的是通過數學實驗課讓學生具備動手能力，學會運用計算機這個必備工具更簡潔高效地去解決問題。

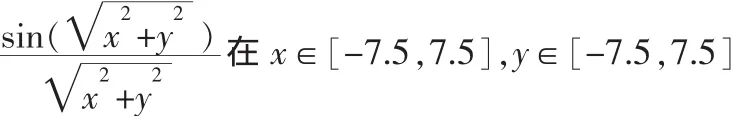
我們應用Matlab編如下程序就能輕松解決：

3 數學建模在高等數學教學中的滲透

什么是數學建模（mathematical modelling），簡單的說就是通過合理的假設、收集大量有用數據，運用所學的數學知識，建立反映與解決實際問題的數量關系的一種數學實踐活動。數學建模并不是在近幾年提出的新名詞，可以說數學建模是伴隨著數學的發展始終。為什么這么說呢？在高等數學中，經常有解決實際生活中的用料最省、體積最大以及經濟理論中的最大利潤、最小成本、邊際、彈性分析等問題。定積分中的微元法也是應用中的有效方法，可以用來計算面積、旋轉體的體積、圖形的重心等。

在教學過程中適時融入數學建模思想，對各專業特別是經濟管理類專業的學生更有助于專業課的學習、抽象思維的提高，使得學習經濟學和管理學變得容易，而且可以更完整、更深刻地理解和解釋各個工科專業中的某些理論。如2006年的數學建模題是關于易拉罐的形狀設計問題，這顯然是數學中一定的條件下的單一目標優化問題；2007年的乘公交看奧運問題就是一個多目標優化問題；2008年的數碼相機定位問題是運用物理中的公切線成像原理的數學模型。當然這些題目的順利解答不是單純的用某一方面的數學知識。因為數學建模具有這樣的特點：高度的抽象、概括性、知識與能力的綜合性、應用的廣泛性、問題的時效性。

最近幾年，各個高校、專業的學生都紛紛加入到數學建模的隊伍中來。數學建模旨在培養大學生分析、綜合和解決實際問題能力、有助于提高大學生的創造能力與相互協調能力、有助于大力增強學生的自學能力、有助于培養學生關心國家大事增強愛國情感的能力。

隨著社會的高度發展與科技的日益進步，對學生能力的要求日益迫切，這也就對高等數學這樣重要的基礎課教學教育提出了更高的要求。在高等數學教學中貫徹數學實驗與數學建模的思想是新時代的要求。

［1］同濟大學.高等數學[M].同濟大學高等數學高等教育出版社.

［2］于慶年.高等數學課程“立體化”教學模式的思考[J].遼寧師專學報,2008(9)：3-6.

［3］謝云蓀，張志讓.數學實驗[M].北京：科學出版社，1998.

［4］李大潛.中國大學生數學建模競賽[M].北京:高等教育出版社，2008.