空間目標成像原理及運動控制

陳乾輝，王小芬

（1.商丘科技職業學院 機電工程系，河南 商丘 476000；2.商丘科技職業學院 計算機科學系，河南 商丘 476000）

0 引 言

近年來，隨著計算機視覺技術的飛速發展，在目標追蹤、定位、識別及智能控制方面有了廣泛應用。它從攝像機獲取的圖像信息出發，計算三維空間中物體的幾何信息，而空間物體表面某點的三維幾何位置與其在圖像中對應點之間的相互關系是由攝像機成像的幾何模型決定，因而完成映射到單幅或多幅圖像上的三維場景，如三維場景的重建。

運動目標的序列圖像跟蹤要用一種算法來實現，然而由于其軌跡的不確定性，因此可以通過攝像機的運動控制來實現，即可以通過攝像機的左右平移和俯仰旋轉，獲取物體的三維姿態信息進行三維建模，得到目標的模擬軌跡。

1 攝像機標定

為獲得攝像機的內部參數，在大多數條件下這些參數必須通過實驗與計算才能得到，這個過程被稱為是攝像機定標。攝像機的內部參數指攝像機成像的基本參數，如主點，攝像機的外部參數指攝像機相對于外部世界坐標系的方位，而攝像機標定目的就是獲取某些內外參數。計算機視覺中幾何模型參數就是攝像機參數。

現有的攝像機定標技術大體可以歸結為兩類：傳統的攝像機定標方法和攝像機自定標方法。

傳統攝像機定標方法有4類：

1）利用最優化算法的定標方法；

2）利用攝像機變換矩陣的定標方法；

3）進一步考慮畸變補償的兩步法；

4）采用更為合理的攝像機成像模型的雙平面定標方法。

攝像機自定標方法有4類：

1）利用本質矩陣和基本矩陣的攝像機定標方法；

2）利用絕對二次曲線和外極線變換性質的攝像機定標方法；

3）利用主動系統控制攝像機做特定運動的自定標方法；

4）利用多幅圖像之間的直線對應關系的攝像機定標方法。

總之，攝像機標定在從計算機圖像坐標中導出三維幾何信息以及由三維信息導出二維計算機圖像坐標的應用中起著重要作用。

2 攝像機成像原理

攝像機成像模型包括常用投影和針孔成像模型。常用投影又分為中心投影和平行投影，即投影射線匯聚于一點的投影稱為中心投影，投影射線相互平行的投影稱為平行投影。而對于三維空間物體到像平面的投影關系稱為成像模型，其中理想投影成像模型則稱針孔模型。

2.1 成像模型

在空間目標成像模型中，為確切掌握空間目標的姿態信息，必須將其坐標轉換到同一坐標系下。因此定義了3個坐標系：O－XYZ 坐標系是世界坐標系，乃用戶定義坐標系，表示場景點的絕對坐標。OC－XCYCZC是攝像機坐標系，其中，OC為攝像機光心，ZC軸與攝像機的光軸重合，取攝影方向為正向。O′xy是圖像坐標系，表示場景點在圖像平面上的投影。XC軸、YC軸分別與X 軸、Y軸平行，ZC是攝像機的光軸，它與圖像平面垂直。三坐標系之間的轉換關系見表1。

表1 坐標轉換

物點、光心和像點三點共線，且fx，fy，u0，v0為攝像機內部參數，r11，r22，…，r33是正交旋轉矩陣的系數。

取f為攝像機焦距，光軸與圖像平面交點，O′為圖像坐標系的原點，選取飛行器的某點P（X，Y，Z）作為目標點，在圖像平面上的投影點為p（x，y），成像幾何模型如圖1所示。

圖1 成像幾何模型

在不考慮攝像機鏡頭畸變的情況下，可得透視投影成像模型（其中：（x，y）為像點坐標，（XS，YS，ZS）為攝影中心坐標，a1，a2，a3，b1，b2，b3，c1，c2，c3為坐標變換中矩陣元素，且當變換關系一定時，變換矩陣元素已知）為：

2.2 極線約束

根據外極線幾何理論，三維空間一點在兩個像平面上的投影點稱為對應點對，且對應點對中的一點位于另一個點所確定的外極線上，如圖2所示。

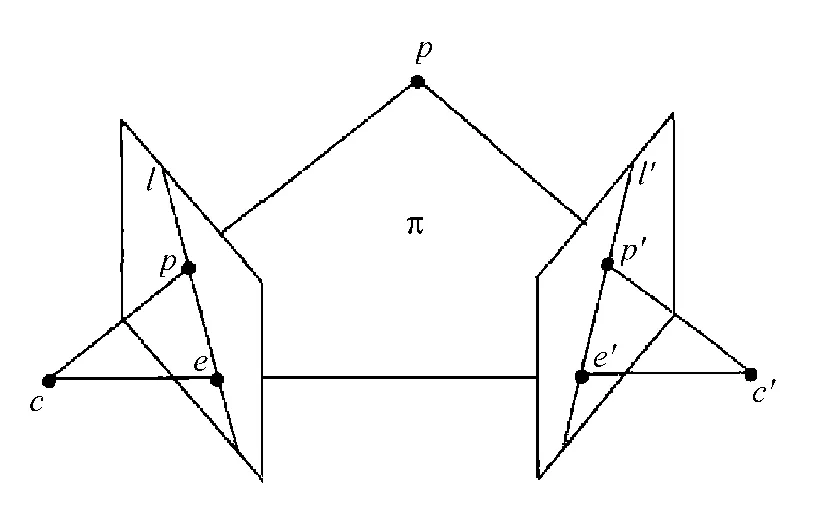
圖2 極線幾何約束關系

假定以經緯儀C為測量坐標系的基坐標系，得關系式

3 攝像機運動控制及算法實現

為獲得序列圖像以掌握空間目標運動，必須了解圖像的運動軌跡。攝像機一般固定在光電設備上，由于光電設備圍繞地球坐標軸左右擺動和上下俯仰，其坐標變換相當復雜，不適宜平移運動，若旋轉是圍繞以圖像平面為中心的系統，則推導就相對簡單。因此，根據所作用的信號，這里采用光電設備的左右平移運動或使用攝像機的上下俯仰運動，以獲取圖像信息。

3.1 圖像平面位置變化的影像

跟蹤系統的結構和數字模型如圖3所示。

圖3 跟蹤系統模型

該系統由光電設備上的攝像機、圖像處理系統和控制光電設備的計算機接口3大部分組成。所需要建立的模型是描述原始圖像坐標（）和經過擺動和俯仰運動的圖像點坐標之間的關系。

坐標變換依賴于攝像機焦距f，左右擺動角φ、俯仰角θ和地球坐標系原點與圖像平面坐標原點偏移量（Tx，Ty，Tz）、原始物體點（x，y，z）與圖像點（xi，yi）之間的差，以及經過左右和俯仰運動的物體點（x′，y′，z′）與圖像點（）之間的差值，坐標變換見表2。

表2 擺動和旋轉坐標變換

表3 圖像平面（物理）之間坐標關系

3.2 攝像機運動的控制算法

為得到偏差矢量T＝（Tx，Ty，Tz）的精確值，我們對變換公式進行了研究，發現當伸縮比很大時，可以忽略該偏差影響。并由可以用逼近，忽略上述方程中的。當很大時，得圖像平面（物理）之間坐標關系及三維姿態角（見表3）。

4 結 語

通過攝像機成像原理以及空間目標三維轉換模型的分析，使我們了解坐標變換的重要作用，并由攝像機運動控制及算法的實現算出了空間目標三維姿態角，此研究對目標特性視覺化具有重要的理論和現實意義。

［1］王巧華，文友先，劉儉英.我國機器視覺技術的發展前沿［J］.農機化研究，2000，11（4）：16－18.

［2］張祖勛，張劍清.數字攝影測量學［M］.武漢：武漢大學出版社，1997：1－6.

［3］Armin Gruen.Digital photogrammetric stations re－visited［J］.Int.Arch.Of Photo－grammetry and Remote Sensing，1996，31（B／2）：127－134.

［4］張祖勛.數字攝影測量的發展與展望［J］.地理信息世界，2004，2（3）：1－5.

［5］張祖勛，張劍清.數字攝影測量在我國的發展與應用［EB／OL］.（2010－04－25）［2011－08－20］.http：／／wenku.baidu.com／view／18a75f649b6648d7c1c74672.html.

［6］張祖勛.數字攝影測量與計算機視覺［J］.武漢大學學報：信息科學版，2004，29（12）：1035－1039.

［7］袁野.攝像機標定方法及邊緣檢測和輪廓跟蹤算法研究［D］：［博士學位論文］.大連：大連理工大學，2002.

［8］王之卓.攝影測量原理［M］.武漢：武漢大學出版社，2007.