基于自適應模糊的印刷色彩質量控制及Simulink仿真

康建山，初紅艷，楊俊敬

（北京工業大學 機電學院，北京 100124）

0 引言

隨著智能控制的不斷發展，模糊控制以其無需建立系統數學模型、對參數變化不敏感、與其他控制方法具有很強的融合性等特點被大量應用于實際的生產管理控制當中。如模糊PID控制、模糊神經網絡控制、模糊自適應控制等在應用中都取得了顯著的控制效果[1]。

由于印刷機印刷過程的傳遞函數難求、檢測數據少且要求調整快速等特點，同時這類大滯后非實時系統的工藝條件受工作環境影響而容易出現色彩質量偏差等問題。傳統控制方法多是基于人工調整，受人為因素影響。本文提出了基于自適應模糊控制方案，利用墨鍵—密度控制曲線得到其控制規則，并根據生產過程中的檢測數據對控制規則系數進行修正，較快地提高了控制精度，減少調整次數。

1 問題描述及解決方案

印刷品的色彩質量可由其實地密度體現，而其主要的影響因素是給墨量的多少。現代生產中主要通過控制步進電機調整墨鍵開度以控制給墨量。目前多數中高檔印刷機都配置了油墨預置功能，該預置數據主要由實驗數據得到，但是受到實驗條件的約束，實際生產過程中，需要人工修正墨鍵開度大小以調整色彩質量。

由于印刷機的印刷過程需要一定的穩定時間，同時印刷機色彩質量檢測屬于離線檢測且要求快速調整達到期望，因此常規調整很難達到規定要求，需要考慮新的色彩質量控制方法。

1.1 墨鍵—密度控制曲線

墨鍵—密度曲線表示在某特定工作條件和網點面積率條件下，不同墨鍵開度與其對應的印刷品實地密度關系曲線。雖然影響印刷質量的因素除了給墨量，還有其工藝因素如溫度、印刷壓力、速度以及油墨粘度等[2]，但是由于印刷過程的連續性，其生產工藝影響在一定范圍內，所以墨鍵—密度控制曲線的總體趨勢保持不變。

實際生產中應用的曲線在要求的精度范圍內大都能用二次曲線來擬合。設期望實地密度為R，將墨鍵—密度控制曲線表示為

將墨鍵—密度控制曲線在初始墨鍵開度xo處泰勒展開得到

式中：xo—當前墨鍵開度；

f(xo)—墨鍵xo對應的實地密度值；

xs—調整后得到的墨鍵開度；

f(xs)—墨鍵開度xs時對應的實地密度；

f '(xo)—墨鍵xo處的斜率。

因此可以利用墨鍵—密度曲線來取得期望實地密度下的墨鍵開度值，并通過對控制曲線一定規律的調整以適應工藝條件的變化，并實現色彩質量的控制。

1.2 自適應模糊控制方案

由于模糊控制更接近人的思維方法和推理習慣，因而適用于非線性、大滯后的印刷過程控制中。而且通過其控制規則的自適應調整，使得控制規則對工藝條件的適應性更強。

一般自適應模糊控制器的控制框圖如圖1所示。

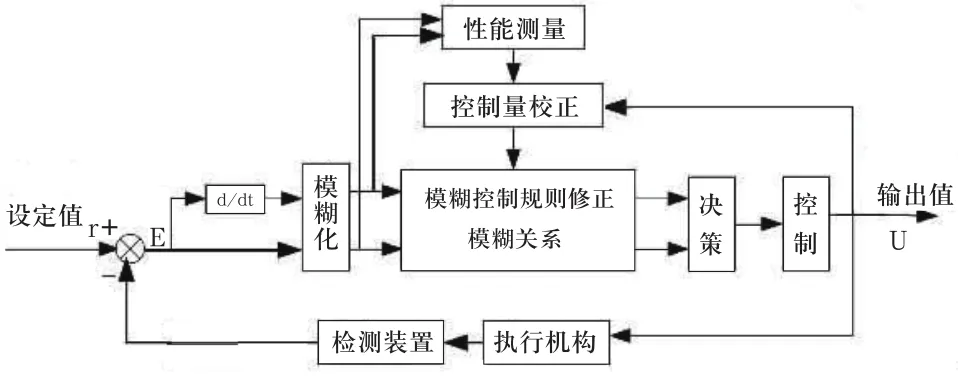
圖1 自適應模糊控制框圖

自適應模糊控制器在簡單模糊控制器的基礎上增加了三個功能塊，即性能測量、控制量校正和控制規則修正，其中性能測量用以衡量設定值的偏離情況；控制量校正部分將設定值所需要的校正量轉換為對控制量的校正量；控制規則校正根據控制量校正所得到的校正量修正控制規則表中控制量，使控制規則更加合理，使系統的輸出朝期望的方向變化[3]。

因此，根據式（2）可以方便的得到基于T-S模型的控制規則。同時，利用控制器的自適應功能，可以調整控制規則以適應生產條件的變化，達到期望的控制效果。

2 模糊控制器設計

根據對問題的描述，設計墨鍵控制自適應模糊控制器控制圖如圖2所示。

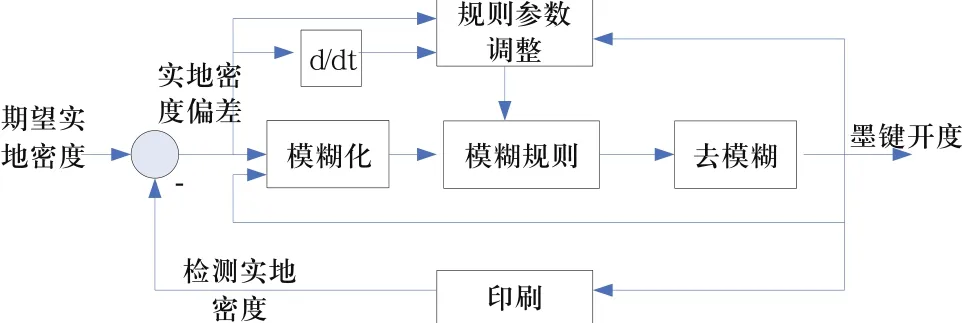
圖2 墨鍵控制自適應模糊控制框圖

通過對印刷品實地密度的檢測，利用其與期望實地密度的偏差和當前的墨鍵開度作為模糊控制器的輸入，得到調整后的墨鍵開度，同時根據實地密度偏差及其變化對控制器控制規則進行調整。

2.1 隸屬度函數及去模糊方法的選擇

根據經驗確定實地密度偏差的論域為[-0.5 0.5]，墨鍵開度的論域為[0 70]。采用三角形隸屬度函數，實地密度偏差和墨鍵開度的隸屬度函數分別如圖3和圖4所示。

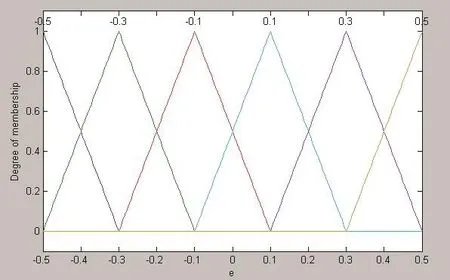
圖3 實地密度偏差的隸屬度函數

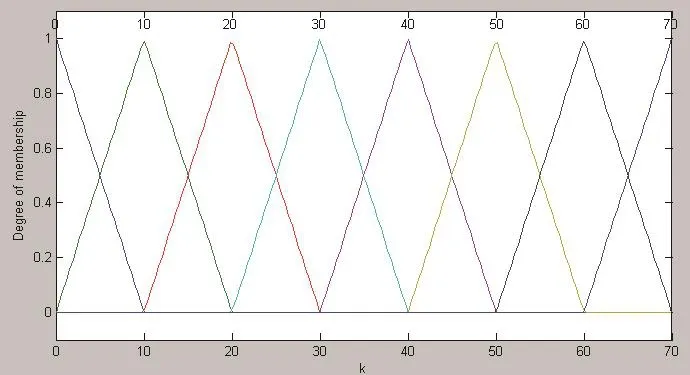
圖4 輸入墨鍵開度的隸屬度函數

采用重心法作為去模糊方法，模糊系統的輸出量為每條規則的輸出量的加權平均[4]：

2.2 控制規則的確定

根據一般經驗總結，當實地密度偏差大時，墨鍵開度的調整也應隨著大些，反之調整量小；同時，在同樣實地密度偏差情況下，墨鍵開度調整量又與當前墨鍵開度有關；當實地密度偏差小于允許偏差時墨鍵開度不需要調整。

T-S模型能夠方便地進行非線性系統建模和設計，其第j條控制規則可描述如下：

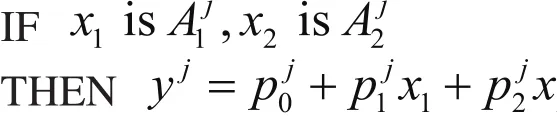
其中x1，x2為輸入變量，在印刷機色彩質量控制中為實地密度偏差和墨鍵開度值，A1，A2分別為兩個輸入變量的模糊語言值。

由公式(2)易知，控制規則中p0=0，p2=1，p1=1/f'(x)，系數p1的取值可根據輸入墨鍵開度值確定，因此需要根據墨鍵—密度控制曲線確定控制規則系數p1的參數表，并由此參數表選擇特定條件下的系數值。

2.3 控制規則參數表的調整

為適應工藝條件的變化，控制規則參數表需要根據檢測實地密度偏差作出相應調整。設墨鍵開度初始值為xo，墨鍵開度為xt時對應期望實地密度R。第一次檢測得到實地密度偏差為eo，如果未達到要求，需要對墨鍵開度進行eo/f'(xo)的調整，調整后墨鍵開度為xs，再次印刷后檢測到的實地密度偏差e1。如果偏差仍未達到要求，則需要第二次墨鍵調整，同時也說明受各種影響因素的影響，實際的墨鍵—密度曲線發生變化，斜率需要進行校正，而控制規則參數p1包含了斜率的所有信息，因此只需要對p1進行調整。

設ft'(xo)表示xo處斜率調整后的斜率值。調整方法如下：

由公式(2)得

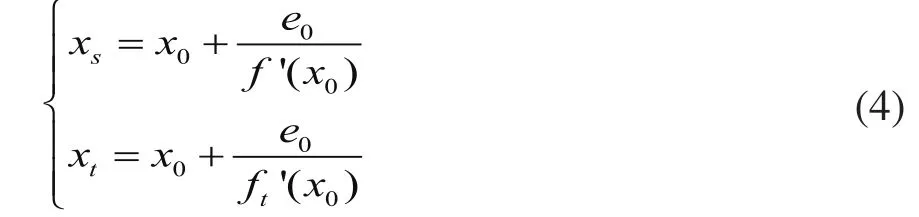
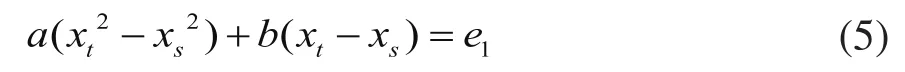
將公式（4）代入公式（5）可近似得

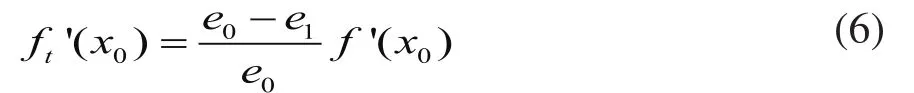
3 仿真

以印刷機的墨鍵控制為例，利用matlab對控制算法進行仿真驗證。通過實驗得到某印刷機在某工藝條件下網點面積率為50%的墨鍵—密度數據表如表1所示。

表1 網點面積率50時墨鍵—密度表

通過對實驗數據進行二次曲線擬合得到的墨鍵—密度控制曲線為

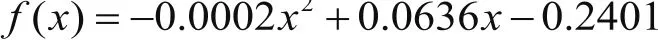
根據控制曲線得到網點面積率50%的控制規則參數表，即系數p1的參數表，如表2所示。如果將其他網點的控制規則參數表也添加到表2中，就可以得到總的控制規則參數表。

表2 網點面積率50的控制規則參數表

利用Matlab中的Simulink模塊構建仿真框圖如5所示

圖5 印刷機墨鍵自適應模糊控制框圖

其中：respect模塊指定期望實地密度值，這里設為1.5；fadapt模塊為S-Function[5]，其中包含了控制規則參數表，以及相應的自適應模糊控制算法；condition模塊是現場的生產加工曲線，即實際的輸入輸出關系，假設為

墨鍵開度的初始值根據以往實驗結果設置為30，控制規則參數表如表2所示。下面進行三種仿真。

3.1 利用原始控制規則參數表進行墨鍵控制

第一次檢測實地密度偏差為0.413，利用原始規則參數表2對墨鍵開度進行調整后，得到墨鍵開度為38，印刷后檢測得到實地密度偏差為0.1074。再次利用原始參數表調整得到墨鍵開度40，印刷后實地密度偏差0.0352，達到允許偏差，其實地密度調整效果如圖6所示。

3.2 利用本文的控制規則參數自適應調整算法進行墨鍵控制

由于墨鍵開度初始值為30，印刷后檢測得實地密度偏差為0.413，利用原始參數表2，進行第一次墨鍵開度調整，得到墨鍵開度為38，印刷后檢測得到實地密度偏差為0.1073，未達到期望范圍，得知控制規則參數未能很好地反應實際情況。利用調整算法進行規則參數調整后，再對墨鍵開度進行調整得到41，檢測得到實地密度偏差為0.006，密度調整效果如圖7所示。控制規則參數表調整如表3所示。

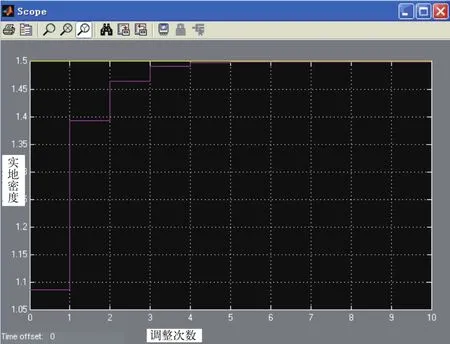
圖6 控制規則參數不調整的密度調整效果

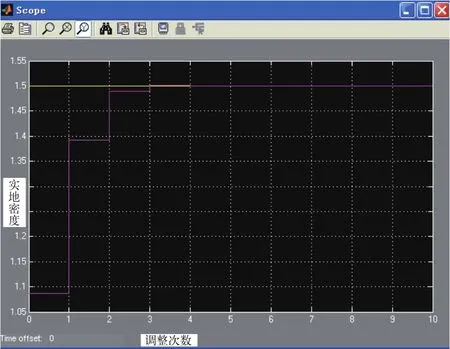
圖7 參數自適應調整算法的密度調整效果

表3 網點面積率50的調整后規則參數表

3.3 利用調整后的規則參數表進行墨鍵控制

將調整后的參數表3作為原始規則參數表。首次檢測得到實地密度偏差為0.413，經過一次墨鍵調整便得到41，實地密度偏差為0.006，符合規定要求，不需參數表調整，得到的實地密度調整效果如圖8所示。

圖8 利用調整后規則參數的調整效果

通過以上三種仿真，可以看出方法2要優于1，而且方法3經一次調整就能達到要求。說明通過對控制規則參數的調整，能較快的達到控制效果，而且其調整結果較符合實際情況。

4 結束語

針對印刷機的印刷過程具有非實時、大滯后且檢測數據少的特點，分析其控制輸出不能很好地跟蹤實際生產條件的問題，提出了利用自適應模糊控制的方法，通過對控制規則參數的調整達到調整控制曲線進而實現色彩調整的目的。利用matlab對膠印機墨鍵控制進行仿真，驗證該方法在控制曲線趨勢不變條件下收斂穩定，且調整速度快；并且在實際應用中，該算法運算簡單，易于實現。

[1] 文生平,趙國平.一種變論域模糊控制自適應算法[J].控制理論與應用,2009,26(3):265-268.

[2] 劉世昌.印刷品質量檢測與控制[M].印刷工業出版社,2000.[3] 章衛國,楊向忠.模糊控制理論與應用[M].西北工業大學出版社,2000.

[4] 張豪.基于單片機的模糊控制在節水灌溉控制系統中的實現[D].江南大學,2007:17-25.

[5] 費春國.模糊自調整控制器的研究及應用[D].天津科技大學,2003:19-28.