內(nèi)蒙古“金三角”地區(qū)能源消費(fèi)與經(jīng)濟(jì)增長(zhǎng)關(guān)系研究——基于面板數(shù)據(jù)的協(xié)整分析
孟 軍
(1.內(nèi)蒙古財(cái)經(jīng)學(xué)院 統(tǒng)計(jì)與數(shù)學(xué)學(xué)院,內(nèi)蒙古 呼和浩特 010051;2.東北財(cái)經(jīng)大學(xué),遼寧 大連 116025)
引言
內(nèi)蒙古是我國(guó)北方重要的能源大省,尤其是地處內(nèi)蒙古“金三角”地區(qū)的呼和浩特市、包頭市、鄂爾多斯市,簡(jiǎn)稱“呼包鄂”,以其突出的能源優(yōu)勢(shì)為內(nèi)蒙古經(jīng)濟(jì)社會(huì)的快速發(fā)展做出了重要貢獻(xiàn),經(jīng)濟(jì)實(shí)力雄踞自治區(qū)之首。與此同時(shí),經(jīng)濟(jì)社會(huì)的發(fā)展越來(lái)越受到資源環(huán)境的約束,環(huán)境問(wèn)題、能源與經(jīng)濟(jì)問(wèn)題比較突出。能源是經(jīng)濟(jì)發(fā)展的重要保障因素,如何有效地利用能源對(duì)于解決環(huán)境問(wèn)題、能源與經(jīng)濟(jì)等問(wèn)題,保持經(jīng)濟(jì)的持續(xù)穩(wěn)步增長(zhǎng)具有重要意義。
一、計(jì)量模型的建立與檢驗(yàn)
(一)計(jì)量模型的建立
在經(jīng)濟(jì)學(xué)中,經(jīng)濟(jì)增長(zhǎng)可以用生產(chǎn)函數(shù)來(lái)刻畫。生產(chǎn)函數(shù)是表示在一定的技術(shù)條件下生產(chǎn)投入與產(chǎn)出之間的一種數(shù)量關(guān)系。本文應(yīng)用擴(kuò)展的柯布-道格拉斯(Cobb-Douglas)生產(chǎn)函數(shù)來(lái)刻畫生產(chǎn)過(guò)程,即:Y=AKαLβEγ(Nerlove ,1965) (1)
其中Y表示產(chǎn)出,A表示生產(chǎn)要素投入效率,K表示資本投入,L表示勞動(dòng)力投入,E表示能源投入,α、β、γ分別表示資本、勞動(dòng)力和能源的彈性系數(shù)。與傳統(tǒng)的柯布-道格拉斯生產(chǎn)函數(shù)Y=AKαLβ(2),簡(jiǎn)稱C-D生產(chǎn)函數(shù)相比可以發(fā)現(xiàn),Nerlove在原有C-D生產(chǎn)函數(shù)結(jié)構(gòu)的基礎(chǔ)上增加了和能源投入有關(guān)的乘子。假設(shè)用這兩個(gè)函數(shù)對(duì)同一生產(chǎn)過(guò)程進(jìn)行解釋,則可以看出Nerlove生產(chǎn)函數(shù)的本質(zhì)含義,就是將原本分?jǐn)傇谫Y本和勞動(dòng)力要素中的能源因素的影響從C-D生產(chǎn)函數(shù)中剝離出來(lái),形成獨(dú)立的第三要素。在當(dāng)今社會(huì),由于能源因素在生產(chǎn)過(guò)程中的重要性日漸增大,在研究生產(chǎn)過(guò)程中忽略能源的影響將會(huì)產(chǎn)生很大的誤差,所以對(duì)CD生產(chǎn)函數(shù)加以改進(jìn)是正確的。考慮到參數(shù)估計(jì)的方便性和經(jīng)濟(jì)學(xué)意義,我們對(duì)所采用的經(jīng)濟(jì)變量都取自然對(duì)數(shù)形式,并建立如下計(jì)量模型:
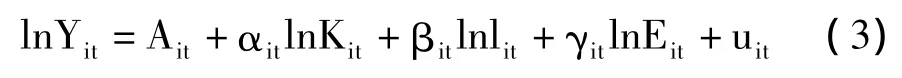
其中,i指地區(qū),t指時(shí)間。若 Ait= δ,αit=α,βit=β,γit=γ(δ,α,γ 為常數(shù),uit~ i.i.d.(0,σ2u)),則為混合回歸模型。若 Ait=δ+λi,αit=α,βit=β,γit=γ(δ,α,γ 為常數(shù),uit~ i.i.d.(0,σ2u)),則為個(gè)體固定效應(yīng)模型;若 Ait=δ+ηt,αit=α,βit=β,γit=γ(δ,α,γ 為常數(shù),uit~i.i.d.(0,σ2u)),則為時(shí)點(diǎn)固定效應(yīng)模型;若 Ait=δ+λi+ηt,αit=α,βit=β,γit=γ(δ,α,γ 為常數(shù),uit~i.i.d.(0,σ2u)),則為個(gè)體時(shí)點(diǎn)固定效應(yīng)模型;若 Ait=δ,αit=α,βit=β,γit=γ,uit=ut+wit(δ,α,γ 為常數(shù),ut為第 t時(shí)點(diǎn)的隨機(jī)干擾項(xiàng),wit~ i.i.d.(0,σ2w)),則為時(shí)間隨機(jī)效應(yīng)模型;若Ait=δ,αit=α,βit=β,γit= γ,uit=ui+vt+wit(δ,α,γ為常數(shù),ui,vt分別為個(gè)體和時(shí)點(diǎn)的隨機(jī)干擾項(xiàng),wit~ i.i.d.(0,σ2w)),則為個(gè)體時(shí)間隨機(jī)效應(yīng)模型。若Ait=δ,αit=αi,βit=βi,γit= γi(δ,α,γ 為常數(shù),uit~i.i.d.(0,σ2u)),則為個(gè)體固定參數(shù)的變系數(shù)回歸模型(SUR模型);若Ait=δ,αit=ˉα+ξαit,βit=ˉβ+ξβit,γit=ˉγ+ξγit(其中ξαit,ξβit,ξγit是均值為0,具有固定方差的隨機(jī)變量,uit~ i.i.d.(0,σ2u)),則為個(gè)體隨機(jī)參數(shù)的變系數(shù)回歸模型(Swamy模型);若 Ait=δ,αit=ˉα+ξαi+Ψαt,βit=ˉβ+ξβi+Ψβt,γit=ˉγ+ξγi+Ψγt(其中 ξαi,Ψαt,ξβi,Ψβt,ξγi,Ψγt是均值為 0,具有固定方差的隨機(jī)變量,uit~ i.i.d.(0,σ2u)),則為時(shí)點(diǎn)個(gè)體隨機(jī)參數(shù)的變系數(shù)回歸模型(Hsiao模型)。
(二)面板數(shù)據(jù)的單位根檢驗(yàn)
由于經(jīng)濟(jì)變量普遍存在著非平穩(wěn)的特征,所以同時(shí)間序列類似,在面板數(shù)據(jù)的分析中,首先也要做平穩(wěn)性檢驗(yàn),即單位根檢驗(yàn),否則非平穩(wěn)的面板數(shù)據(jù)對(duì)另一非平穩(wěn)的面板數(shù)據(jù)進(jìn)行回歸容易產(chǎn)生偽回歸問(wèn)題,其標(biāo)準(zhǔn)的t和F檢驗(yàn)是無(wú)效的。通過(guò)蒙特卡洛(Monte Carlo)實(shí)驗(yàn)發(fā)現(xiàn),與單變量時(shí)間序列的單位根檢驗(yàn)相比較,各種面板數(shù)據(jù)單位根檢驗(yàn)都不同程度地提高了單位根檢驗(yàn)的檢驗(yàn)功效。目前面板數(shù)據(jù)單位根檢驗(yàn)的方法比較多,其中Eviews6.0中支持的有:(a)Levin,Lin&Chu t*檢驗(yàn)(LLC檢驗(yàn));(b)Breitung t-stat檢驗(yàn);(c)Im,Pesaran and Shin W-stat檢驗(yàn)(IPS檢驗(yàn));(d)ADF -Fisher Chisquare檢驗(yàn);(e)PP-Fisher Chi-square檢驗(yàn)。其中(a)(b)檢驗(yàn)是基于同質(zhì)面板數(shù)據(jù)的,(c)(d)(e)檢驗(yàn)是基于異質(zhì)面板數(shù)據(jù)的。對(duì)于LLC檢驗(yàn),允許面板單位根檢驗(yàn)式中含有飄移項(xiàng)、時(shí)間趨勢(shì)項(xiàng)。盡管LLC檢驗(yàn)是應(yīng)用最廣泛的面板單位根檢驗(yàn),但LLC檢驗(yàn)也有局限性,該檢驗(yàn)嚴(yán)重依賴于截面的獨(dú)立性假設(shè),存在縱剖面相關(guān)的面板數(shù)據(jù)不可用,另外,假設(shè)所有縱剖面有或者都沒(méi)有單位根。針對(duì)于LLC檢驗(yàn)這一缺陷,IM、Pesaran和Shin提出了異質(zhì)面板的IPS單位根檢驗(yàn),IPS檢驗(yàn)允許縱剖面時(shí)間序列有單位根,通過(guò)蒙特卡洛實(shí)驗(yàn)發(fā)現(xiàn)IPS檢驗(yàn)比LLC檢驗(yàn)具有更良好的有限樣本的性質(zhì)。但I(xiàn)PS檢驗(yàn)同樣具有缺陷,即其要求數(shù)據(jù)是平衡面板數(shù)據(jù),對(duì)于非平衡面板數(shù)據(jù)則無(wú)法處理。針對(duì)于LLC檢驗(yàn)和IPS檢驗(yàn)的不足,基于異質(zhì)面板數(shù)據(jù)又出現(xiàn)了ADF-Fisher Chi-square檢驗(yàn)和PP-Fisher Chi-square檢驗(yàn)。對(duì)于Breitung檢驗(yàn),較LLC檢驗(yàn)和IPS檢驗(yàn)更優(yōu)于具有個(gè)體特征趨勢(shì)項(xiàng)的檢驗(yàn)。
(三)面板數(shù)據(jù)的協(xié)整檢驗(yàn)
自Engle和Granger(1978)發(fā)現(xiàn)時(shí)間序列的協(xié)整回歸以來(lái),有關(guān)經(jīng)濟(jì)變量間協(xié)整關(guān)系檢驗(yàn)方法的研究已經(jīng)成為非經(jīng)典計(jì)量經(jīng)濟(jì)學(xué)理論方法研究的核心問(wèn)題之一。眾所周知,時(shí)間序列觀測(cè)數(shù)據(jù)的長(zhǎng)度直接關(guān)系到協(xié)整關(guān)系檢驗(yàn)的效果,經(jīng)濟(jì)變量的觀測(cè)數(shù)據(jù)越長(zhǎng),協(xié)整檢驗(yàn)的功效就高,即協(xié)整檢驗(yàn)過(guò)程中犯第二類錯(cuò)誤的概率就越小(Pedroni,1995)。然而由于實(shí)際研究環(huán)境的限制,在許多經(jīng)濟(jì)問(wèn)題的研究中,經(jīng)濟(jì)變量的時(shí)間序列很短,所以制約了協(xié)整理論的發(fā)展。于是面板數(shù)據(jù)的協(xié)整理論便應(yīng)運(yùn)而生。面板協(xié)整檢驗(yàn)是用來(lái)檢驗(yàn)變量間長(zhǎng)期均衡關(guān)系的。其可分為兩類,一類是基于面板數(shù)據(jù)回歸式殘差數(shù)據(jù)單位根檢驗(yàn),即Engle-Granger(1987)兩步法的推廣。另一類是從推廣Johansen檢驗(yàn)的方向發(fā)展的面板協(xié)整檢驗(yàn)。相對(duì)于前一類檢驗(yàn),后者的協(xié)整檢驗(yàn)不僅能夠檢驗(yàn)多個(gè)協(xié)整關(guān)系,而且允許面板數(shù)據(jù)存在平穩(wěn)或非平穩(wěn)的共同成分。其中Eviews6.0支持的有:(a)Pedroni(Engle-Granger based)檢驗(yàn);(b)Kao(Engle-Granger based)檢驗(yàn)和(c)Fisher(Combined Johasen)檢驗(yàn)。其中(b)是針對(duì)于同質(zhì)面板數(shù)據(jù)的,(a)和(c)是針對(duì)于異質(zhì)面板數(shù)據(jù)的。本文采用(b),對(duì)經(jīng)濟(jì)增長(zhǎng)(LnY)和資本投入(LnK)、勞動(dòng)力(LnL)以及能源消費(fèi)(LnE)同時(shí)做協(xié)整檢驗(yàn)。
(四)面板數(shù)據(jù)的誤差修正模型及其因果檢驗(yàn)
協(xié)整的重要特征是它們的時(shí)間路徑是通過(guò)相對(duì)于長(zhǎng)期均衡的離差大小來(lái)影響的。畢竟,如果一個(gè)系統(tǒng)恢復(fù)到長(zhǎng)期均衡,則至少有一些變量的變化一定會(huì)對(duì)非均衡的大小做出響應(yīng)。
這類將均衡離差的影響納入系統(tǒng)短期動(dòng)態(tài)變化過(guò)程中的模型稱為誤差修正模型(Error Correction Model,ECM)。ECM的思想可簡(jiǎn)單概括為,某一時(shí)期出現(xiàn)的非均衡將在下一期予以修正。在協(xié)整關(guān)系成立的前提下,可建立如下面板數(shù)據(jù)誤差修正模型:
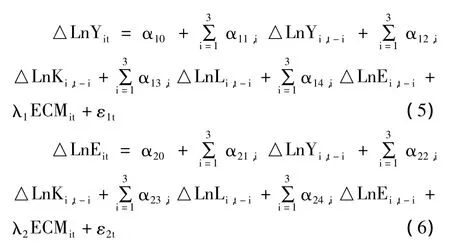
在(5)式和(6)式中,Δ表示一階差分運(yùn)算(下同),ECTit表示長(zhǎng)期均衡誤差。誤差修正模型為研究變量之間的因果關(guān)系開(kāi)辟了新途徑。在(5)式中,如果α14顯著異于0,則能源消費(fèi)是經(jīng)濟(jì)增長(zhǎng)的短期Granger原因;如果λ1顯著不為0,則能源消費(fèi)是經(jīng)濟(jì)增長(zhǎng)的長(zhǎng)期Granger原因。反之,如果α14顯著等于0,則能源消費(fèi)不是經(jīng)濟(jì)增長(zhǎng)的短期Granger原因;如果λ1顯著等于0,則能源消費(fèi)不是經(jīng)濟(jì)增長(zhǎng)的長(zhǎng)期Granger原因。同理,可檢驗(yàn)經(jīng)濟(jì)增長(zhǎng)是否是能源消費(fèi)的長(zhǎng)期或短期Granger原因。
二、實(shí)證分析
(一)樣本選擇與數(shù)據(jù)描述
本文各經(jīng)濟(jì)指標(biāo)的數(shù)據(jù)主要來(lái)源于《內(nèi)蒙古統(tǒng)計(jì)年鑒》(2002-2011),數(shù)據(jù)區(qū)間為2001-2010,指標(biāo)的選取與處理如下:
1.國(guó)內(nèi)生產(chǎn)總值Y:通過(guò)Y指數(shù)平減,化成以2001年為基期的不變價(jià)的Y,剔除了價(jià)格因素的影響(單位:億元)。
2.資本存量K:本文采用每年年底實(shí)際庫(kù)存與新增固定資產(chǎn)投資總額(I)的和作為每年的實(shí)際資本存量。為使數(shù)據(jù)具有可比性,使用官方公布的固定資產(chǎn)投資價(jià)格指數(shù),通過(guò)I指數(shù)平減,把每年的新增固定資產(chǎn)投資總額化成以2001年為基期的不變價(jià)的。計(jì)算每年資本存量時(shí),將t時(shí)期的資本存量定義為t-1時(shí)期資本存量加投資減折舊,即:

(7)式中,Kit是i地區(qū)t年的資本存量,Iit是i地區(qū)t年的新增固定資產(chǎn)投資總額,δ是固定資產(chǎn)折舊率。根據(jù)歷史數(shù)據(jù),固定資產(chǎn)折舊率平均在5%左右,因此2001年以來(lái)的固定資產(chǎn)折舊率都定為5%。另外,以2001年的固定資產(chǎn)投資總額作為初始資本存量。以后年份的資本存量都按(7)式計(jì)算而得到(單位:萬(wàn)元)。
3.全社會(huì)職工工資總額作為勞動(dòng)力L:本文使用全社會(huì)職工工資總額作為勞動(dòng)力資本。這里不是用從業(yè)人員人數(shù)作為勞動(dòng)力變量數(shù)據(jù),是因?yàn)槿藬?shù)變化只能反應(yīng)勞動(dòng)力數(shù)量的變化,但不能反映勞動(dòng)力質(zhì)量的變化,而勞動(dòng)力作為影響產(chǎn)出量的一大要素最主要的原因是勞動(dòng)力質(zhì)量的變化對(duì)產(chǎn)出量有很大影響(國(guó)涓,2008)。在使用職工平均工資這一數(shù)據(jù)時(shí),也同樣要考慮數(shù)據(jù)的可比性,以2001年為基期,換算成不變價(jià)的職工工資總額(單位:萬(wàn)元)。
4.能源消費(fèi)總量作為能源E:考慮到近年來(lái)中國(guó)能源生產(chǎn)和消費(fèi)總量中,煤炭和石油供需存在明顯低估。相比之下,由計(jì)算機(jī)直接讀出的電力消費(fèi)量數(shù)據(jù)就相當(dāng)準(zhǔn)確。此外電力消費(fèi)是中國(guó)能源消費(fèi)的主要方式。因此,使用電力消費(fèi)更能準(zhǔn)確反映能源消費(fèi)與經(jīng)濟(jì)增長(zhǎng)之間的內(nèi)在聯(lián)系(林伯強(qiáng),2003),所以本文采用2001-2010年各地區(qū)電力消費(fèi)量作為能源消費(fèi)量(單位:億千瓦小時(shí))。
(二)面板數(shù)據(jù)單位根檢驗(yàn)
因?yàn)槲覀兯⒌哪P褪蔷€性模型(取對(duì)數(shù)后),所以先要檢驗(yàn)數(shù)據(jù)的平穩(wěn)性,即先對(duì)各個(gè)變量進(jìn)行單位根檢驗(yàn)。可以說(shuō)面板數(shù)據(jù)的單位根檢驗(yàn)也是進(jìn)行面板協(xié)整檢驗(yàn)分析的必要前提。根據(jù)前面介紹的單位根檢驗(yàn)方法,利用Eviews6.0我們對(duì)呼包鄂地區(qū)的國(guó)民生產(chǎn)總值的(Y)和資本(K)、勞動(dòng)力(L)、能源消費(fèi)(E)的自然對(duì)數(shù)序列(分別記為L(zhǎng)nYit、LnKit、LnEYit、LnLiti)進(jìn)行了單位根檢驗(yàn),看它們是否是單位根過(guò)程,即檢驗(yàn)它們各自的平穩(wěn)性。考慮到呼包鄂地區(qū)在經(jīng)濟(jì)總量等方面的相似性,我們采用同質(zhì)面板的Levin,Lin&Chu t*檢驗(yàn)即LLC檢驗(yàn)(見(jiàn)表1)。
通過(guò)對(duì) LnYit、LnKit、LnEYit、LnLiti序列的檢驗(yàn),在5%的顯著水平上,序列水平值均不平穩(wěn),一階差分序列均平穩(wěn),則可以進(jìn)行協(xié)整檢驗(yàn)了。

表1
(三)面板數(shù)據(jù)的協(xié)整檢驗(yàn)
首先,我們來(lái)建立計(jì)量經(jīng)濟(jì)學(xué)模型。考慮到呼包鄂地區(qū)在經(jīng)濟(jì)總量等方面的相似性,我們建立同質(zhì)面板數(shù)據(jù)的計(jì)量模型。至于是固定效應(yīng)模型還是隨機(jī)效應(yīng)模型,我們可以用Eviews6.0提供的似然比檢驗(yàn)(即F檢驗(yàn))的方法來(lái)確定。下面進(jìn)行個(gè)體時(shí)點(diǎn)固定效應(yīng)模型的設(shè)定檢驗(yàn):
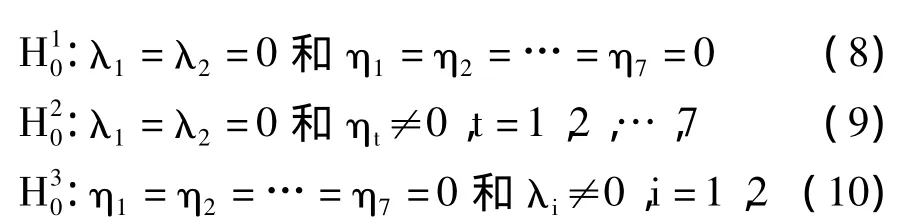
顯然,檢驗(yàn)假設(shè)(9)的目的是推斷存在時(shí)點(diǎn)效應(yīng)的情況下,判斷模型是否包含個(gè)體效應(yīng);檢驗(yàn)假設(shè)(10)正好與上相反。于是,在(8)假設(shè)下
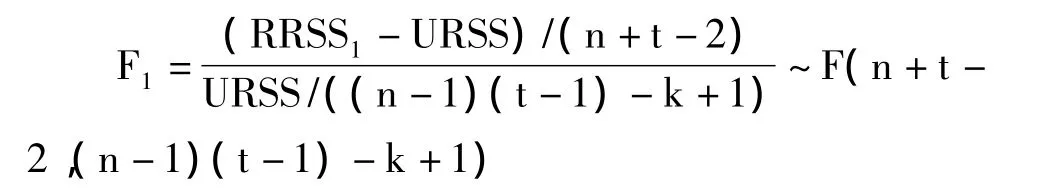
其中,RRSS1為無(wú)約束的殘差平方和,RUSS為混合回歸殘差平方和,n=3,t=8,K=1。
同理,在假設(shè)(9)、(10)下可分別建立:
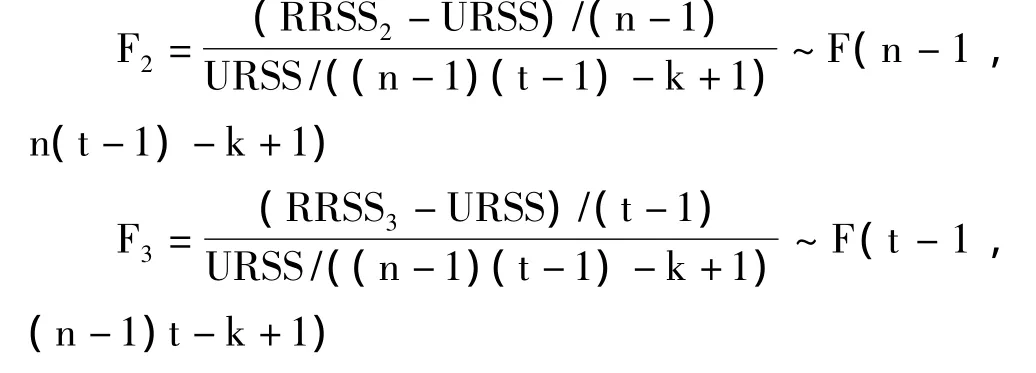
其中RRSS是受約束的回歸殘差平方和,URSS為無(wú)約束的回歸殘差平方和,k為待估參數(shù)個(gè)數(shù)(不包括常數(shù)項(xiàng))。按照Hendry的“一般到特殊”的建模思想,通過(guò)計(jì)算得:F1=26.57 >F(9,14)=2.12 ,所以拒絕假設(shè)(8),建立個(gè)體時(shí)點(diǎn)的混合固定效應(yīng)模型,即:

其中個(gè)體固定影響效用為:呼和浩特-0.11,包頭 -0.36,鄂爾多斯0.47。
時(shí)點(diǎn)固定影響效用為:

2001 2002 2003 2004 2005 2006 2007 2008-0.26 -0.22 -0.09 -0.12 -0.03 0.17 0.22 0.33
下面對(duì)上述已經(jīng)建立的計(jì)量模型依Eviews6.0進(jìn)行協(xié)整檢驗(yàn)。采用Kao檢驗(yàn),t統(tǒng)計(jì)量的值為-2.23,所以在5%的顯著性水平上,拒絕原假設(shè)(原假設(shè)為序列不存在協(xié)整),所以序列LYit和LKit、LEYit、LLiti具有協(xié)整關(guān)系。
(四)面板數(shù)據(jù)的誤差修正模型及其因果檢驗(yàn)
通過(guò)面板數(shù)據(jù)協(xié)整檢驗(yàn),我們建立了兩個(gè)協(xié)整方程,但由于時(shí)間跨度較小,需通過(guò)誤差修正模型來(lái)進(jìn)一步檢驗(yàn)兩個(gè)協(xié)整方程的可靠性。先根據(jù)(5)式檢驗(yàn)呼包鄂地區(qū)能源消費(fèi)是否為經(jīng)濟(jì)增長(zhǎng)的Granger原因,再根據(jù)(6)式檢驗(yàn)呼包鄂地區(qū)經(jīng)濟(jì)增長(zhǎng)是否為能源消費(fèi)的Granger原因。作為滿足誤差項(xiàng)經(jīng)典假設(shè)的要求,將滯后項(xiàng)m定為1。在以經(jīng)濟(jì)增長(zhǎng)為因變量的誤差修正模型(5)中,ECM項(xiàng)回歸系數(shù)λ1為0.18,其t值為2.11,在10%的顯著性水平下不為0,所以誤差糾正機(jī)制發(fā)生;而變量△LnEt-1的回歸系數(shù)α14在10%的水平上顯著為0,所以對(duì)呼包鄂地區(qū)來(lái)說(shuō),在長(zhǎng)期,能源消費(fèi)是經(jīng)濟(jì)增長(zhǎng)的Granger原因,而在短期則不是。同理,在以能源消費(fèi)為因變量的誤差修正模型(6)中,ECM項(xiàng)回歸系數(shù) λ2為 0.44,其 t值為0.27;變量△LnEt-1的回歸系數(shù) α24為 -1.68,其 t值為 -1.09,所以經(jīng)濟(jì)增長(zhǎng)無(wú)論短期還是長(zhǎng)期都不是能源消費(fèi)的Granger原因。
三、結(jié)論
通過(guò)對(duì)能源消費(fèi)與經(jīng)濟(jì)增長(zhǎng)的關(guān)系進(jìn)行了實(shí)證分析,我們發(fā)現(xiàn)能源消費(fèi)是經(jīng)濟(jì)增長(zhǎng)的單向Granger原因。進(jìn)入新世紀(jì),尤其是“十五”以來(lái),呼和浩特、包頭和鄂爾多斯能源消費(fèi)分別由2005年的1416.65萬(wàn)噸標(biāo)準(zhǔn)煤、2380.10萬(wàn)噸標(biāo)準(zhǔn)煤和1300.66萬(wàn)噸標(biāo)準(zhǔn)煤增至2010年的2373.93萬(wàn)噸標(biāo)準(zhǔn)煤 、4018.3萬(wàn)噸標(biāo)準(zhǔn)煤和2704.37萬(wàn)噸標(biāo)準(zhǔn)煤,漲幅近80%;煤炭消費(fèi)量分別由2005年的2363.14萬(wàn)噸和1765.53萬(wàn)噸、2466.33萬(wàn)噸增至2010年的3637.47萬(wàn)噸 、3823.23萬(wàn)噸和4332.43萬(wàn)噸,漲幅也達(dá)到了80%。能源強(qiáng)度由2005年1.90噸標(biāo)準(zhǔn)煤/萬(wàn)元、2.80噸標(biāo)準(zhǔn)煤/萬(wàn)元和2.19噸標(biāo)準(zhǔn)煤/萬(wàn)元下降到1.47噸標(biāo)準(zhǔn)煤/萬(wàn)元 、2.01噸標(biāo)準(zhǔn)煤/萬(wàn)元 和1.59噸標(biāo)準(zhǔn)煤/萬(wàn)元,但下降幅度卻只有近30%。這充分說(shuō)明相對(duì)能源利用效率降低了。能源利用效率的降低意味著資源環(huán)境壓力的增大,因此,提高能源利用效率,不僅有助于釋放經(jīng)濟(jì)發(fā)展?jié)摿Γ€可以解決經(jīng)濟(jì)社會(huì)發(fā)展越來(lái)越受到的資源環(huán)境問(wèn)題。
[1] 林伯強(qiáng).電力消費(fèi)與中國(guó)經(jīng)濟(jì)增長(zhǎng)——基于生產(chǎn)函數(shù)的研究[J].管理世界,2003,(11).
[2] 馬超群,儲(chǔ)慧斌,李科,周四清.中國(guó)能源消費(fèi)與經(jīng)濟(jì)增長(zhǎng)的協(xié)整與誤差校正模型研究[J].系統(tǒng)工程,2004,(10).
[3] 韓智勇,魏一鳴,焦建玲.中國(guó)能源消費(fèi)與經(jīng)濟(jì)增長(zhǎng)的協(xié)整性與因果關(guān)系檢驗(yàn)[J].系統(tǒng)工程,2004,(22).
[4] 周少甫,閔娜.中國(guó)經(jīng)濟(jì)增長(zhǎng)與能源消費(fèi)關(guān)系的協(xié)整分析[J].當(dāng)代經(jīng)濟(jì),2005,(6).

