基于P-S-N曲線的三參數法估計葉片最低疲勞極限的實踐研究

李 勛，張東明，姜 睿

(沈陽發動機設計研究所，遼寧 沈陽110015)

1 引言

葉片是航空發動機的關鍵零件，一臺發動機的葉片多以千計，其中任何一個葉片發生破壞，都可能會造成空中停車甚至更為嚴重的事故，因此，測試葉片的疲勞性能、保證葉片使用的可靠性就顯得尤為重要。

工程上通常用升降法或50%存活率的S-N曲線估計葉片的疲勞壽命，但如果單純以這種中值壽命作為航空發動機葉片壽命估算的依據，則往往偏于危險。因為這樣做意味著有一半的葉片將在達到預期壽命N0之前會過早地發生破壞而危及飛行安全。為了對葉片疲勞性能進行有效評估，本世紀初，國內出現了葉片最低疲勞極限的概念，相關的試驗工作也逐步發展起來。

2 最低疲勞極限

疲勞極限是指材料或構件經受無限壽命循環而不發生破壞所能承受的最大交變應力。一般將疲勞壽命為107～108循環所對應的疲勞強度稱為疲勞極限。最低疲勞極限的概念，最早出現在國外某型發動機的關于葉片疲勞強度檢查的技術條件中，是指必須滿足葉片安全強度儲備要求所允許的最小疲勞極限值。近年來，在我國航空發動機研制領域，參照該檢驗要求并結合工程實踐經驗，對最低疲勞極限有了一個全新的認識，并逐步把它作為評價葉片疲勞性能優劣的一個重要指標。工程上通常把等載荷作用下連續n個葉片的壽命達到或超過預期壽命的這一載荷值作為該葉片的最低疲勞極限，它既有循環基數要求，又有試件個數和連續性要求。

在測試最低疲勞極限的常規試驗中，不僅要求有大量的試驗件，而且試驗周期均較長。當兩者不能同時滿足工程需要時，利用本文提出的基于P-S-N[1]曲線的三參數估計法能以較少的試件數對其最低疲勞極限做出快速而有效的估計。

3 三參數估計法

3.1 基本思想

利用葉片99.9%存活率的S-N曲線方程估計滿足預期壽命的應力值，以作為該葉片的最低疲勞極限。本文將依據小樣本理論[2]、利用三參數估計法測定99.9%存活率的S-N曲線方程，進而獲得葉片的最低疲勞極限，旨在降低試驗費用、縮短試驗周期以滿足工程需要。

根據Bayes理論[3]和加速壽命試驗理論[4]，并結合工程實踐經驗，對三參數估計法作如下假設：

(1)假定葉片的S-N曲線以某一函數關系表示，即曲線方程為

式中：σ為N→∞時的應力，σ、A、a均為常數。

(2)假定不同存活率P的P-S-N曲線函數形式相同，同樣可以表示為

式中：σP由被測葉片的疲勞試驗結果確定。

(3)假定應力σ或lg σ遵循正態分布[5]。常數A、a由被測葉片或與被測葉片結構相似[6]葉片(指葉片材料與加工工藝相同、型面近似的葉片)的疲勞試驗結果確定，σ由被測葉片的疲勞試驗結果確定。

3.2 實施步驟

(1)確定常數A、a

首先將式(1)變換為S/σ-1=A/Na，兩邊同時取對數并令 YS=-lg(S/σ-1)，則有：

上式表明YS與lg N成直線關系。這樣可利用不同應力水平 S0、S1、S2、…、Sk下，循環次數分別為n0、n1、n2、…、nk的一組常規試驗數據(4～6 個子樣即可)來確定常數A和a。此時式(3)YS中的變量σ可由試選法依據經驗任意給出。

(2)確定常數σ

由于S-N曲線方程中的常數A、a已經確定，則式(1)可變換為：

其子樣平均值為：

子樣標準差為：

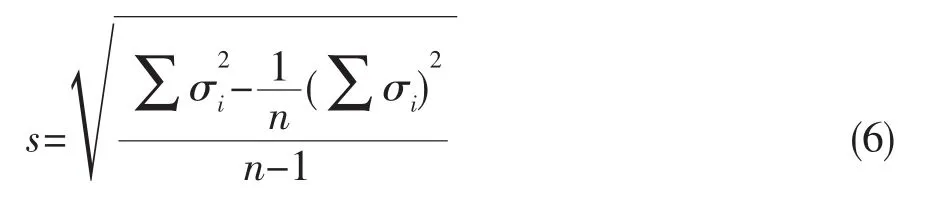
(3)確定P-S-N曲線方程，求最低疲勞極限

將 σP、A、a各值帶入式(2)中，即可得到某一 P的P-S-N曲線方程。當置信度為90%、存活率為99.9%時，滿足預期壽命N0的應力值可根據式(2)得出，即最低疲勞極限S-1可表示為：

3.3 與常規方法的比較

常規方法測試葉片的最低疲勞極限，通常是從較高的應力載荷開始，逐級降低載荷標準，直到滿足最低疲勞極限要求的載荷出現為止，這意味著試驗要從葉片的中等壽命區開始，逐步向長壽命區過渡。試驗中載荷級差的選取尤為重要，如果級差過大，得出的最低疲勞極限偏保守，會給結構設計帶來困難；級差偏小，則所需試件數量就會成倍增加。可見，常規試驗法不僅對試驗者提出了較高要求，同時也會耗費大量的試驗費用和試驗時間。

三參數估計法的試驗主要在葉片的中等壽命區進行，不僅試件個體的試驗時間短，而且需要的試件數量也相對較少。這樣不僅可以更好地滿足工程需要，而且還可以通過P-S-N曲線方程對葉片疲勞性能做出較全面的評價。不過，當葉片由于材料、加工等原因造成的疲勞性能分散度特別大時，三參數估計法的誤差可能會比較大，而此時常規試驗的誤差相對較小。

4 應用實例

下面通過一組實例來分析比較該方法在實際工程上的應用。該組數據為某發動機高壓壓氣機第3級轉子葉片的疲勞試驗數據(見表1和表2)，該級葉片材料為鈦合金，預期壽命N0=3×107。根據工程經驗和初步試驗結果(表1)，估計σ在450～550 MPa之間；算例數據處理中試選σ=550 MPa。根據表1數據由圖解法(見圖1)或解析法可求出a=0.457 1，A=68.960 4。

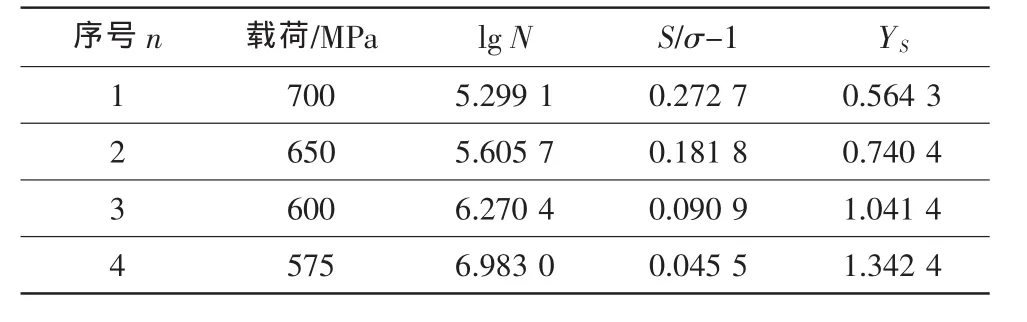
表1 不同載荷下的壽命試驗Table 1 Results of life tests at different loads

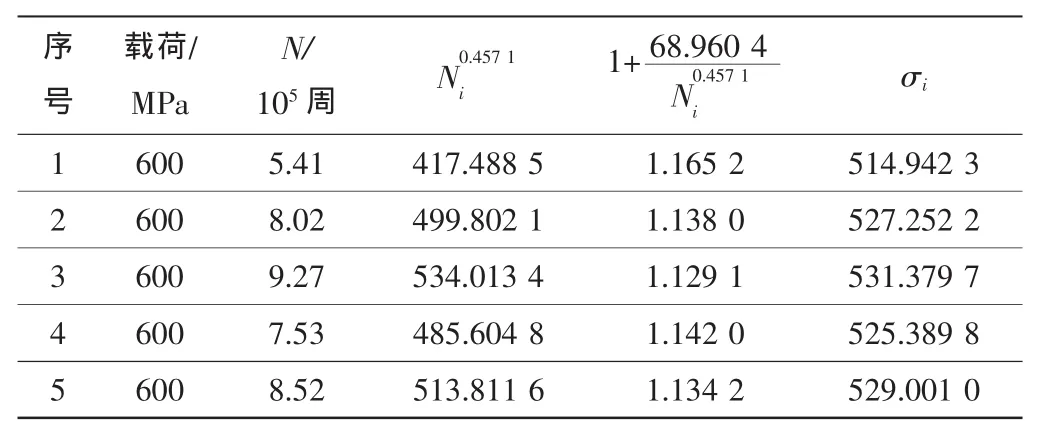
表2 相同載荷下的壽命試驗Table 2 Results of life tests at 600 MPa

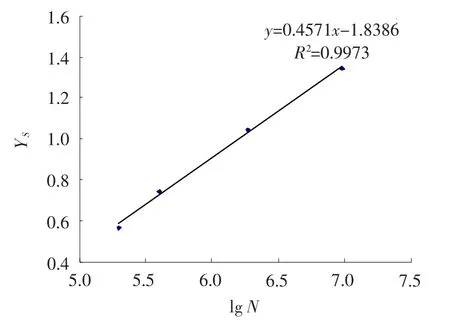
圖1 YS與lg N的數據擬合Fig.1 The curve of YSvs lg N

由表2中數據可得：

子樣平均值

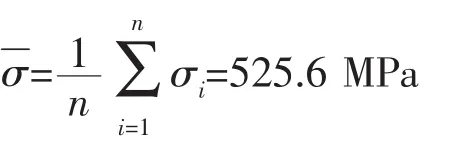
子樣標準差

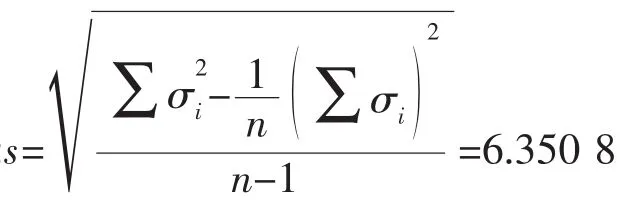
選取置信度為95%，存活率為99.9%，對于n=5，由文獻[1]查得k=-7.532。則有：

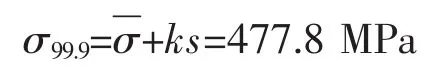
最低疲勞極限為：

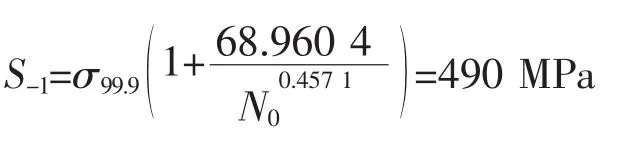
另外，若算例數據處理中試選σ=480 MPa，則S-1=478 MPa；若試選σ=450 MPa，則σ=475 MPa。而由常規方法實測該級葉片最低疲勞極限為500 MPa。由此可見，如果σ的取值在合適的估值區間內，三參數法的估計結果與實測值偏差不大，完全能滿足工程需要。

5 結論

(1)本文提出的基于P-S-N曲線的三參數試驗法能夠以較少的試件數量、較短的試驗時間獲得葉片的最低疲勞極限，不僅試驗費用低，而且置信度高，與常規方法獲得的試驗數據相比，結果令人滿意，比較適合工程需要。

(2)通過該試驗方法確定的P-S-N曲線，可為安全評估葉片在不同壽命區的疲勞性能提供參考。

(3)該試驗方法中要試選疲勞極限σ，該值對估值誤差有一定的影響，需要一定的工程經驗；另外，當葉片由于材料、加工等原因造成的疲勞性能分散度特別大時，三參數法的估計誤差還有待深入研究。

[1]高鎮同.疲勞性能測試 [M].北京：國防工業出版社，1980.

[2]馮師顏.誤差理論與實驗數據處理[M].北京：科學出版社，1964.

[3]Artymiak P，Bukowski L，Feliks J，et al.Determination of S-N Curves with the Application of Artificial Neural Networks[J].Fatigue&Fracture of Engineering Materials and Structures，1999，22(8)：723—728.

[4]Lipson C，Sheth N J.Statistical Design and Analysis of Engineering Experiments[M].New York：McGraw-Hill，1973.

[5]高鎮同，熊峻江.疲勞可靠性[M].北京：北京航空航天大學出版社，2000.

[6]Nakazawa H，Kodama S.Statistical Research on Fatigue and Fracture [M].New York：Elsevier Applied Science，1987.