基于小波降噪與分形理論的滾動軸承故障診斷

卓蒙蒙，張曉光，姬程鵬，雷大江

(1.中國礦業大學 機電工程學院，江蘇 徐州 221008；2.大連交通大學 管理學院，遼寧 大連 116052)

滾動軸承故障振動信號中往往含有大量的噪聲信號，且是非線性與不穩定的。傳統的故障診斷方法往往將非線性問題通過數學模型轉換為線性問題，雖然診斷運算簡便，但缺乏可靠性與準確度。分形理論的出現為認識與研究非線性系統的復雜性和隨機性提供了有力的數學依據[1]，其研究對象是傳統歐幾里德幾何和微積分方法不能描述的一大類不光滑或不規則集合和函數的結構，將分形理論應用于復雜機械故障診斷是目前故障診斷領域的熱點。

滾動軸承的振動信號在一定的時域長度內具有自相似性，因此可以將分形維數作為振動信號的特征參數進行故障診斷。然而研究表明[2],如果振動信號中含有大量的噪聲信號，則計算出來的分形維數偏大，影響故障診斷的準確性。因此利用分形理論對故障信號診斷之前，需先對信號降噪處理。下文通過小波對振動信號進行降噪，然后利用分形理論對故障信號進行分類與診斷。

1 小波降噪

在信號處理領域，小波降噪已得到越來越廣泛的應用。目前，常用的小波降噪方法有小波分解重構法、非線性小波變換閾值法、平移不變量小波法以及小波變換模極大值法[3]。其中非線性小波變換閾值法由于能獲得信號的近似最優估計而得到廣泛的應用。

設帶噪聲的信號為

yi=xi+mi,

(1)

式中：mi為方差為σ2的高斯白噪聲，即N(0,σ2)；yi為含有噪聲的信號；xi為原始信號。

小波閾值降噪的基本原理是：首先將含有噪聲的信號進行小波分解，如果噪聲信號遠小于原始信號，則分解出來的噪聲信號的小波系數也同樣小于原始信號的小波系數，選定1個特定的閾值，將小于閾值的小波系數重置為零，而保留大于閾值的小波系數。然后對篩選后的小波系數進行小波重構，即可得到降噪后的信號。小波去噪的難點是閾值與閾值函數的選取[1-5]，相比較而言，經軟閾值處理后的信號更加光滑，因此選用軟閾值作為閾值函數，固定閾值作為閾值λ對含有噪聲的振動信號降噪。

2 分形維數及其計算[2]

維數是空間和客體的重要幾何參數，在狀態空間中反映了描述該空間所需變量的個數。分形維數是定量描述分形特征的重要參數，常見的有盒維數、廣義維數、信息維數和關聯維數。其中關聯維數可以由觀測得到的一維時間序列利用G-P算法直接計算，因此，常用關聯維數作為區分不同故障的依據。

關聯維數的具體形式為：假設{xk}為給定的一維時間序列，其中k=1，2，…，N。選取時間延遲τ，采樣間隔t，采用重構相空間維數m對{xk}相空間進行重構，重構結果記為Xn(m,τ)=(xn,xn+1,…,xn+(m-1)τ)，其中n=1，2，…，N-m+1。選取重構相空間中任意2點Xi，Xj，計算2點之間的距離ri,j=‖Xi-Xj‖，選取正數r，計ri,j小于r的對數占全部點對數的比例為C(r)，則C(r)為

Xj‖)。

(2)

H為Heaviside函數，即

H(r-‖Xi-Xj‖)=

(3)

則關聯維數D可表示為

(4)

也就是說，如果以lnC(r)為縱軸，以lnr為橫軸，則曲線的斜率即為D。

3 分形診斷分類原理[6]

故障診斷實際上包括特征提取與故障分類2個過程，然而同一種故障在不同狀態下的表現形式可能不同，但是其特征參數卻表現出共性，根據這些共性就能區別其他類型的故障。當利用振動信號進行故障診斷時，可以對系統的不同故障建立特征模式，再由這些特征模式組建特征空間，每種特征對應于模式空間中的1個點，模式空間建立如下：

M(Xi)=[x1,x2,…,xj]T。

(5)

(6)

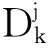
4 故障診斷示例

以某礦主井提升機用雙列向心球面滾子軸承3003246為例，軸承尺寸為Φ320 mm×Φ580 mm×208 mm，采樣頻率為2 000 Hz，采樣點數為1 024。圖1為未經降噪的原始振動信號；選用固定閾值、軟閾值函數對原始信號進行降噪，降噪后的時域波形如圖2所示。

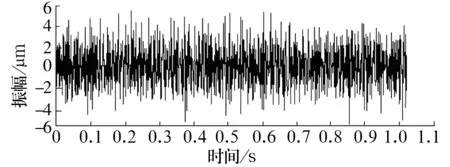
圖1 實測振動信號時域圖

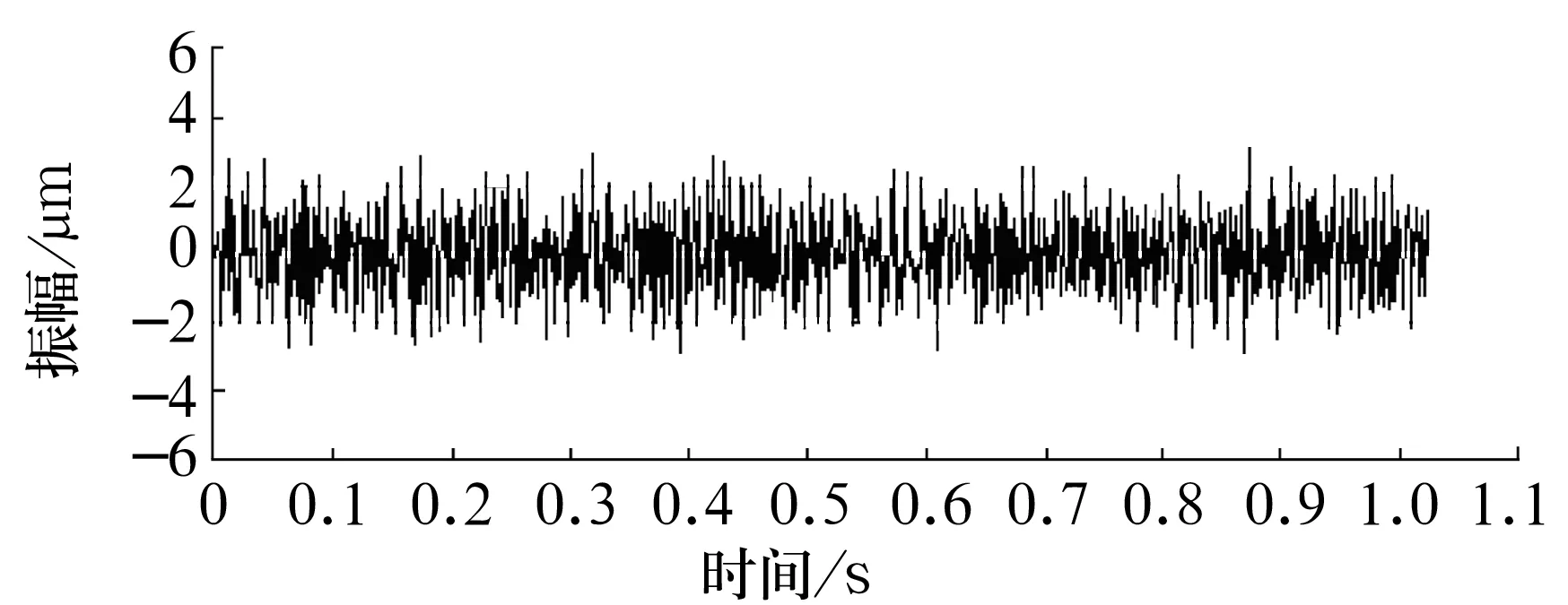
圖2 小波降噪后信號時域圖

圖3～圖5分別為降噪后的軸承外圈、內圈裂紋時域圖和待檢信號時域圖。

圖3 外圈裂紋降噪后時域圖

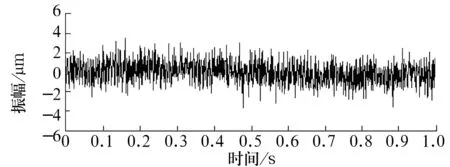
圖4 內圈裂紋降噪后時域圖

圖5 待檢信號振動時域圖

選取不同的重構空間維數m對降噪后的信號求關聯維數，結果如圖6所示。

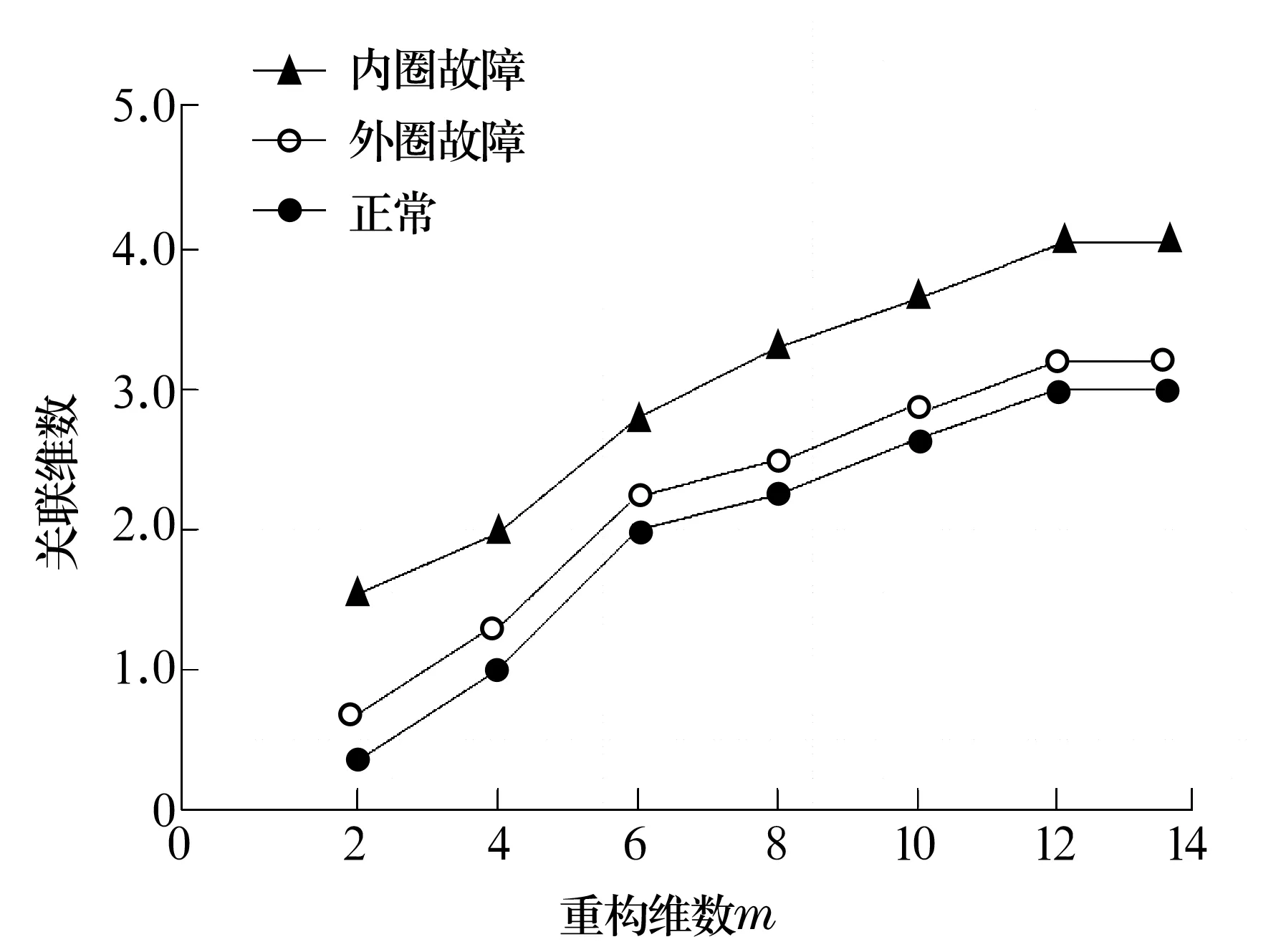
圖6 重構維數選擇示意圖

由圖6可以看出，隨著重構維數m的增大，關聯維數有增大的趨勢，同時結合不同軸承狀態的lnr-lnC(r)圖(圖7～圖9)可以看出，當m增大到12時，關聯維數趨于穩定，所以在此選用m=12計算各軸承狀態的關聯維數。

圖7 正常信號關聯維數雙對數圖

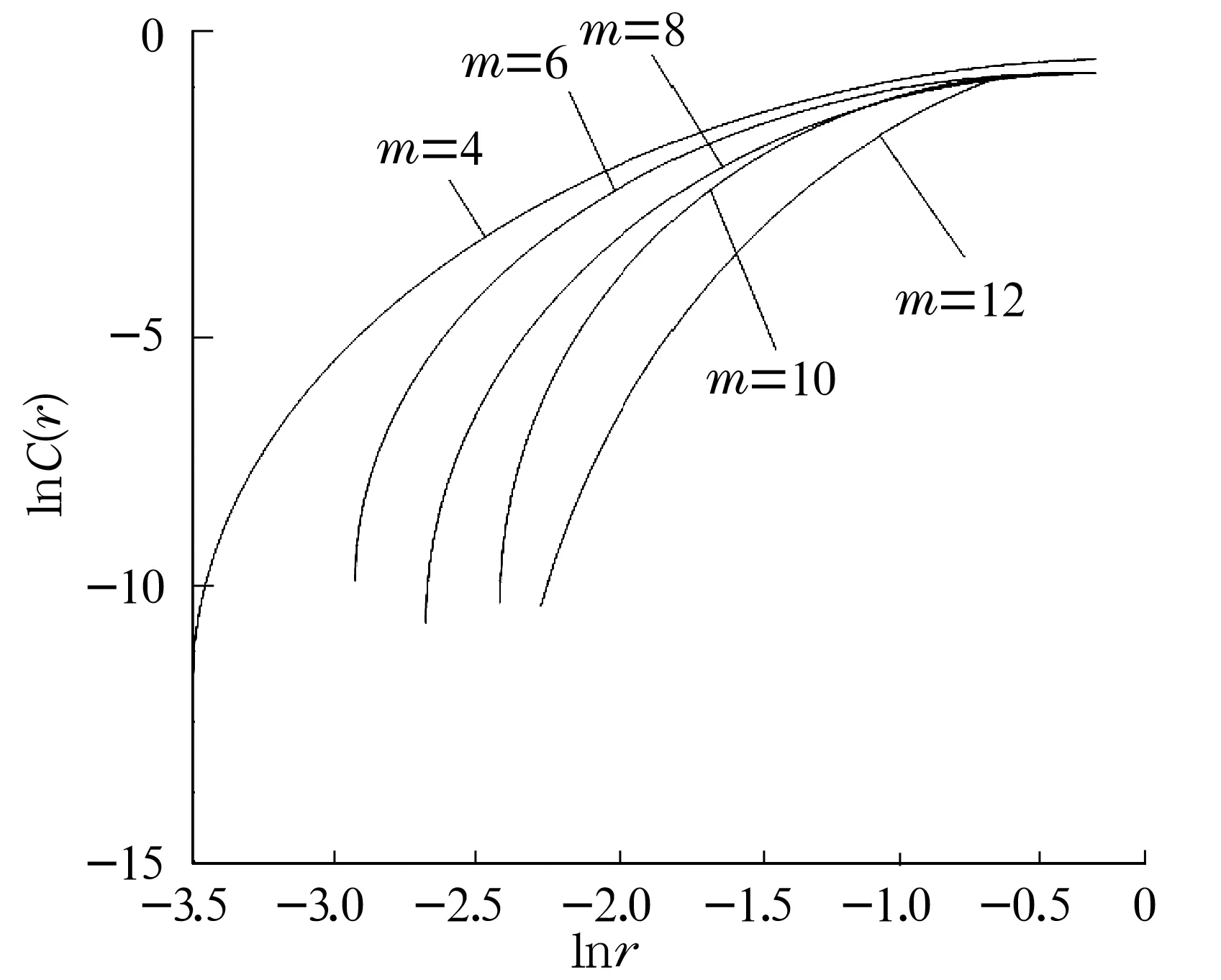
圖8 內圈故障信號關聯維數雙對數圖

圖9 外圈故障信號關聯維數雙對數圖

對采樣信號截取5段分別計算關聯維數，然后求平均數。結果見表1。

由表1可以看出，軸承正常時關聯維數最小，當內圈或外圈發生故障時，關聯維數有不同程度地增大。標準差越小說明離平均值越接近，誤差越小。因此可以通過計算關聯維數判斷軸承是否發生故障。

表1 不同工況關聯維數

用同樣的方法求信號待檢的關聯維數，并計算與軸承狀態的距離函數，結果見表2。由表2可知，待檢信號與外圈裂紋的距離函數最大，因此可判斷待檢信號屬于外圈裂紋故障，檢測結果與實際相吻合。

表2 待檢信號與不同軸承狀態的距離函數 R(j,x)

5 結束語

通過上述數據分析可知，可以將關聯維數作為振動信號的特征量，但計算關聯維數之前應先對信號降噪，當軸承發生故障時，關聯維數增大，通過計算與已知故障的距離函數即可判斷出待檢信號的故障類型。