基于數理統計理論的中國軸承產業專利趨勢預測
牛青波,賈現召,葉軍
(1. 河南科技大學 機電工程學院,河南 洛陽 471003;2.洛陽軸研科技股份有限公司,河南 洛陽 471039;3.河南省機械設計及傳動系統重點實驗室,河南 洛陽 471003)
隨著知識產權主體地位的不斷提升,國內、外企業也都把專利作為市場競爭的另一利器,專利預測則成為企業或政府制定專利戰略規劃和決策時考慮的必要因素。對專利文獻數據進行統計只能了解在過去一段時間內的專利申請和研發趨勢情況,而通過對已知的專利文獻數據進行統計則能夠對未來該企業或地區相關專利情況做出預測,有效幫助企業或政府制定相應的戰略決策。但由于專利申請數據的變化受國家政策、企業技術投入、企業管理模式改變及技術人員數量等多種因素影響,無法判斷影響專利申請數據的主要因素,統計理論中無法使用回歸預測分析方法。下文采用專利信息定量分析方法中的時間序列分析預測以及灰色系統分析預測方法,預測國家或競爭對手專利申請數量的發展趨勢。
1 專利統計數據預處理
通過中國知識產權網專利數據庫[1]對1985年4月1日—2010年12月31日間公開的專利申請進行檢索,檢索名稱定義為“軸承 or 保持架 or 保持器 or 滾動體”,摘要定義為“軸承”,或者檢索式定義為“摘要=(軸承) and 名稱=(軸承 or 保持架 or 保持器 or 滾動體)”。由于中國《專利法》規定,發明專利申請一般自申請日起滿18個月才公告,因此2010年的專利申請公開有滯后,目前公開的專利數據不能完全反映2010年度的專利申請情況。為此利用專利管理圖僅對1985年4月1日—2008年12月31日的專利申請進行趨勢研究,并對2009年和2010年中國軸承產業技術領域的中國專利申請趨勢、國外在華申請趨勢及國內專利申請趨勢進行預測。
對于專利統計數據,充分考慮樣本的代表性,使其能夠有效反映專利申請數據的變化規律,采用研究對象的總和作為數據樣本,統計數據見表1~表3。以下的分析計算中均以當年專利數量作為統計分析的原始序列數據。
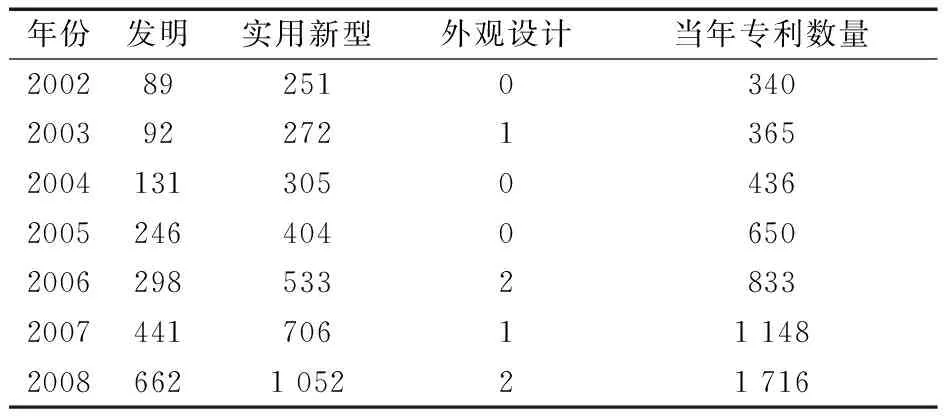
表1 2002—2008年中國軸承技術領域專利申請統計表

表2 2002—2008年國內專利申請人軸承技術領域專利申請統計表
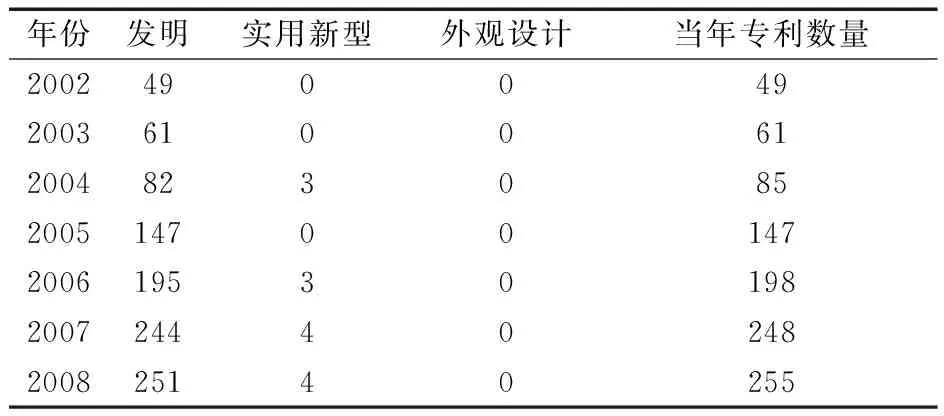
表3 2002—2008年國外專利申請人軸承技術領域專利申請統計表
2 基于Logistic生長曲線和灰色動態模型的預測
時間序列分析預測是將預測目標的統計數據按照時間順序排列成為時間序列,分析其隨時間的變化趨勢,預測目標的未來值。生長曲線預測方法是技術預測中的一種常用方法,特別是Logistic曲線,其對于大多數產業統計時系列數據具有高度的適用性[2]。由于專利件數申請量成因復雜,各年度專利申請具有多變性,采用灰色系統理論進行專利趨勢預測,可以剔除不可比因素,并且對預測所需的專利數據多少不限,建立的數學模型能夠滿足精度要求,預測結果更加可靠。
2.1 Logistic曲線計算
2.1.1 三等分計算方法
設時序列數據為y,t表示時序列號,則曲線公式
Y=k-ABt,
(1)
(2)

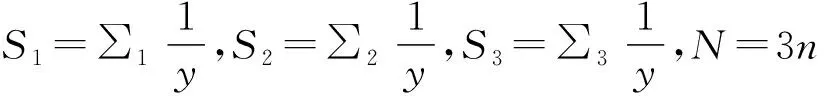
(3)
(4)
(5)
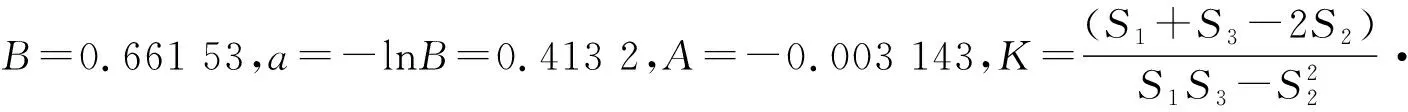
n=4 407.243,m=-A·K=13.851 96,則
(6)
2.1.2 利用SPSS擬合Logistic曲線方程
根據上述三等分計算方法測算估計K=4 400,運用社會科學統計軟件(Statistical Package for the Social Sciences,SPSS)[3]模擬原始序列數據y曲線,得
(7)
從軟件計算可知R2=0.981,其中R2是以回歸偏差占總偏差的比率來表示回歸模型擬合優度的評價指標,該處R2值表明模型對數據的擬合度非常好(以下均采用SPSS擬合的Logistic曲線進行預測)。中國軸承產業技術領域預測的專利申請見表4,表中數據均取整。原始序列數據y的Logistic回歸曲線如圖1所示。

圖1 中國軸承產業技術領域年度專利申請總量Logistic預測曲線
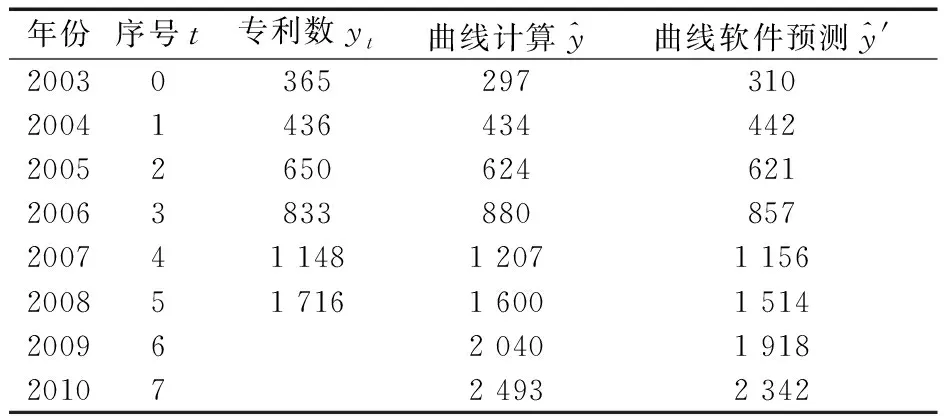
表4 中國軸承技術領域專利申請邏輯曲線計算預測表
同理,國內軸承企業技術領域年度專利申請預測Logistic曲線方程為
(8)
軟件計算得R2=0.963,表明模型對數據的擬合度較好。預測數據見表5,Logistic回歸曲線如圖2所示。

表5 國內專利申請人軸承技術領域專利申請邏輯曲線計算預測表

圖2 國內企業軸承技術領域專利申請Logistic預測曲線
同上,國外軸承企業在華技術領域專利申請預測Logistic曲線方程為
(9)
軟件計算得R2=0.975,表明模型對數據的擬合度較好。預測數據見表6,Logistic回歸曲線如圖3所示。
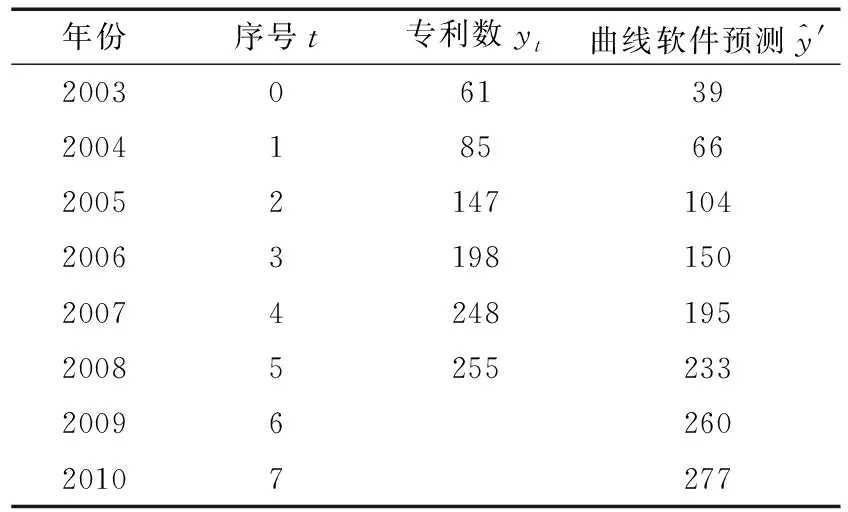
表6 國外專利申請人軸承技術領域專利申請邏輯曲線計算預測表

圖3 國外企業軸承技術領域專利申請Logistic預測曲線
2.2 灰色動態預測法模型構建
在專利技術趨勢預測中,采用灰色預測模型中的GM(1,1)模型。GM(1,1)模型是基于隨機的原始時間序列,經按照時間累加后形成新的時間序列所表現出的規律,其近似滿足微分方程條件。
設原始時間數據列X(0)={X(0)(1),X(0)(2),…,X(0)(n)},
(10)
對原始序列進行一次累加后,得到的新數據列
X(1)={X(1)(1),X(1)(2),…,X(1)(n)}
。(11)
則GM(1,1)模型相應的微分方程為
(12)
式中:α為發展灰數;μ為內生控制灰數。
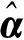
(13)
(14)
根據(10)~(14)式和表1的數據(選取2003—2008年的數據)可得:
X(0)=(365,436,650,833,1 148,1 716),
X(1)(365,801,1 451,2 284,3 432,5 148),
Y=(436,650,833,1 148,1 716)。

表7 中國軸承技術領域專利申請邏輯曲線計算預測表
同理,利用灰色動態預測模型計算得到國內企業軸承技術領域專利申請預測趨勢見表8,國外企業軸承技術領域專利申請預測趨勢見表9。
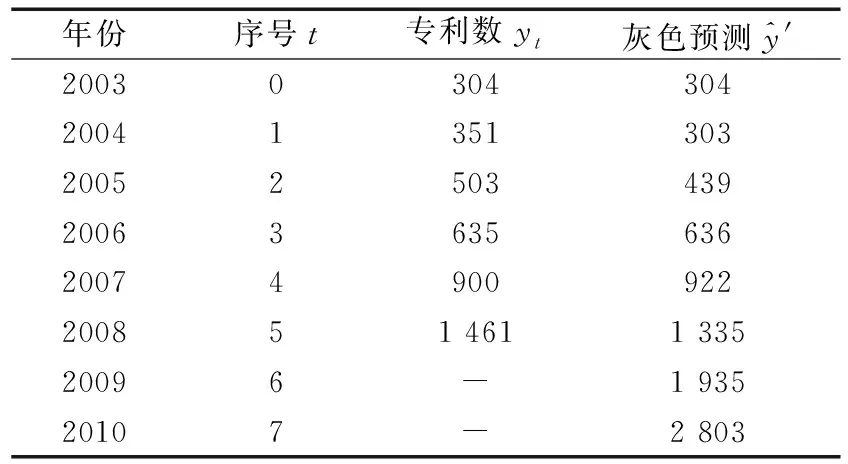
表8 國內專利申請人軸承技術領域專利申請灰色預測表
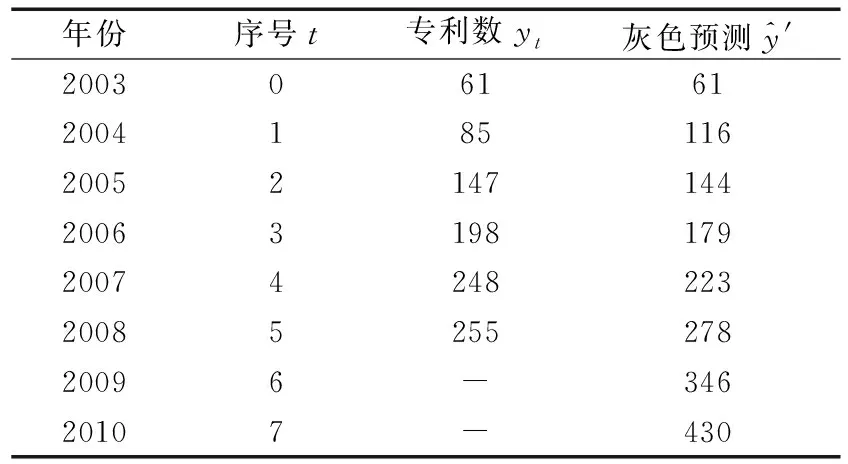
表9 國外專利申請人軸承技術領域專利申請灰色預測表
3 模型預測精度評價
根據上述計算得出的預測值,利用預測精度評價函數對以上2種數學模型進行精度評價(均以中國軸承技術領域預測結果為例)。
3.1 生長曲線Logistic數學模型
則有

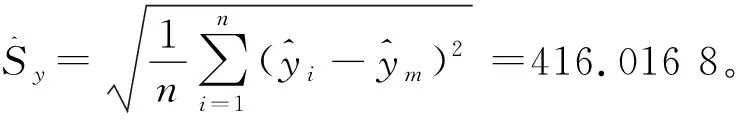

3.2 灰色動態GM(1,1)數學模型
則有
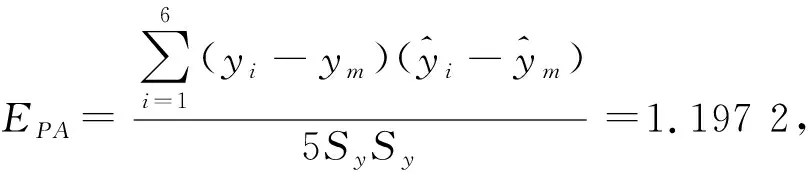
3.3 灰色模型檢驗
灰色動態模型使用方差比和常用的小誤差概率對模型進行檢驗。預測誤差
(15)
故有e(1)=0;e(2)=13;e(3)=57;e(4)=2;e(5)=17;e(6)=83。

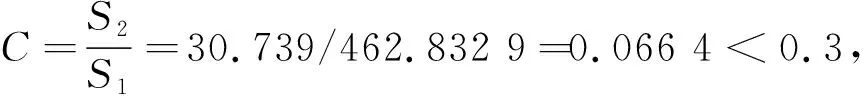
GM(1,1)模型精度等級見表10,精度等級越小越好,4級為不通過。由表可知,文中取得的模型精度符合1級,說明預測結果可靠性較高,即灰色動態預測模型的預測結果更為準確可靠。

表10 灰色動態GM(1,1)模型精度等級表
4 結束語
利用數學統計理論對中國軸承產業專利信息進行定量分析,通過時間序列生長曲線以及灰色動態數學模型的建立,對比計算分析了2種統計預測理論的精度,同時對灰色動態模型的可靠性進行了評價,進而有效預測了中國軸承產業未來2年的專利技術申請趨勢。結合以上2種預測方法,可以得出中國軸承技術領域2009年專利申請約為2 100件左右,2010年專利申請約為2 700件左右,其中,國外專利申請人軸承技術領域2009年專利申請約為300件左右,2010年專利申請約為350件左右。

