基于SG濾波器和組合窗STFT的滾動軸承故障診斷方法

王勇，鄧四二，王恒迪

(河南科技大學 機電工程學院，河南 洛陽 471003)

滾動軸承的振動信號往往表現為非平穩特征，當有局部損傷存在時，如何從非平穩的振動信號中提取出故障信息是滾動軸承故障診斷的關鍵問題。短時Fourier變換(short-time Fourier transform,STFT)是一種聯合時頻分析方法[1]，表征了非平穩信號頻率隨時間的變化關系，能夠得到信號在時域和頻域內的全貌和局部信息，是一種實用的非平穩信號故障診斷方法。然而由于傳統的STFT變換采用固定的窗函數[2]，無法同時滿足高的時間分辨率和頻率分辨率；而且目前自適應窗函數[3]的計算量較大，可靠性也有待進一步驗證。另外，振動信號中往往存在著較強的窄帶脈沖和隨機噪聲干擾，會嚴重影響STFT的分析精度，因此在STFT變換之前需要采用合適的方法對振動信號進行預處理。基于以上原因，提出了一種基于SG(Savitzky-Golay)濾波和組合窗STFT的滾動軸承故障診斷方法。該方法將SG濾波器[4-5]作為STFT的前置濾波單元，對信號濾波消噪后再利用長、短2個窗函數設計出一個新的組合窗[6]，利用組合窗提高STFT的時頻分辨率并應用于軸承振動信號分析。

1 基于SG濾波器的組合窗STFT

1.1 SG濾波器

SG濾波器是根據多項式最小平方擬合方法導出的濾波器，與傳統濾波器相比，其優點是形式簡單、計算量小、無需確定濾波器的截止頻率，能夠顯著地提高信噪比。其推導過程如下：

設一組數據為xi,i=-M，…，0，…，M，現構造一個p階多項式yi來擬合xi，

p≤2M。

(1)

總的擬合誤差為

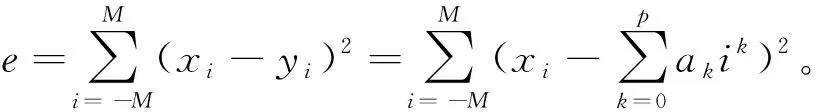
(2)

為了使擬合誤差e最小，令e對ar的偏導數為零，即

r=0，1，…，p，

(3)

整理(3)式可得

(4)

實際應用時(4)式取M=2，p=3即可滿足平滑濾波的要求，解出a0，a1，a2，a3代入(1)式，并令i=0，±1，±2,得到y-2，y-1，y0，y1，y2共5個點的表達式。由于yi最高階次為3，故此時的SG濾波器又可以稱為五點三次平滑法。當xi的點數較多時，xi的起始點分別用y-2和y-1表示，中間點均用y0表示，末尾2點分別用y1和y2表示。

;i=3,4,…,n-2。

(5)

需要注意的是，五點三次平滑法會使波形的峰值降低，造成擬合誤差增大，因此平滑次數不宜過多。

1.2 組合窗STFT

STFT是一種非線性信號分析方法，能夠同時提供時域和頻域的局部信息，在旋轉機械的振動分析中發揮了很大作用。STFT的基本思想是把信號劃分成許多小的時間間隔，然后用一個窗函數g(t-τ)對信號x(t)的乘積運算實現在τ附近的平移，再用Fourier變換分析每一個時間間隔，以確定時間間隔內存在的頻率成分。

信號x(t)的STFT定義為

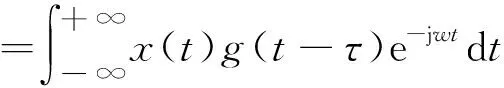
(6)

式中：g(t-τ)是中心為τ的窗函數，起時限作用；e-j2πft起頻限作用。分別令x(t)=δ(t-τ0)，x(t)=exp(jw0t)，得

STFTX(w,τ)=exp(-jwt0)g(t-t0)，

(7)

STFTX(w,τ)=exp[-j(w-w0)]g′(w-w0)。

(8)

(7)式和(8)式表明信號的STFT分析結果受窗函數的影響很大，高的時間分辨率需要較短的窗函數，而高的頻率分辨率需要較長的窗函數。由Heisenberg不確定原理可知，高的時間分辨率和頻率分辨率無法同時滿足。在進行STFT分析時，時頻窗不具有自適應性，無法自動改變其大小，窗函數一旦確定，則在整個分析過程中在時間-頻率平面上的所有局域分辨精度都是相同的，因此傳統STFT方法在分析軸承振動信號時，很難準確地提取出故障信息。

1.3 改進STFT

針對傳統STFT方法的不足，采用長、短窗函數相結合的方式對STFT進行改進，其原理如下：若信號能量分布在時間區間[-t,t]和頻率區間[-f,f]，則在區間[-t,t]×[-f,f]上進行STFT變換，信號能量基本不會泄漏。因此首先用SG濾波器得到降噪信號，然后選擇一個長窗函數和一個短窗函數分別對原始振動信號進行STFT變換，再把兩者相乘就實現了改進的STFT變換，具體實現過程如圖1所示。

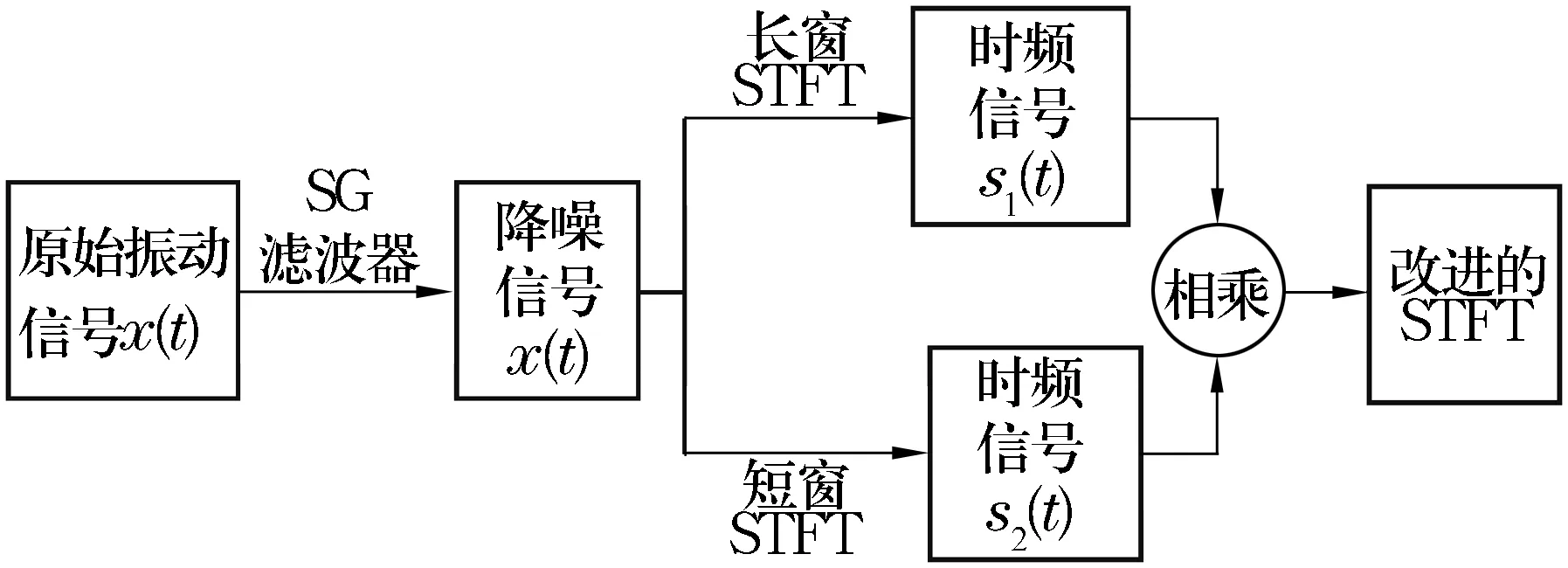
圖1 基于SG濾波器的組合窗STFT的實現過程

2 仿真分析

仿真信號x(t)的時域波形如圖2a所示，其由3個受到白噪聲干擾的正弦信號組成，正弦信號的頻率分別為100，200和300 Hz，幅值依次降低。圖2b是采用1/2數據長度的Hanning窗對x(t)直接進行STFT變換求得的時頻圖譜，從圖中可以看出，由于受到了白噪聲的干擾，正弦信號的3個頻率成分很難被識別出來。圖2c是用SG濾波器對圖2b所示的時頻圖譜進行降噪處理后的結果。從圖中可以看出，白噪聲的影響大大降低，3個頻率成分已經被識別出來，然而譜線較為模糊，300 Hz的頻率成分幾乎看不到。圖2d是用圖1所示方法，先用SG濾波器對振動信號降噪，然后用1/2數據長度的Hanning窗和1/8數據長度的Hanning窗得到組合窗對x(t)進行STFT變換求得的時頻圖譜，從圖中可以清晰地看到100，200，300 Hz的頻率成分，與圖2c相比，大大提高了時頻分辨率。

圖2 仿真信號的時頻分析方法對比

仿真分析的結果表明，與傳統的固定窗STFT變換相比，基于SG濾波器的組合窗STFT不僅可以抑制隨機噪聲的干擾，而且能夠獲得更高的時頻分辨率，提高了STFT變換的精度。

3 試驗驗證

試驗軸承型號為6203和6012，其中6203的內徑為17 mm，外徑為40 mm，鋼球直徑為6.747 mm，鋼球個數為8；6012的內徑為60 mm，外徑為110 mm，鋼球直徑為15.08 mm，鋼球個數為10。根據6203和6012的基本參數求得的理論故障頻率見表1。

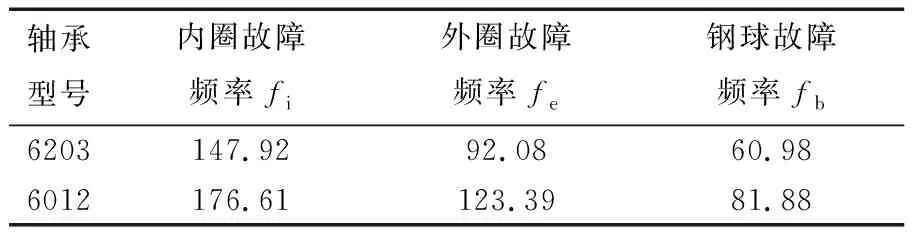
表1 6203和6012的理論故障頻率 Hz

軸承振動信號的采樣頻率為40 000 Hz，采樣點數為5 000。下面是測振儀上得到的2種典型振動信號的分析結果。

圖3a是6203外圈損傷振動速度信號，圖3b是采用長度為1/4的Hanning窗進行STFT變換求得的時頻譜，圖3c是用組合窗法得到的時頻分布圖(組合窗是一個1/4數據長度的Hanning窗和長度為1/16的Hanning窗)。對比圖3b和圖3c可見，改進的STFT譜線更加清晰，明顯提高了時頻分辨率，比傳統方法更為準確。從圖3c可以清晰地看到2條譜線的時間間隔ΔT約為0.011 s，即軸承的故障頻率為1/ΔT=90.9 Hz，與6203的理論故障頻率對比可知該故障頻率與外圈故障頻率(92.08 Hz)較接近，因此可以判斷該軸承的故障部位在外圈上。

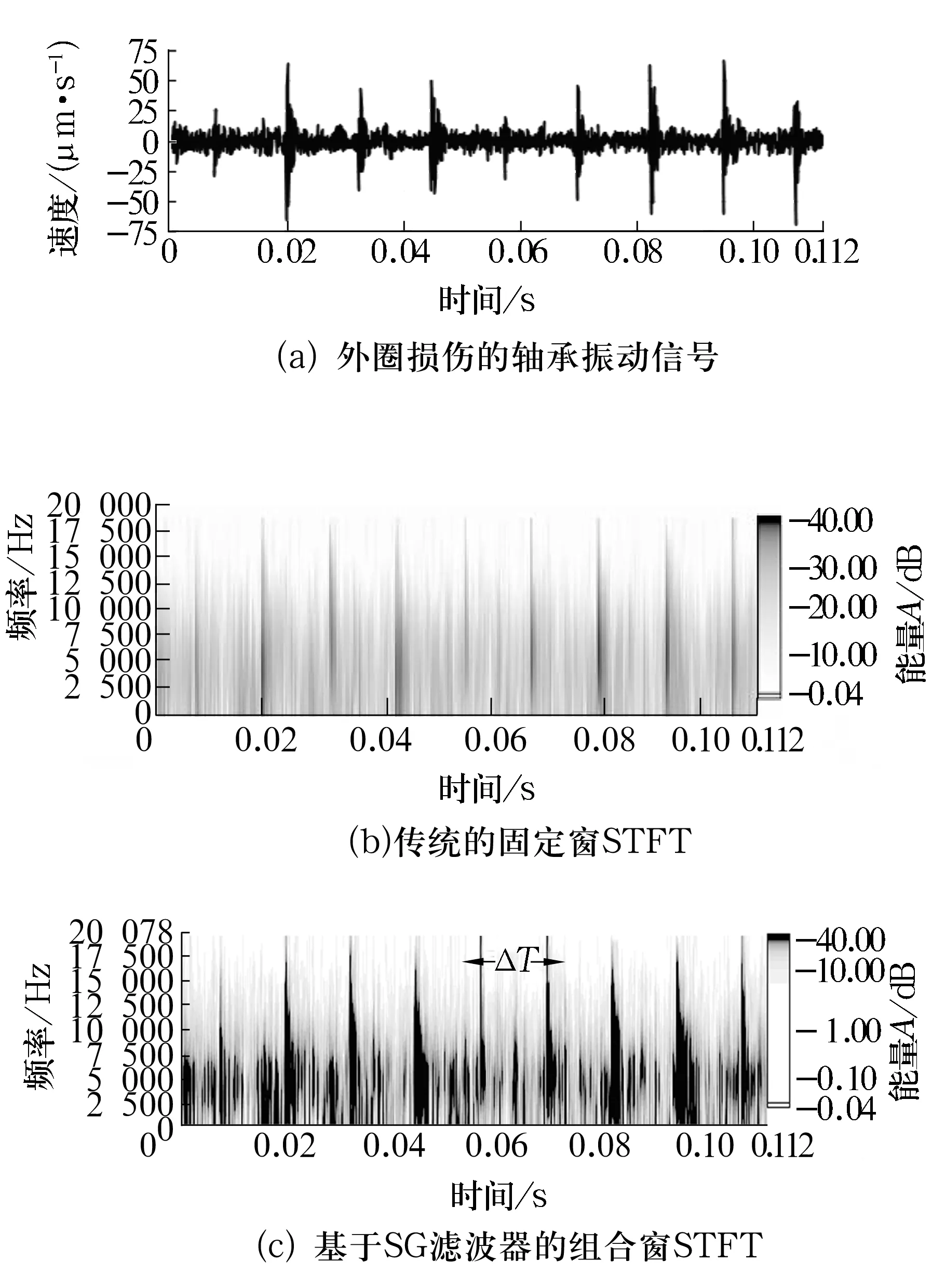
圖3 6203外圈損傷的時頻分析方法對比

圖4a是6012外圈有輕微損傷的振動速度信號，圖4b是采用1/4數據長度的Hanning窗進行STFT變換求得的時頻譜，圖4c是用基于SG濾波器的組合窗STFT求得的時頻分布圖，其中組合窗是一個1/4數據長度的Hanning窗和一個1/16數據長度的Hanning窗。對比圖4b和圖4c可知，傳統的固定窗函數STFT診斷效果較差，而組合窗STFT明顯提高了時頻分辨率，更易發現軸承故障。從圖4c可以清晰地看到2條譜線的時間間隔ΔT約為0.008 s，即軸承的故障頻率為1/ΔT=125 Hz，和6012的理論故障頻率對比可知該故障頻率與外圈故障頻率(123.39 Hz)較接近，因此可以判斷該軸承的故障部位發生在外圈上。

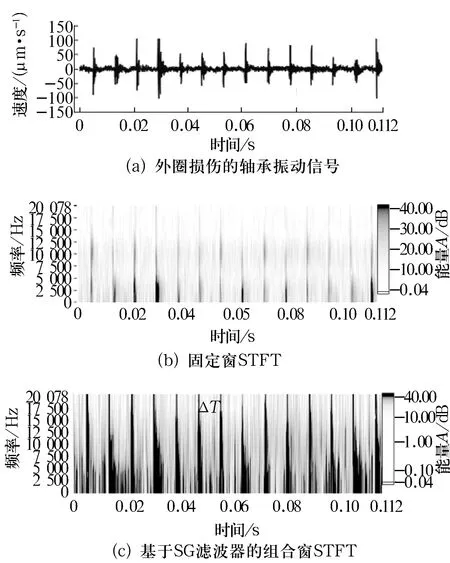
圖4 6012外圈損傷的時頻分析方法對比

4 結束語

提出了一種基于SG濾波的組合窗STFT的滾動軸承故障診斷方法，將SG濾波器用于振動信號去噪，采用長、短窗函數獲得2組STFT時頻表示并以乘積結果作為最終時頻表示的組合窗。數值仿真和軸承故障診斷實例的結果表明，該方法能更加有效地增大信噪比，與傳統的固定窗函數相比，組合窗STFT變換的時頻聚集性得到了很大提高，突出了故障振動信號的故障特征，提高了故障診斷的準確性。