廣東西江北江洪水聯合概率分布研究*
陳子燊,劉曾美,路劍飛
(1. 中山大學水資源與環境系,廣東 廣州510275;2. 華南理工大學水利水電工程系,廣東 廣州510640)
1 研究背景
多變量極端事件之間的相關性普遍存在于水文氣象領域。然而,至今對于極端水文氣象事件的概率分布研究多數還是基于單變量的統計分析。一些研究嘗試利用多變量正態聯合分布,但由于要求邊緣分布必須是正態或對數正態分布,因此限制了模型使用和選擇范圍。近些年來借助于Copula函數,多變量聯合分布已經在水文氣象極值事件分析中得到了較深入的研究[1-9],為更精確地推算極端事件的重現水平和控制工程風險提供了一個重要的理論基礎和技術手段。
流入廣東省的西江發源于云南省霑益縣馬雄山,至廣西梧州會桂江后始稱西江,東流至三水市思賢滘與北江相通。北江發源于江西省信豐縣石碣大茅坑,流入韶關市與武江匯合后始稱北江,此后向南流經清遠市,經思賢滘與西江干流連通后進入珠江三角洲網河區。位于珠江三角洲西北部頂點思賢滘兩側的馬口站和三水站屬于國家重點水文觀測站,分別監測進入西北江三角洲網河區的流量過程。20世紀80年代以來,珠江三角洲經濟和城市化進程高速發展,三角洲出現了大規模無序的河道采沙,河道發生了大規模的下切,而三水測站所處的河道斷面下切幅度遠遠大于同期馬口測站所在的河道斷面下切幅度。由于思賢滘的連通作用,造成三水斷面的水量分配比不斷增大[10 ]。西北江洪水受流域特征制約,兩江洪水特性差異明顯。每年洪水發生時間通常北江早于西江,兩江同時發洪的情況也時有發生[11]。通過馬口、三水的兩江洪水直接威脅珠江西北江三角洲的防洪安全,深入分析兩江洪水遭遇的聯合概率分布特征對于防御西、北江洪水拱衛廣州等珠三角城市的飛來峽水利工程樞紐的洪水調度和洪水資源的規劃利用具有重要意義。
2 基于Copula函數的聯合概率分布模型
2.1 Copula函數、參數估計和擬合優度評價
根據Sklar定理,令F是具有單變量邊緣分布函數F1,...,Fn的n維分布函數,若邊緣分布函數F1,...,Fn連續,則存在一個唯一滿足F(x1,...,xn)=C(F1(x1),...,Fn(xn))關系的連接函數C。相反,如果C是一個n維Copula,F1,...,Fn為分布函數。作為一新的統計方法,Copula函數為描述隨機變量之間的相關結構提供了一個新思路而得到了廣泛應用。利用Copula函數建立多變量的聯合分布的突出優點是:① Copula函數能夠把邊緣分布和變量間的相關關系分開處理,因此能夠對邊緣分布靈活選擇,選擇能較好地刻畫單變量自身的變化規律的邊緣分布;② Copula函數能夠捕捉隨機變量間的非線性相關關系, 且求解比較簡單,相對于線性相關提高了適用范圍;③ 由Copula函數導出的一系列的相關性度量指標,拓展了變量間的相關性度量范圍,在實際工作中有更加廣泛的應用。Nelsen[12]系統地總結了Copula函數的性質和這個領域的主要研究成果。郭生練等較全面地介紹了Copula 函數在水文分析計算中的應用[13]。
根據Copula函數性質,構建兩變量間的聯合概率分布模型可分兩步進行:首先確定邊緣分布,然后選擇一個能夠恰當地反映變量間的相關結構的Copula函數。研究表明,阿基米德(Archimedean)Copula是由其生成元唯一確定的單參數函數,是當前應用于水文氣象領域的一類非常重要的Copula函數。幾種常用二維Archimedean Copula函數為:
① Gumbel-Hougaard(GH) Copula函數:
C(u,v)=exp{-[(-lnu)θ+(-lnv)θ]1/θ},
θ∈[1,∞)
(1)
其生成元φ(t)為:φ(t)=(-lnt)θ。GHCopula函數僅適用于變量存在正相關的情形。
②Clayton Copula函數:
C(u,v)=(u-θ+v-θ-1)-1/θ,
θ∈(0,∞)
(2)
其生成元φ(t)為:φ(t)=(t-θ-1)/θ。同GH函數,適用于描述正相關的隨機變量。
③Ali-Mikhail-Haq (AMH)Copula函數:
C(u,v)=uv/[1-θ(1-u)(1-v)],
θ∈[-1,1)
(3)
其生成元φ(t)為:φ(t)=ln(1-θ(1-t)/t)。AMH函數能夠描述正或負相關的隨機變量,但不適用于正相關或負相關非常高的變量。
④Frank Copula函數:
C(u,v)=-ln{1+[(e-θu-1)(e-θv-1)/
(e-θ-1)]}/θ,θ∈R
(4)
其生成元φ(t)為:φ(t)=-ln[(e-θt-1)/(e-θ-1)]。與AMH Copula函數類似,但對相關程度沒有限制。
由于使用不同的Copula函數分析結果可能明顯不同,因此對Copula 函數的擬合優度檢驗以選擇合適的Copula函數顯得十分重要。擇優選用Copula函數的主要檢驗方法有由圖示直觀選擇Copula 函數的Genest-Rivest方法[14]、均方根誤差(RMSE)準則法和AIC 信息準則法等。
2.2 概率分布與重現期
根據Copula函數,兩變量聯合分布可表示為:
1999年11月,國家經貿委與世界銀行召開“現代物流發展國際研討會”。時任國務院副總理吳邦國提出,“要把現代物流作為國民經濟的重要產業和國民經濟新的增長點。”
F(x,y)=P(X≤x,Y≤y)=
C(FX(x),FY(y))
(5)
變量X和Y的邊緣分布重現期:
(6)
變量X、Y的聯合重現期To:
(7)
變量X和的Y同現重現期Ta:
(8)
由以上可得:To(x,y)≤Min(T(x),T(y))≤Max(T(x),T(y))≤Ta(x,y)
當給定X≥x時,Y≥y的條件概率:
(9)
同理,可定義Y≥y時,X≥x的概率。由條件概率分布,可計算相應的條件重現期。
3 西北江洪水聯合概率分布
3.1 洪峰流量數據
基本資料為1959-2007年間馬口、三水兩測站的日平均流量。兩江洪水聯合概率分布分析所用的樣本分別以馬口歷年最大日均洪峰流量和同步的三水洪峰流量、三水歷年最大日均洪峰流量和同步的馬口洪峰流量兩組抽樣數據構成,即:馬口-三水洪水(樣本1)、三水-馬口洪水(樣本2)。
3.2 聯合分布計算與分析
3.2.1 邊緣分布 函數對兩樣本的邊緣分布,都使用了以下3個三參數的概率分布函數擇優:
1)廣義極值分布(GEV):
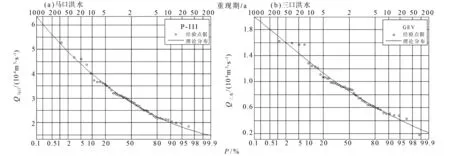
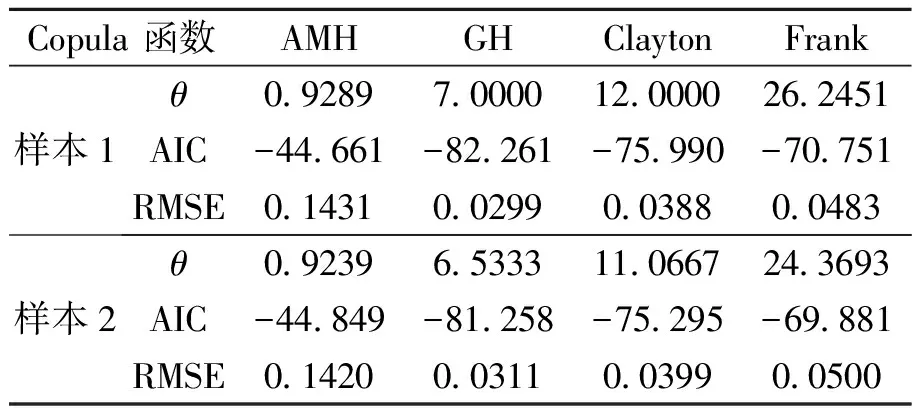
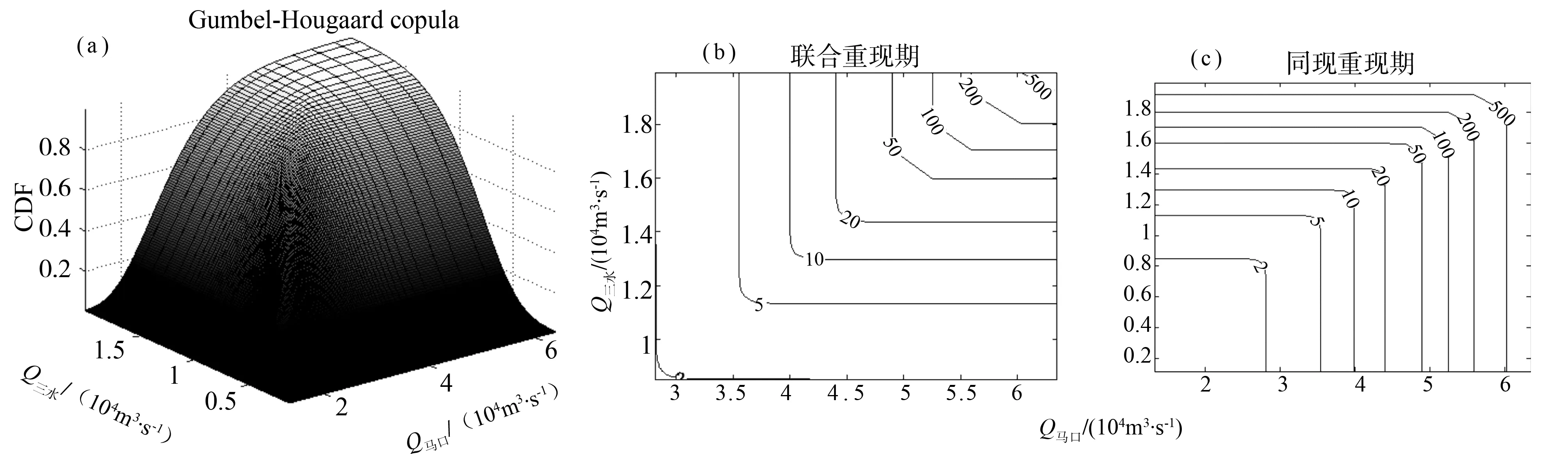
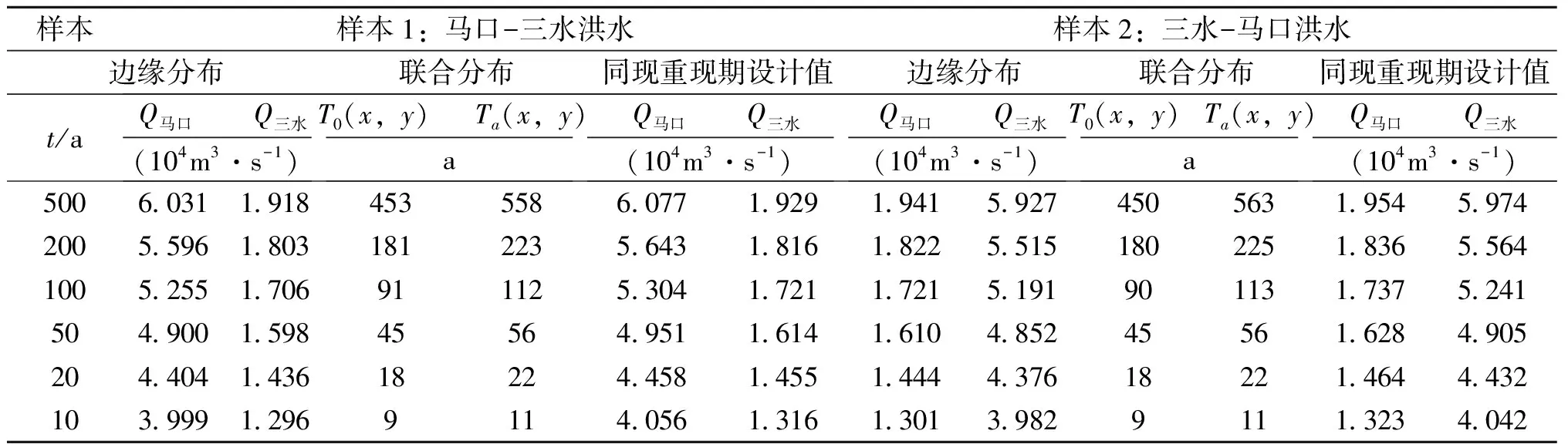
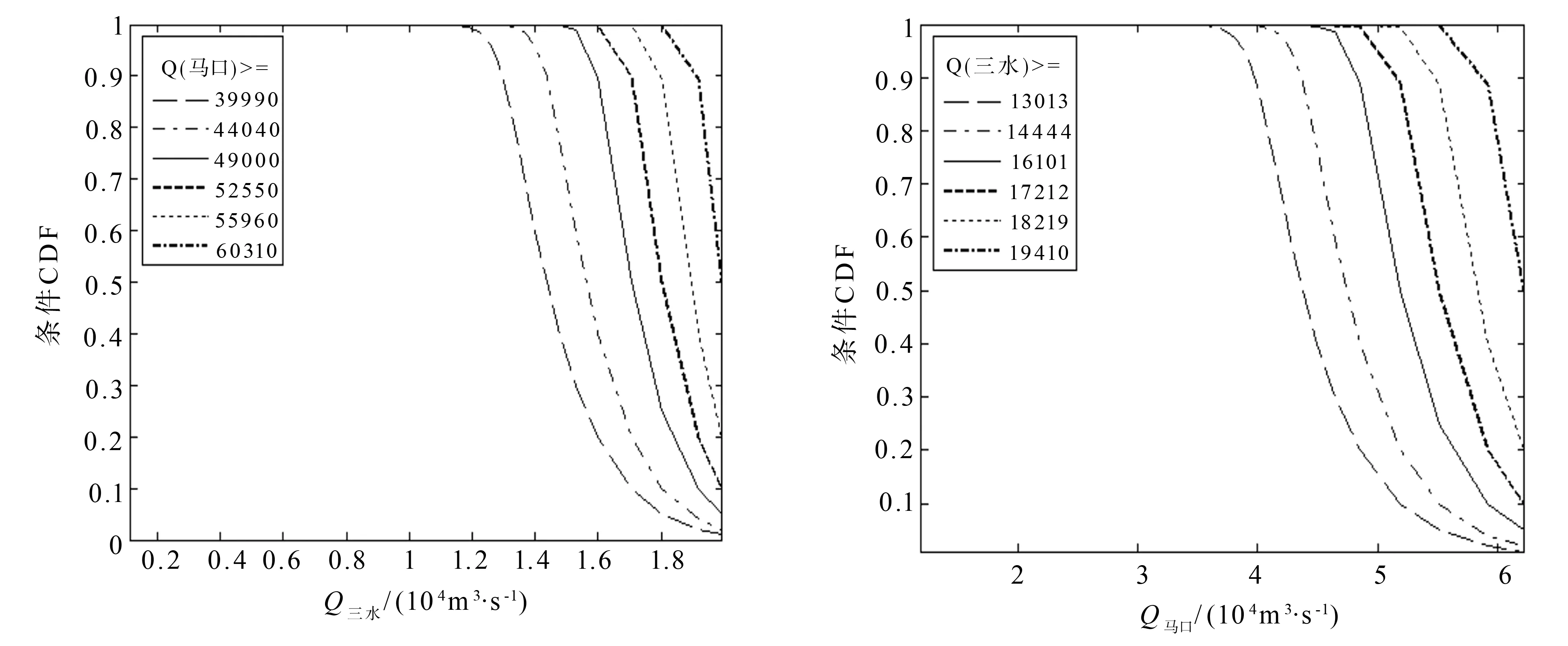
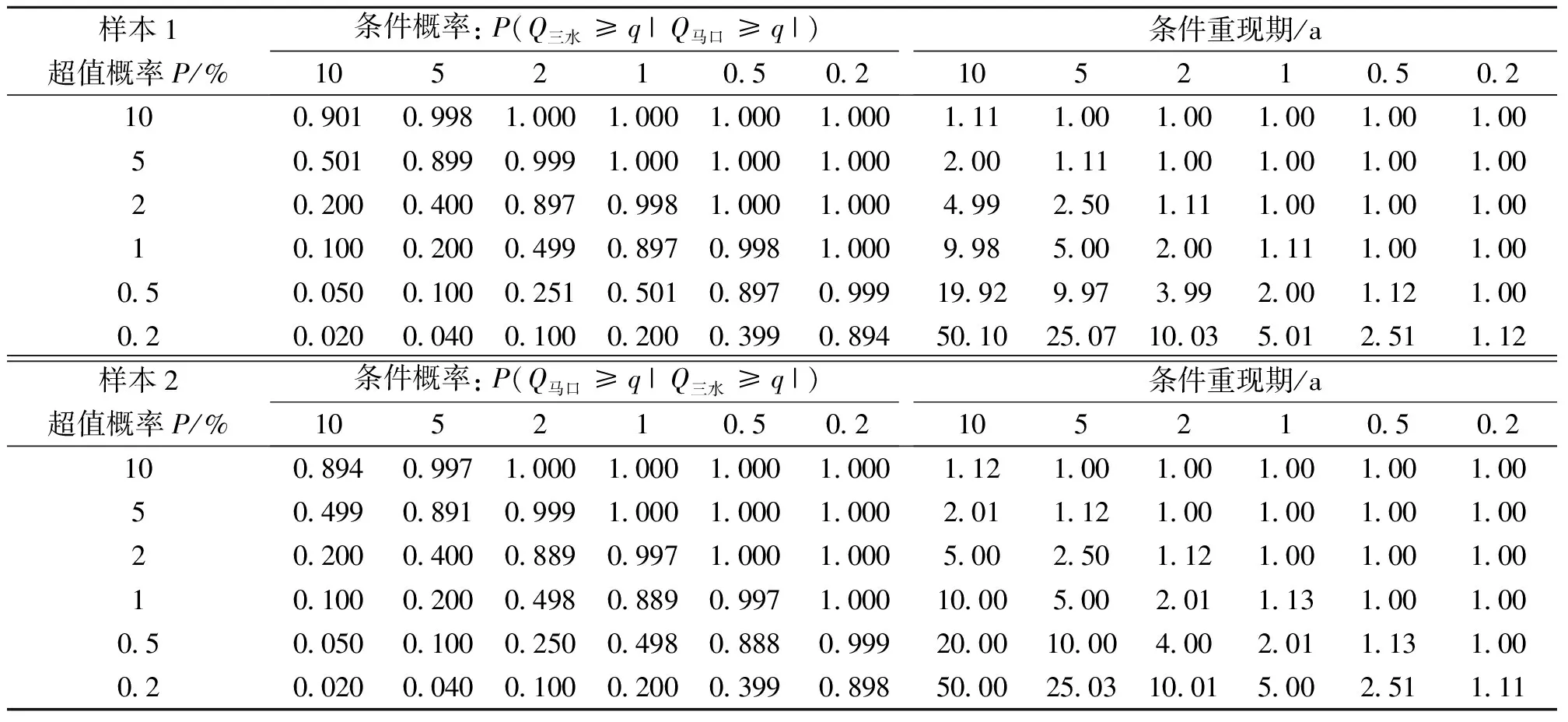
FX(x)=P(X (10) 2)皮爾遜三型分布(P-III): FX(x)=P(X (11) 3)威布爾分布(WBL): FX(x)=P(X (12) 式中,ξ,β,μ,α,a0為分布函數參數。參數估計使用概率權重矩(PWM)或線性矩(L-矩)方法。經驗頻率分布Pi使用Gringorten公式計算:Pi=(i-0.44)/(n+0.12)。擬合結果采用均方根誤差(RMSE)、經驗頻率和理論頻率擬合誤差平方和(Q)和概率點據相關系數(PPCC)檢驗其擬合優度。根據優度檢驗結果(表1)綜合比較,兩樣本的馬口和三水較優邊緣分布分別選用P-III分布和GEV分布(圖1)。樣本2的邊緣分布線型和擬合優度檢驗結果基本同樣本1,為省去篇幅不再列出圖與表。 3.2.2 Copula 函數的參數估計及擬合優度評價 由Kendall秩相關系數(τ)計算的馬口、三水洪水之間相關性分別為,樣本1:τ=0.857;τ=0.847。采用相關性指標法計算了兩個聯合概率分布樣本的copula參數θ,并利用AIC、RMSE檢驗其擬合優度,結果見表2。根據擬合優度評價指標,選擇兩樣本中AIC和RMSE最小、KT-Ke關系圖中點據和理論直線最接近45°對角線的GH Copu1a函數作為聯合概率分布的連接函數(圖略)。GH Copu1a函數的θ=7.0(明顯大于1),反映兩站洪水聯合概率分布之間存在很高的上尾相關性,即,當其中一個測站洪水出現小頻率的洪峰流量時,另一個測站洪水出現小頻率的洪峰流量的概率隨之增大,此對于進一步深入分析兩測站洪水的空間相關性和聯合概率分布特征提供了重要的基礎。擇優構建馬口、三水洪水聯合概率分布的GH Copula聯合分布函數如下: 表1 樣本1的邊緣分布參數與優度檢驗值 圖1 樣本1馬口洪水和三水洪水兩變量邊緣分布圖 樣本1:C1(FX(x),FY(y))=exp{- [(-lnFX(x))7.00+(-lnFY(y))7.00]1/7.00} (13) 樣本2:C2(FX(x),FY(y))=exp{- [(-lnFX(x))6.53+(-lnFY(y))6.53]1/6.53} (14) 表2 兩樣本的Copula參數及擬合優度評價指標 3.2.3 聯合概率分布與重現期 樣本1的聯合分布、聯合重現期和同現重現期見圖2所示(樣本2的聯合概率分布與重現期圖與圖2基本相同,為省篇幅略去)不同重現期的洪水設計值見表3。 表3顯示,聯合重現期小于邊緣分布重現期,邊緣分布重現期則小于同現重現期。根據單變量同頻率方法推算的設計值小于兩站洪水聯合重現期設計值,差值隨重現期減小而有所增大,馬口洪水設計值相對差值大約介于0.8%~1.4%,三水洪水設計值相對差值大約介于0.6%~1.5%。受樣本抽樣方法影響,使得同頻率條件下樣本1的馬口洪水設計值略大于樣本2的設計值,樣本1的三水洪水設計值則略小于樣本2的設計值。在設計頻率的低頻部分,樣本2的同現重現期略大于樣本1的同現重現期。以200 a一遇洪水為例,樣本1中馬口、三水邊緣分布重現期設計值分別為55 960和18 790.m3/s,同頻率的聯合分布重現期設計值分別為564 310.和18 960.m3/s;樣本2中馬口、三水邊緣分布重現期設計值分別為55 150和18 220.m3/s,聯合分布重現期設計值分別為55 640和18 360.m3/s;樣本1邊緣分布200 a一遇的同現重現期為223年,樣本1邊緣分布200 a一遇的同現重現期為225 a。上述結果表明,與兩江洪水遭遇聯合概率分布比較,以單變量推算的馬口、三水洪水設計值實際上沒有達到設計標準。 3.2.4 條件概率分布 考慮到西江和北江流域爆發洪水的時間差異,需要進一步分析馬口(三水)洪水出現某特定流量條件下,三水(馬口)洪水流量的概率分布。圖3表示當馬口出現10%、5%、2%、1%、0.5%和0.2%超值概率的洪水時,三水遭遇洪水超過相應標準洪水的條件概率P(Q三水≥q|Q馬口≥q|)。圖4表示當三水出現超值概率為10%、5%、2%、1%、0.5%和0.2%洪水時,馬口遭遇的洪水超過相應標準洪水的條件概率P(Q馬口≥q|Q三水≥q|)。表4說明,當馬口(三水)洪水大于等于某一特定頻率設計值時,三水(馬口)出現大于等于該頻率設計值的條件概率隨著超值概率的減小而減小,以馬口出現大于等于概率P10%時的洪水為例,三水洪水出現大于等于概率P10%、P5%、P2%、P1%、P0.5%和P0.2%的條件概率分別為0.901、0.501、0.200、0.100、0.050和0.020,其相應的條件重現期為:1.11、2、4.99、9.98、19.92和50.1。兩站相同設計頻率洪水相遇的概率都超過88%,充分表明馬口與三水洪水之間關系密切,同頻率洪水之間遭遇的概率非常高,由馬口或三水洪水設計值大致可推算出同頻率的三水或馬口洪水設計值。 圖2 樣本1聯合分布三維圖、聯合重現期等值線圖、同現重現期等值線圖 表3 馬口、三水洪水不同重現期的洪水設計值 Table 3 Flood design values for different return periods of Makou and Sanshui Stations 樣本樣本1:馬口-三水洪水樣本2:三水-馬口洪水邊緣分布聯合分布同現重現期設計值邊緣分布聯合分布同現重現期設計值t/aQ馬口 Q三水(104m3·s-1)T0(x,y) Ta(x,y)aQ馬口 Q三水(104m3·s-1)Q馬口 Q三水(104m3·s-1)T0(x,y)Ta(x,y)aQ馬口 Q三水(104m3·s-1)5006.0311.9184535586.0771.9291.9415.9274505631.9545.9742005.5961.8031812235.6431.8161.8225.5151802251.8365.5641005.2551.706911125.3041.7211.7215.191901131.7375.241504.9001.59845564.9511.6141.6104.85245561.6284.905204.4041.43618224.4581.4551.4444.37618221.4644.432103.9991.2969114.0561.3161.3013.9829111.3234.042 圖3 P(Q三水≥q|Q馬口≥q|)的條件概率分布圖 圖4 P(Q馬口≥q|Q三水≥q|)的條件概率分布圖 表4 兩站洪水遭遇條件概率 Table 4 Conditional probabilities of two station floods 樣本1超值概率P/%條件概率:P(Q三水≥q|Q馬口≥q|)105210.50.2條件重現期/a105210.50.2100.9010.9981.0001.0001.0001.0001.111.001.001.001.001.0050.5010.8990.9991.0001.0001.0002.001.111.001.001.001.0020.2000.4000.8970.9981.0001.0004.992.501.111.001.001.0010.1000.2000.4990.8970.9981.0009.985.002.001.111.001.000.50.0500.1000.2510.5010.8970.99919.929.973.992.001.121.000.20.0200.0400.1000.2000.3990.89450.1025.0710.035.012.511.12樣本2超值概率P/%條件概率:P(Q馬口≥q|Q三水≥q|)105210.50.2條件重現期/a105210.50.2100.8940.9971.0001.0001.0001.0001.121.001.001.001.001.0050.4990.8910.9991.0001.0001.0002.011.121.001.001.001.0020.2000.4000.8890.9971.0001.0005.002.501.121.001.001.0010.1000.2000.4980.8890.9971.00010.005.002.011.131.001.000.50.0500.1000.2500.4980.8880.99920.0010.004.002.011.131.000.20.0200.0400.1000.2000.3990.89850.0025.0310.015.002.511.11 利用由思賢滘相通的西江馬口和北江三水兩測站流量資料,本文分析了廣東西江與北江洪水之間的聯合概率分布特征,研究表明:兩站洪水之間存在高關聯性。基于Copula函數方法能夠選擇更優的邊緣分布,構造的聯合概率分布和條件概率更全面地反映了馬口和三水洪水極值統計特征和兩江洪水遭遇概率,為珠江西北江三角洲的防洪規劃與風險控制提出了一個較好的解決方案。 參考文獻: [1]閆寶偉,郭生練,肖義,等. 基于兩變量聯合分布的干旱特征分析[J]. 干旱區研究, 2007, 24(4): 537- 542 [2]方彬,郭生練,肖義,等. 年最大洪水兩變量聯合分布研究[J].水科學進展,2008, 19( 4):505-511 [3]陸桂華,閆桂霞,吳志勇,等.基于copula函數的區域干旱分析方法[J].水科學進展,2010,21(2):188-193 [4]劉曾美,陳子燊.區間暴雨和外江洪水位遭遇組合的風險[J]. 水科學進展,2009, 20(5): 619- 625. [5]ZHANG L, SINGH V P. Bivariate flood frequency analysis using the copula method [J]. Journal of Hydrologic Engineering, 2006, 11(2):150- 164. [6]ZHANG L, SINGH V P. Bivariate rainfall frequency distributions using Archimedean copulas [J]. Journal of Hydrology, 2007, 332:93- 109. [7]SHIAU J T, SONG F, NADARAJAH S. Assessment of hydrological droughts for the Yellow River, China, using copulas [J].Hydrological Processes, 2007, 21: 2157-2163. [8]FAVRE A C, ADLOUNI S E, PERRAULT L, et al. Multivariate hydrological frequency analysis using Copulas [J].Water Resources Research, 2004, 40(11):1-12. [9]JOE H. Multivariate Models and Dependence Concepts [M]. London:Chapman & Hall, 1997. [10]童娟.珠江流域概況及水文特性分析[J].水利科技與經濟,2007,13(1):31-33 [11]姚章民,王永勇,李愛鳴. 珠江三角洲主要河道水量分配比變化初步分析[J]. 人民珠江,2009(2):43-45, [12]NELSEN R B. An Introduction to Copulas. Springer Series in Statistics [M]. NewYork: Springer,1999:216 [13]郭生練,閆寶偉,肖義,等.Copula 函數在多變量水文分析計算中的應用及研究進展[J].水文,2008,28(3):1-7. [14]GENEST C, RIVEST L. Statistical inference procedures for bivariate Archimedean copulas [J]. Journal of American Statistical Association, 1993, 88: 1034- 1043.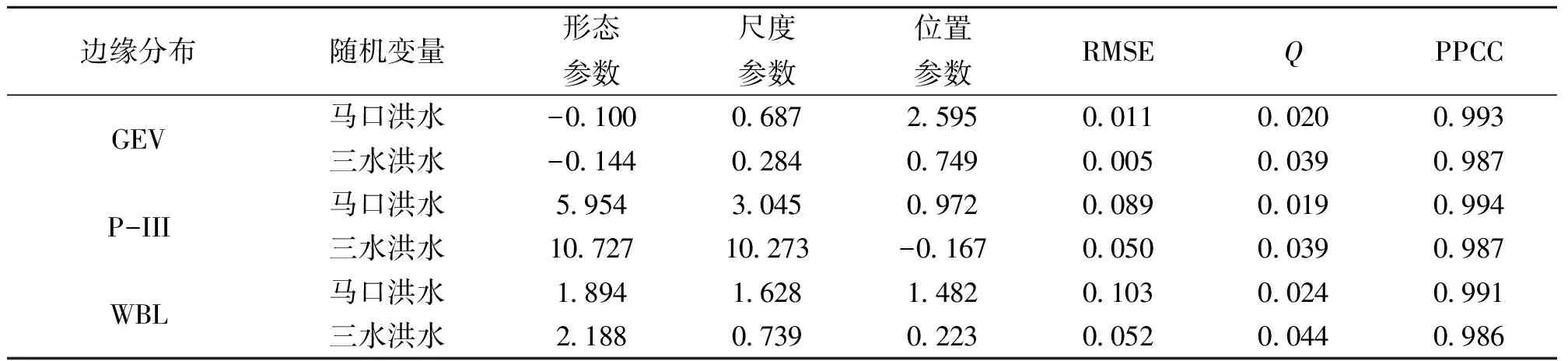
4 結 語

