“殊途不同歸”,原因何在?

鄭曙輝

(浙江省寧波第二中學,浙江寧波 315010)

2010年山東調研卷中有一道考題,該題考查運動學知識,同時考查運用數學知識處理物理問題的能力,情景新穎,運動模式既非勻速運動又非勻變速運動,是加速度隨時間均勻減小的變加速運動,但求解的方法又在學生掌握的能力范圍內.筆者把它作為一道習題布置給學生,結果引發學生的大爭論,原因是采用兩種不同方法做的學生都認為自己的解法完全正確,但結果卻并不相同,而且這個差異也不在計算的誤差范圍內,可謂“殊途不同歸”.原因何在?難道是其中一種方法有錯誤?筆者抓住這個契機,引導學生進行分析,查找原因所在,使學生通過爭議,獲取進步.

原題摘錄如下:

圖1

F1是英文Formula One的縮寫,即一級方程式賽車,是僅次于奧運會和世界杯的世界第三大賽事.F1賽車的變速系統非常強勁,從時速0加速到100 km/h僅需2.3 s,此時加速度仍達10 m/s2,時速為200 km/h時的加速度仍有3 m/s2,從 0加速到 200 km/h再急停到 0只需 12 s.假定F1賽車加速時的加速度隨時間的增大而均勻減小,急停時的加速度大小恒為9.2 m/s2.上海F1賽道全長5.451 km,比賽要求選手跑完56圈決出勝負.求:

(1)若某車手駕駛該賽車比賽時的平均速度為 210 km/h,則跑完全程用多長時間?

(2)該車手的F1賽車的最大加速度.

分析與解答:

該小題考查路程與平均速率的關系式,直接套用公式就可輕易求得答案,學生不會產生爭議.爭議的出現產生在第(2)小題中,下面對第2小題采用不同的方法進行解答.

方法1:聯立方程組求解.

(2)F1賽車加速時的加速度隨時間的增大而均勻減小,由題意可得:a=am-kt,其中am為賽車的最大加速度.

設賽車速度從200 km/h急停到零時,用時為t0,由運動學公式可得

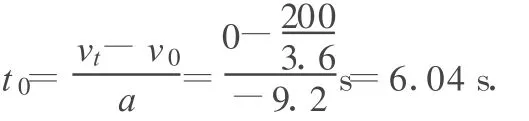
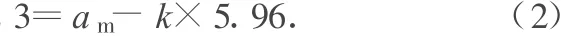
am=14.4 m/s2.

方法2:用a-t圖像法求解

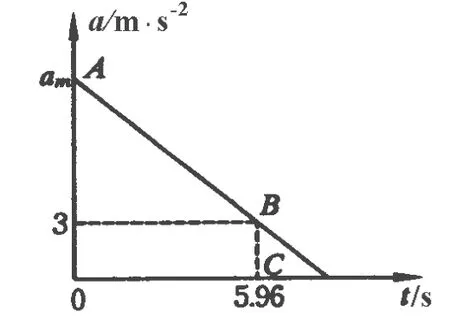
圖2

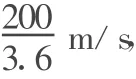
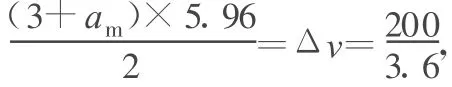
解得am=15.64 m/s2.

兩種不同的方法,得到的結果相差了1.24 m/s2,這絕對不是計算誤差所能簡單解釋的,引導學生對兩種求解方法的每一步進行仔細推敲,發現方法都正確!問題究竟出在哪里?為了引發學生積極思考,筆者又提出了一種新的解法,開拓學生的思路.

方法3:等效平均加速度法求解.

(2)設賽車速度從200 km/h急停到零時,用時為 t0,由運動學公式可得

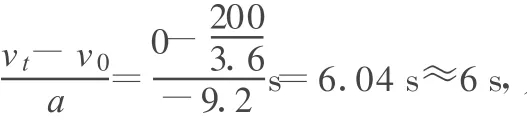
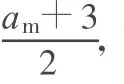
又一個不同的答案!

對方法3的答案和方法2的答案及其解答過程進行對照,容易發現,這兩個答案其實在計算誤差范圍內,略有差異主要是在時間的計算上進行了近似處理,如果把方法2的時間與方法3的時間進行同樣的處理,這兩個答案是非常接近的,在計算誤差范圍內可以近似看做相等.這樣,答案就傾向于am=15.4 m/s2了.

上述3種求解方法的思路各異,途徑各不相同,但方法正確.方法1和后兩種方法的答案為何會出現較大的偏差?再仔細分析這3種解法,發現后兩種都沒有用到時間在2.3 s時加速度達10 m/s2這一組數據,而方法1是采用時間在2.3 s時,加速度達10 m/s2和時間在5.96 s(或近似為6 s)時,加速度為3 m/s2時建立兩個方程解得.可見造成答案偏差的問題就出在當時間為2.3 s時,加速度達10 m/s2這一組數據不精確,2.3 s,10 m/s2不在 a-t圖線上.因此,筆者建議把該題的“從時速0加速到100 km/h速度仍達 10 m/s”,改為“從時速0加速到100 km/h僅需2.6 s,此時加速度仍達 10 m/s2”.依此條件建立的兩個方程組為

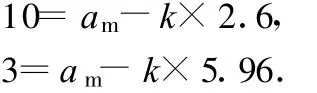
解得am=15.42 m/s2.這樣,3種方法求得的結果便一致了.

一個數據的瑕疵影響了整道題目的質量.這道題目的求解告誡我們,出題者除了把握科學性、知識性以外,對題目中所涉及到的每一個數據也要進行推敲,以免出現不應有的錯誤.教師在講解具體題目過程中,如果碰到了這種情況,更要抓住教學契機,引導學生進行正確、有效的討論,這樣“殊途”才能“同歸”,而不能隨意以題目有誤應付了事.這樣做的目的,除了對知識的尊重以外,更重要的是在對學生激發學習興趣的同時,也培養了學生嚴謹的科學態度,這比掌握一道習題的求解更為重要!