轉換情景性質求解物理問題

黃國超

(浙江諸暨草塔中學,浙江諸暨 311812)

“素質教育”要求注重培養學生解決實際問題的能力,而實際問題的相關信息往往不能和物理規律直接對接,這是學生在學習中的最大障礙之一,因此需要學生會建立合理的、最佳的物理情境,巧妙地解決實際問題.下面以幾個求時間的具體實例來說明轉換設計新的物理情境的重要性.這里“新”物理情景在性質上不同于”原”物理情景.

1 化“曲線”為“直線”

例1.把一根長為L的光滑鋼絲均勻地繞成一個高為h的彈簧,現把該彈簧豎直固定在地面上,讓一個小環穿在鋼絲上,并使其由靜止開始下滑,假設整個過程中彈簧的形變不計,求小環下滑過程中所用的時間.

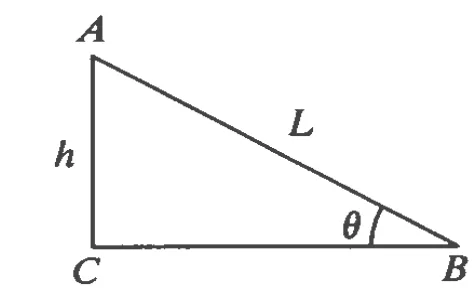
圖1

解析:小環下滑時,速度和加速度方向時刻在變化,是一個變速曲線運動,但是我們發現改變速度大小的力是重力沿鋼絲切線方向的分力,而大小是不變的,即加速度的大小是不變的.因此轉換物理情境:把小環沿曲線的下滑轉化為沿直線的下滑,即將彈簧以其中心軸為軸展開形成如圖1所示的三角形ABC,其中AC=h,AB=L.即把曲線問題轉變成了直線問題,小環沿彈簧下滑的運動等效為沿直線的下滑運動,把復雜問題簡單化了,由運動學公式得

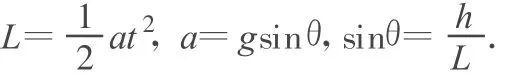
2 化“立體”為“平面”

例2.一位電腦動畫愛好者設計了一個“貓捉老鼠”的動畫游戲.如圖2所示,在一個邊長為a的大立方體箱子的頂角G上,老鼠從貓的爪子之間逃出,選擇了一條最短的路線,沿著箱子的棱邊奔向洞口,洞口處在大箱子的另一個頂角A處,若老鼠在奔跑中保持速度大小 v不變,并不重復跑過任一條棱邊及不再回到G點.聰明的貓也選擇了一條最短的路線奔向洞口(設貓和老鼠同時從 C點出發),則貓奔跑的速度為多大時,貓恰好在洞口再次捉住老鼠?

解析:這是一個立體的追擊問題,如果用求極值的方法是很繁瑣的,但如果轉換一下物理情境把大立方體展開鋪平如圖3所示,就會發現GA連線就是貓追老鼠的最短路線,這樣問題就變得非常簡單了.

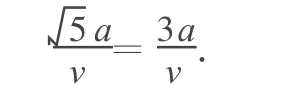
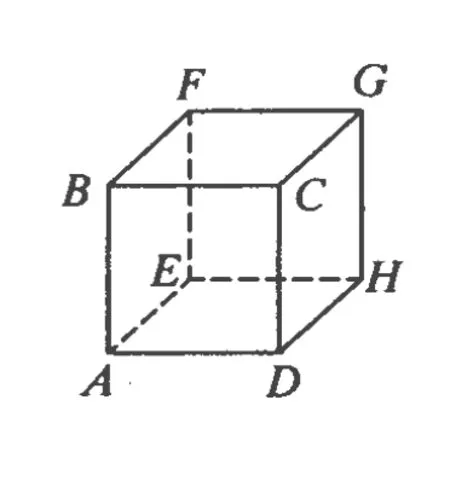
圖2

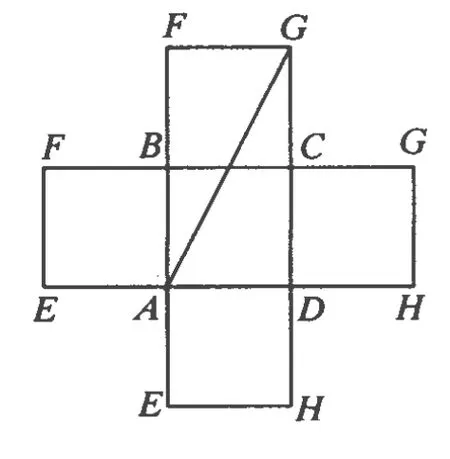
圖3

3 化“間斷”為“連續”

例3.回旋加速器的D形盒最大半徑為R,兩盒間距為d,加速電壓為 U,磁感應強度為 B.用它加速一個帶電粒子,則帶電粒子在回旋加速器中運動的總時間為多少?

解析:帶電粒子間斷地在電場中做勻加速直線運動,在磁場中做勻速圓周運動,運動的總時間等于電場力加速的總時間(tE)加上在磁場中運動的總時間(tB),一般來說,是先導出每次加速時間的表達式,再用數學知識求其和,繁瑣程度是可想而知.如果我們設計一個新的物理情境:把粒子間斷的加速轉化為連續不斷的加速直到飛離加速器.這樣問題就變成了初速度為零的勻加速運動了.由運動學公式和軌道半徑公式有

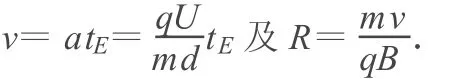
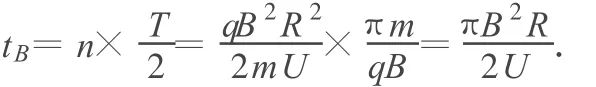
在加速器中運動的總時間為

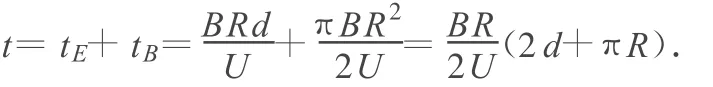
4 化“路線”為“光線”

例4.一輛汽車在軌道 MN上行駛的速度v1可達到50 km/h,軌道外的平地上行駛的速度 v2可達到40 km/h,與軌道的垂直距離為30 km的B處有一基地,如圖4所示.問汽車從基地B出發到離D點100 km的 A處的過程中最短需要多長時間(設汽車在不同路面上的運動都是勻速運動,啟動時的加速時間忽略不計)

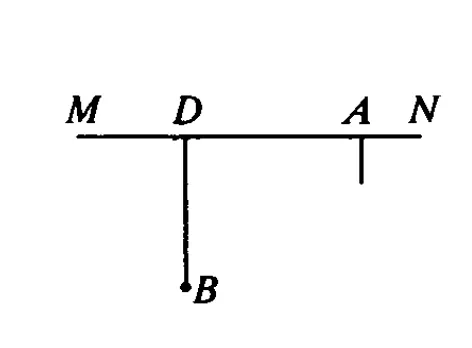
圖4

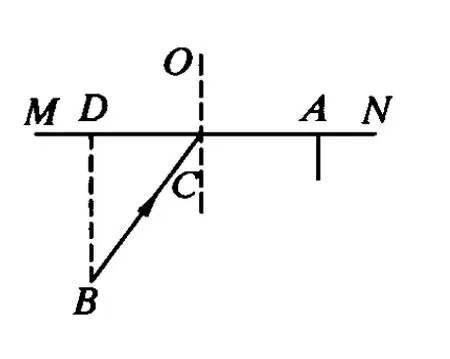
圖5

解析:常規方法是先寫出時間關于汽車上路點O到A點距離的函數式再求極值,但過程是比較繁瑣的.然而我們知道光在反(折)射現象中總是以時間最短的路徑傳播的.為此本題可以設計一個新情境:把汽車的運動路線類比為光線的傳播,這樣此問題恰好是全反射中的臨界狀態.由光學知識結合圖5得.

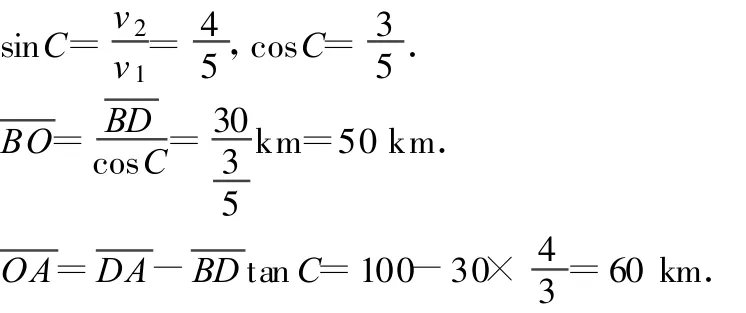
所以汽車運動的最短時間為

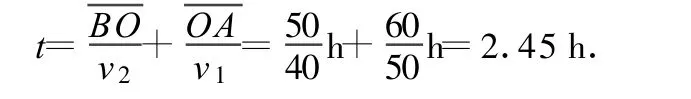
5 化“老鼠奔跑”為“力拉彈簧”

例5.(第4屆全國中學生物理競賽試題)老鼠離開洞穴沿直線前進,它的速度與到洞穴的距離成反比,當它行進到離洞穴距離為d1的甲處時的速度為v1,則它行進到洞穴為d2的乙處時,又用去的時間是多少?

解析:這道競賽題一般多采用圖像法、分割法等等,但都沒有離開題干敘述的實際情境,解答過程也不夠簡捷,如果轉換其情境聯想到汽車以恒定功率啟動的情形:速度與牽引力成反比,即v=.再使牽引力隨位移成正比(F=kx)變化,這樣汽車的啟動過程中速度就與位移成反比了,即v=.由于彈簧的彈力與受力端的位移成正比,于是便把“老鼠的奔跑”轉換為“外力以恒定的功率拉伸彈簧”的運動情境,問題就便于解決了.

對彈簧的端點由動能定理得

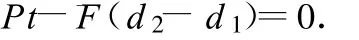
綜上,轉換物理情景對于解決物理問題十分重要,而轉換為不同性質的情景更有某種特殊的作用.