基于Matlab的Hertz接觸參數(shù)和主曲率差函數(shù)關(guān)系的擬合

劉勝超，王東峰，喻煒

(1.洛陽軸研科技股份有限公司 精密軸承制造部，河南 洛陽 471039；2.北京市三一重機有限公司，北京 102206)

符號說明

a—— 接觸橢圓的長半軸

b—— 接觸橢圓的短半軸

Dpw—— 球組節(jié)圓直徑，mm

Dw—— 球徑，mm

fi—— 內(nèi)溝曲率系數(shù)

fe—— 外溝曲率系數(shù)

F(ρ)——主曲率差函數(shù)

Fa—— 軸向載荷，N

k—— 接觸橢圓的橢圓率

K(e)——第一類橢圓積分

L(e)——第二類橢圓積分

Z—— 球數(shù)

ρ1Ⅰ——球在軸向平面的主曲率

ρ1Ⅱ——球在徑向平面的主曲率

ρ2Ⅰ——套圈在軸向平面的主曲率

ρ2Ⅱ——套圈在徑向平面的主曲率

α——初始接觸角，(°)

φ——橢圓積分變量

γ——無量綱參數(shù)，γ=(Dw/Dpw)cosα

Hertz接觸參數(shù)求解過程中，K(e)，L(e)和k是由循環(huán)迭代的方法求得的，迭代次數(shù)非常多，每次迭代都需要求解K(e)和L(e)，計算量大。這里利用Matlab曲線擬合工具箱，對K(e)，L(e)，k分別與F(ρ)進行擬合，得到它們和主曲率差函數(shù)F(ρ)的表達式，用擬合的結(jié)果求解給定型號軸承的其他Hertz接觸參數(shù)，并與Hertz接觸理論值以及最小二乘法線性回歸法(回歸法)得到的簡化式[1]求得的結(jié)果進行對比。

1 Hertz接觸參數(shù)

下面主要介紹與橢圓積分以及橢圓率計算相關(guān)的一些Hertz參數(shù)，其他參數(shù)不再贅述，可見文獻[2-3]。

1.1 接觸點的主曲率

在接觸點，球與溝道表面的主曲率描述了球和溝道表面在接觸點的幾何特征，其影響到接觸應力與變形及軸承動態(tài)性能[4]。球和溝道表面的主曲率計算方法見表1。

表1 球軸承接觸點主曲率計算公式

主曲率差及主曲率和分別為

(1)

∑ρ=ρ1Ⅰ+ρ1Ⅱ+ρ2Ⅰ+ρ2Ⅱ。

(2)

1.2 橢圓積分

第一類完全橢圓積分為

(3)

第二類完全橢圓積分為

(4)

橢圓率為

k=b/a。

(5)

F(ρ)可以由K(e)，L(e)和k表示為[5]

(6)

2 擬合法及回歸法

Matlab中提供的曲線擬合工具箱(Curve Fit Toolbox)可以對工作空間中的2組參數(shù)的數(shù)據(jù)點進行擬合，根據(jù)不同的擬合規(guī)則得到2個參數(shù)的表達式。這里利用Matlab曲線擬合工具箱，對K(e)，L(e)和k分別與主曲率差函數(shù)F(ρ)進行擬合，得到它們和主曲率差函數(shù)F(ρ)的表達式。

2.1 L(e)與F(ρ)的擬合

L(e)和F(ρ)的擬合曲線如圖1所示。L(e)和F(ρ)的數(shù)據(jù)能用四次多項式很好地擬合出來，即

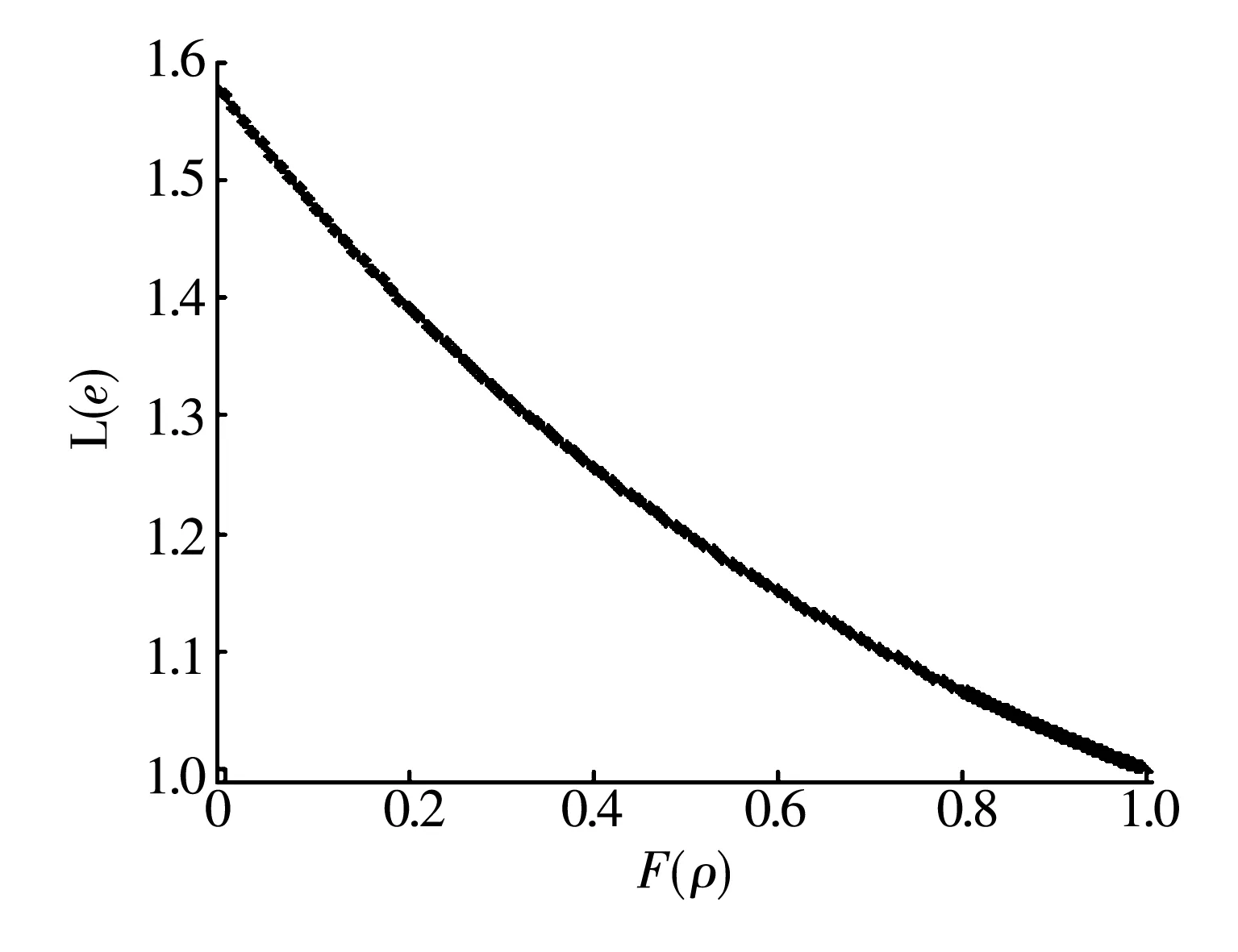
圖1 L(e)和F(ρ)的擬合曲線

L(e)=0.131 8F4(ρ)-0.449 4F3(ρ)+0.783 4F2(ρ)-1.036F(ρ)+1.57，

(7)

L(e)隨F(ρ)的增加而減小。

2.2 K(e)，k與F(ρ)的擬合

由于K(e)和k用多項式進行擬合時的誤差較大，采用三次樣條插值擬合法分別對它們與F(ρ)進行擬合，擬合的曲線如圖2、圖3所示。K(e)隨F(ρ)的增大而增大，且在F(ρ)趨近于1時趨于∞；k隨F(ρ)的增大而減小，二者幾乎呈線性關(guān)系。

圖2 K(e)和F(ρ)的擬合曲線

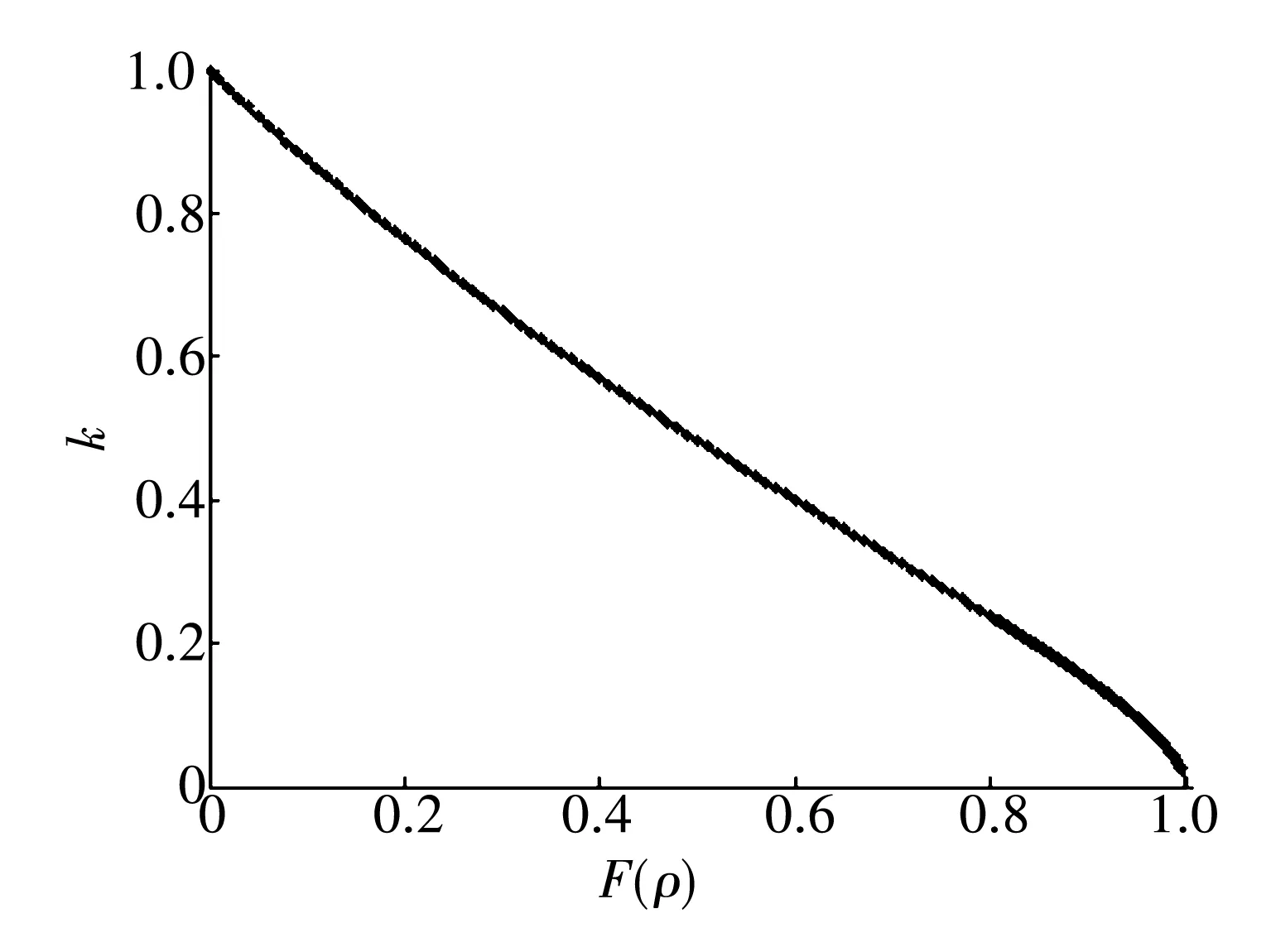
圖3 k和F(ρ)的擬合曲線

由于K(e)，k與F(ρ)擬合的結(jié)果無法用簡單的解析式表示出來， 因此將擬合結(jié)果保存至Matlab主工作區(qū)中KeFitted和kFitted兩個mat文件，求解時，在主程序中調(diào)用這2個函數(shù)來計算K(e)和k。

2.3 回歸法

由文獻[1]知，由回歸法求得的k，L(e)和K(e)的簡化關(guān)系式為

(8)

(9)

(10)

3 實例分析結(jié)果

表2 球軸承參數(shù)

表3和表4分別給出了由擬合法和回歸法得到的7208C/P4和B7019C/P4軸承的接觸參數(shù)值，并比較了其與Hertz接觸理論值的相對誤差。結(jié)果顯示，擬合法與Hertz接觸理論值之間的誤差更小，最大不超過0.6%；而回歸法的最大誤差將近1.8%。所以，擬合法不僅可行，而且更為準確。

表3 7208C/P4不同方法求得的接觸參數(shù)值及相對誤差

表4 B7019C/P4不同方法求得的接觸參數(shù)值及相對誤差

4 結(jié)束語

借助Matlab擬合出了橢圓積分、橢圓率與主曲率差函數(shù)的關(guān)系，用該擬合方法求解Hertz接觸參數(shù)避免了大量的循環(huán)迭代過程，節(jié)省了計算時間，同時由該方法計算得到的參數(shù)值比回歸法得到的參數(shù)值更為精確。