基于分塊不變矩特征的瓷磚分類識別的研究*

卞玉麗,鄭力新,晏來成,徐園園

(華僑大學 信息科學與工程學院，福建 廈門361021)

我國是瓷磚生產大國，生產企業眾多。在一些中小企業中,由于生產條件、成本等因素的制約，往往多種花紋的瓷磚共用一條生產線，主要靠大人工將不同類別的瓷磚分開，勞動強度大，效率低下且出錯率高。國內已展開與瓷磚相關的研究，如瓷磚的顏色分類、表面檢測等,當前大部分的研究內容，不管是分類還是缺陷識別，都涉及當前瓷磚與模板庫中的瓷磚進行比對匹配。參考文獻[1]檢測缺陷前根據瓷磚的邊緣進行配準，然后再匹配，配準前利用Hough變換檢測瓷磚的4個邊緣，計算量大，且檢測結果易受到噪聲干擾。參考文獻[2]在分類前假定生產線上瓷磚的擺放方式是固定的，這樣固然可以省去配準的步驟，但是也會使實用性大打折扣，因為生產線瓷磚的擺放方式不可能是固定的。參考文獻[3]利用遺傳算法進行配準，配準后再用模板匹配識別，由于配準和匹配都比較耗時，因此實時性較差，很難應用于生產現場。在這種背景下，找到一種快速、與擺放位置無關或者關系較小的特征對于瓷磚的分類識別具有重要意義。本文首先通過形態學邊緣檢測算子檢測瓷磚的花紋，然后將瓷磚分成4×4的子塊，計算每個子塊的Hu不變矩，選取其中第1個和第4個最穩定的兩個矩作為本子塊的特征，16個子塊的特征全部被提取后，輸入BP神經網絡(Back Propagation Network)進行分類識別。

1 特征提取

1.1 邊緣檢測

對于分類識別問題，特征的選取具有極其重要的作用。對于瓷磚這樣表面具有明顯花紋的對象，選擇花紋作為分類依據是非常自然的選擇，且已有一些論文采用紋理特征，具體來說是采用灰度共生矩陣作為分類的依據。

圖1中的瓷磚圖片里充滿著肉眼很難發現的細小的紋理，但是之所以稱其為一類，不是由這些極小的細節決定的，而是由其宏觀的由若干個方格組成的圖案決定的。如果采用灰度共生矩陣，那些過小的細節被不太必要地考慮進去，這樣不僅使得程序運行速度較慢，而且過多的冗余信息可能會影響分類的正確率。

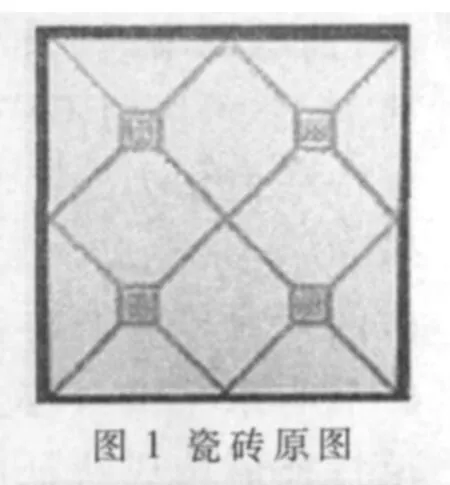
明顯的花紋形狀和走向是分類的主要依據，基于這一事實,本文首先通過邊緣檢測將花紋提取出來。圖2是對圖1 Canny邊緣檢測的結果。Canny等常見邊緣檢測算子歸根結底是對圖像進行求導得到的，而瓷磚的表面其實有些許細小的、無規律的紋理，這些肉眼都無法看清楚的紋理對分成不同類別的瓷磚沒有太多價值（當然，如果待分類的瓷磚只有極小的紋理不同時則令當別論），且若處理不當還會產生負面影響。

形態學梯度的定義為：

形態學梯度是通過膨脹后的圖像減去腐蝕后的圖像得到的。膨脹和腐蝕都可以指定結構元素的形狀和尺寸，較大尺寸的結構元素能夠檢測明顯花紋，較小尺寸的結構元素則檢測細小的花紋。本文采用圓形結構元素，尺寸為9×9。按照以下次序進行處理即可：RGB圖像→灰度圖像→圖像中值濾波去除噪聲→形態學邊緣檢測→二值化→腐蝕運算消除小的干擾點。圖3是形態學方法檢測的邊緣圖像，較好地反映了原圖的花紋走向，可以作為分類的依據。

1.2 矩特征[4]

不變矩是圖形的一種統計特征，它利用圖像的灰度分布的各階矩來描述圖像灰度的分布特征，在模式識別、目標分類中得到了廣泛的應用。

1.2.1 原點矩

二維原點矩的定義為：

對于離散圖像,通常近似為：

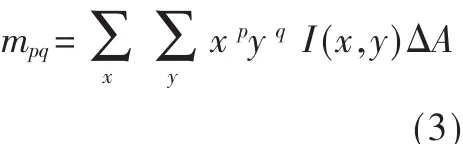
其中,ΔA表示像素的大小。

1.2.2 中心矩

然而，更多需求的是基本不變量，即希望得到的特征量與物體的位置、大小(即旋轉)無關。中心矩具有位置無關性，其定義為：

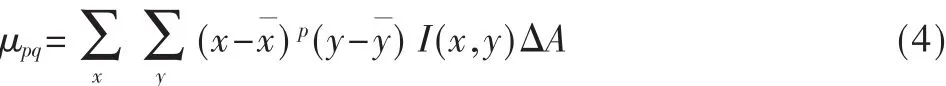
1.2.3 不變矩

中心矩具有平移不變性，即其僅對位置變換保持不變，而對旋轉則不具有不變性。為了得到旋轉和尺度不變性，需正規化中心矩，于是定義：

在此基礎上可以計算出7個不變矩：

1.3 分塊的矩特征提取

1.3.1 分塊特征選擇

表1 3種類別12種瓷磚的7個不變矩數據

表1是3種類別12種瓷磚的7個不變矩數據。可以看出，同一類別的瓷磚的不變矩中有多個表現較為不穩定，第5、6、7個，即便是同一塊瓷磚拍攝的多張照片之間也會有較大出入；但有些矩，比如第1、2、4個，則表現相對較為穩定。如果僅僅采用穩定的兩個或者3個矩特征作為分類的依據，數量太少，勢必會使分類精度下降，尤其當瓷磚之間的花紋差別不大時更為明顯。同時，不變矩描述的是圖像的整體特征，對局部信息的刻畫較差，即便不存在部分不變矩不穩定的情況也是如此。在這種背景下，本文首先將瓷磚分成4×4個小塊，然后計算每個小塊的不變矩，從中選取兩個較為穩定的，即整體共32個特征作為一個瓷磚的特征向量。這樣既去掉了不穩定的高階矩，同時，采取分塊的思想后，瓷磚的每個子部分都有相對應的矩，雖然對于子部分而言矩仍是全局特征，但對于整體來說，矩則變成了局部特征，描述刻畫對象的能力就更強了。

通過分析表1可以發現，前4個不變矩比較穩定，尤其是第1個、第2個及第4個距的數據在同類瓷磚之間比較接近，適合作為識別特征。本文選擇第1個與第4個不變矩（為了敘述方便,文中將7個不變矩分別簡稱一階矩、二階矩等）作為每個子塊的特征。

1.3.2 特征不變處理

不變矩本身與瓷磚的大小、擺放位置無關，具有較好的魯棒性，但是由于進行了分塊，這樣矩就與位置相關了。瓷磚在生產線上的擺放應該是隨機的，為了更具有一般性,本文假定瓷磚為關于圓心不對稱的圖形。

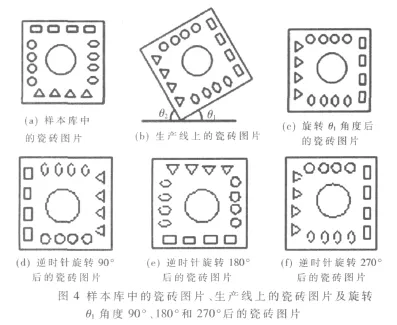
圖4(a)是訓練樣本庫中已知類別的某種瓷磚圖片，而圖4(b)是生產線上同類別的一個瓷磚圖片。可以看出,要想正確判斷出瓷磚的類別,必須將其旋轉成圖4(a)中的位置。但在分類之前根本無法判斷它是屬于哪種類別，更別說將其旋轉成所謂的正確位置了。本文的思路是，對于某一待識別的瓷磚，首先找出其最小外接矩形，由于瓷磚基本都是方形的，因此，最小外接矩形4個邊就是其4條邊線。分別計算最小外接矩形的4條邊與水平 線的 夾角,分 別為 θ1、θ2，找 出 它 們 中 較 小 的 那 個(如θ1)，然后根據較小的角出現的位置,對應地將瓷磚順時針或者逆時針旋轉 θ1角度，圖4(b)旋轉之后變成了圖4(c)。可以看出此時與圖4(a)還是不同，但將圖4(a)逆時針旋轉 270°后即為圖 4(f)，就與圖 4(c)一樣了。圖 4(d)、圖 4(e)、圖 4(f)分 別 是 將 圖 4(a)逆 時 針 旋 轉 90°、180°、270°后形成的3張圖片。那么同類別待識別的瓷磚，在將其按較小角θ1旋轉至水平位置后，總是可以與圖4(a)、圖 4(d)、圖 4(e)和圖 4(f)這4幅圖片中的一個相同。

綜上所述，解決分塊后位置相關性問題可以總結為：訓練網絡時，首先將每個樣本旋轉至水平位置，提取其16個子塊的不變距作為特征值 （共32個），再將32個特征值作為一個特征向量。分別將樣本圖片逆時針旋轉 90°、180°、270°后再分塊提取特征， 這樣一個訓練瓷磚圖片對應4個特征向量。分類識別時，將待識別的瓷磚沿與水平線最小夾角旋轉后，提取16個子塊的不變矩特征值構成特征向量，然后將特征向量作為識別網絡的輸入。這樣不管待識別的瓷磚位置如何，都能被正確地分類識別。

2 分類

2.1 網絡結構[6-7]

BP神經網絡是應用最多的一種神經網絡，它把網絡的學習過程分為正向傳播和反向傳播兩種交替過程，輸入的信號經輸入層、隱含層的神經元最終向前傳播到輸出層給出結果。如果在輸出層得不到期望的結果，則轉入逆向傳播過程，期望值與實際值之間的誤差反向傳播回去。通過修改各層神經元權值使得誤差減小，然后再轉入正向過程，如此反復，直至誤差滿足要求為止。本文采用的BP網絡具有三層，輸入層有32個點，輸出4個神經元。某個神經元輸出為1代表結果為本類瓷磚，如0010代表結果為第2類瓷。由于S函數的特點，輸出實際上很難是絕對的1或0，在本文中，輸出0.9代表1,0.1代表0。隱層神經元的個數具有一定的隨意性，可以根據實際情況作相應的調整，本文選8個隱層神經元。整體的網絡結構如圖5所示。

2.2 避免局部極小值[6]

BP算法在解空間中尋找能夠將誤差最小化的網絡權值，由于S函數為非線性函數，誤差曲面可能包含多個局部極小值，在搜索時有可能陷入到局部極小值中去，這是要盡量避免的。前文所述將初始值隨機取值也是避免局部極小值的一種手段，除此之外，本文還采用以下措施。

(1)增加動量因子。帶有附加動量因子的權值調整公式為：

其中，?為動量因子，一般取0.01~0.95。

增加動量因子后，在修正權值時,不僅要考慮誤差在梯度上的作用，而且還要考慮在誤差曲面上變化趨勢的影響。

(2)改變學習速率。較大的學習速率能夠在訓練初期加快收斂過程，然而當誤差較小時，過大的學習速率可能會越過誤差最小值點，這樣反而不利于最優值的求取。本文是在訓練過程中逐漸減小學習速率。

2.3 神經網絡識別

對每個子塊,本文首先嘗試選取三種特征類型：單個一階不變矩，一階、二階兩個不變矩以及一階、四階兩個不變矩。有4種類別的訓練樣本，如圖6所示，每種類別20個。測試圖片每種類別10個，以兩種不同擺放方式，共獲取20張圖片。程序基于VC++2008實現，主要分為訓練與識別兩部分[5]。訓練誤差曲線如圖7~圖9所示。

三種特征類型期望的最后誤差都是0.001。可以看出，單獨采用一階矩作為特征在8001代時誤差仍為0.001 344；采用一、二階矩表現稍微好些，8001代時誤差是0.001 167；而采用一、四階矩時誤差明顯減小，在5 023代時，誤差已經在0.001之下了。與訓練相一致，測試時，4種瓷磚共80張測試樣本，采用一階不變矩特征出現兩張誤判，一、二階不變矩組合兩張誤判，而一、四階不變矩組合0張誤判。由此可見，利用一、四階距組合識別準確率很高。另外，每個瓷磚從特征提取到給出正確結果的時間為1 s，具有一定的實時性，能滿足生產線上的需求。

本文系統地介紹了基于分塊不變距特征的瓷磚分類識別的方法。利用形態學邊緣檢測提取瓷磚的花紋；再利用Hu不變矩針對部分不變矩不穩定的問題提出分塊思想，分塊后提取每個子塊最穩定的不變矩作為本子塊的特征，從而解決了分塊后帶來的位置相關性問題；最后用BP神經網絡進行訓練來分類識別。實驗結果，表明此方法效果較好、速度快、準確率高，且對瓷磚的擺放位置不作要求，可以實現瓷磚在線生產上的分類識別的實時性的需求。該方法具有一定的通用性，對以矩作為特征的分類識別問題具有一定的參考意義。

[1]劉笛.墻地磚顏色的自動分類研究[D].廣州:華南理工大學，2004.

[2]蘇彩虹.墻地磚質量自動檢測技術的研究[D].廣州:華南理工大學，2004.

[3]鄭力新,姚強，周凱汀.利用遺傳算法實現模板匹配的瓷磚分選[J].華僑大學學報（自然科學版）,2010,31(6):632-635.

[4]李國祥,張顯全，秦芳遠.基于不變矩和BP神經網絡的剪紙紋樣識別[J].計算機工程與應用,2010,46(29):158-60.

[5]張錚,王艷平，薛桂香.數字圖像處理與機器視覺—Visual C++與 Matlab實現[M].北京:人民郵電出版社，2010.

[6]蔣憲剛.數字圖像模式識別工程軟件設計[M].北京:水利水電出版社，2008.

[7]韓力群.人工神經網絡理論、設計及應用[M].北京:化學工業出版社，2007.