客運專線高架車站的減振設計研究

馬 莉，王 瀾，高芒芒，熊建珍，宣 言，方 興

(中國鐵道科學研究院 鐵道科學技術研究發展中心，北京 100081)

隨著我國高速鐵路的迅猛發展，客運專線的高架車站已經成為集鐵路、地鐵、公交等多種交通方式為一體的大型綜合交通樞紐。高速列車通過高架車站時引起的振動會直接影響旅客候車或換乘的舒適性，由此對車站的減振降噪技術提出了較高的要求。本文以某客運專線鐵路高架車站為實例，建立列車—無砟軌道—站房結構模型，結合現場試驗結果對模型的準確性進行了驗證，并對不同減振方案的效果進行分析。

1 工程概況

某客運專線鐵路高架車站由主站房和站臺雨棚組成，站臺雨棚為一層單鋼結構，位于主站房的兩側，與主站房設防振縫分開。

主站房結構采用建橋一體化結構形式，自下而上依次為出站層、站臺層和候車廳。出站層地面高程為－9.250 m，層高10.500 m;站臺層樓面高程為1.250 m，層高9.250 m;候車廳樓面高程為10.500 m;屋面為曲面鋼網架(局部為49 m的張弦梁)，最高點高程為38.200 m，最低點高程為21.970 m。站臺層立柱為矩形鋼管混凝土柱，候車廳立柱為圓形鋼管混凝土柱和樹形組合鋼管混凝土柱，內灌C40混凝土。

站臺層的站線規模為8站臺16線(含2條高速正線)，有1個基本站臺和7個中間站臺。站線區主要由10座3跨橋式布置為(30.1+49.0+30.1)m的箱型預應力混凝土連續梁及其相互之間的站臺梁組成。墩臺均采用實體橋墩，橋墩采用矩形截面，墩臺和墩身采用C30混凝土。位于到發線連續梁中墩上的立柱，穿越連續梁橫梁中預設的孔道，支立于橋墩頂面，位于橋臺上的立柱直接支立于墩臺頂。由于正線橋梁與兩側的到發線橋梁共用橋墩，當高速列車通過正線時，正線橋梁的振動將通過橋墩和橋墩上的立柱向上傳遞至候車廳。

2 高架車站減振分析

2.1 模型建立

采用有限元軟件MIDAS建立站房主體結構模型，模型長113.0 m，寬163.5 m，包含出站層、站臺層、設備夾層、候車廳以及鋼網架屋蓋，以梁式受彎桿件和三角形或矩形板單元為基本單元，如圖1所示。通過對站房主體結構和正線連續梁自振特性的分析，站房主體結構前20階振型均為鋼網架屋蓋和候車廳樓面的局部振動，圖2和圖3分別為鋼網架屋蓋和候車廳樓面的典型振型圖;正線連續梁的自振特性計算結果見表1，第1階對稱豎彎和第2階反對稱豎彎的振型圖如圖4和圖5所示。

圖1 車站主站房結構有限元模型

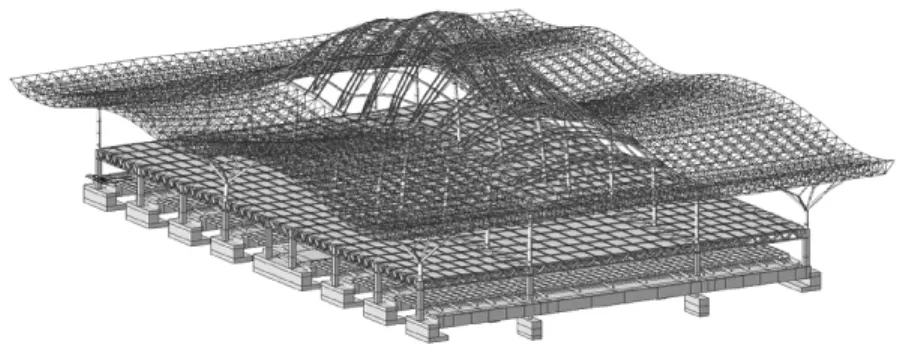
圖2 車站主體結構第6階振型

圖3 車站主體結構第12階振型

圖4 正線連續梁第1階振型

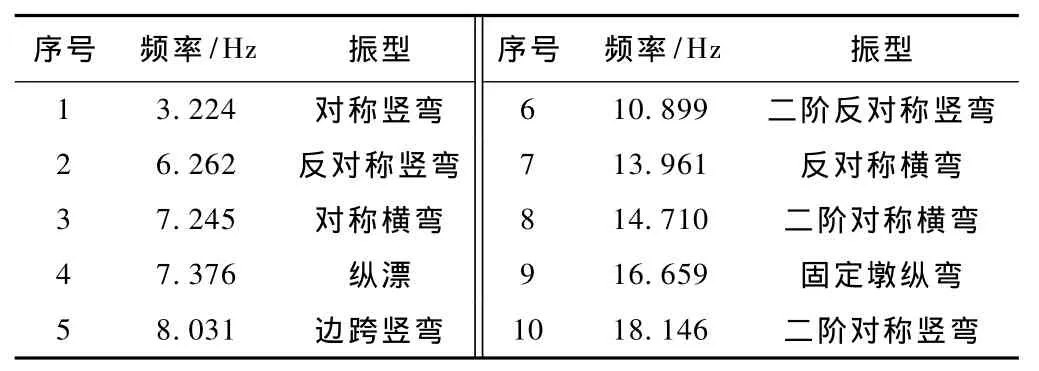
表1 正線連續梁自振頻率表

圖5 正線連續梁第2階振型

2.2 模型驗證

車站主站房模型作為子結構進入列車—無砟軌道—站房結構耦合振動分析程序，可計算出列車正線通過車站時站內各點的動力學響應。基于該車站現場振動試驗采用的試驗列車為CRH2高速動車組(車輛編組6動2拖)，且300 km/h車速的試驗樣本數目較多，對模型進行驗證時，列車采用CRH2高速動車組，輪軌激勵采用實測軌道不平順，計算車速為300 km/h。

1)自振頻率的對比

現場振動試驗采用環境微振動法對正線橋梁自振特性進行測試。實測以中跨49 m梁振動為主的豎向自振頻率為3.580 Hz，對應于理論計算的第1階對稱豎彎，計算值為3.224 Hz;以邊跨32 m梁振動為主的豎向自振頻率為6.910 Hz，對應于理論計算的第2階反對稱豎彎，計算值為6.262 Hz。實測值略高于計算值，兩者基本吻合。

2)振動響應對比

根據車站候車廳的平面布置，車站橫向距離正線中心線 0，17，28 m處的區域為旅客候車休息區，人員較為密集，樓面的振動將直接影響旅客候車的舒適性，計算時主要考慮上述敏感區域的樓面振動。候車廳樓面豎向加速度的計算值與實測值的對比如表2所示。通過比較可知，實測值和計算值均呈現正線中心線上方樓面振動劇烈，加速度值較大，較遠處振動逐漸衰減，數值減小的特點。實測值略高于計算值，兩者之間誤差較小，理論分析結果與實測值吻合良好，能夠反映結構的實際振動情況。

表2 高架候車廳樓面豎向振動加速度實測值與計算值比較m/s2

2.3 減振優化方案

鑒于本文工程案例中高架車站已經建成，相對于車站建筑結構內部的減振，對正線軌道結構進行減振更具效果，不僅可以直接減小正線橋梁傳遞至候車廳的振動，而且軌道減振措施比較容易實施，也利于日常養護和維修。針對列車正線通過該車站的設計速度為350 km/h，且以CRH2型動車組居多的情況，提出三種軌道減振優化方案，即提高扣件彈性、軌道板下鋪設橡膠彈性墊層以及使用鋼彈簧浮置板軌道代替原來的雙塊式無砟軌道。采用上述三種軌道減振優化方案對車站進行仿真分析時，列車參數選取CRH2型動車組參數(車輛編組為6動2拖)，車速為350 km/h，輪軌激勵采用實測軌道不平順。

1)提高扣件彈性

在有砟軌道中，軌道彈性主要由道床提供，而在無砟軌道中，軌道彈性主要由扣件提供，因此扣件彈性對減振具有重要作用，可以減小對下部軌道結構或橋梁的沖擊作用。在高速鐵路無砟軌道結構中，應用最為廣泛的扣件是日本的直結4K型和8K型、德國的Vossloh300型、Krupp ECF型以及 Pandrol推出的Fastclip扣件。日本直結型扣件彈性主要由軌下墊板提供，靜剛度一般為30 kN/mm，動靜剛度比≥1.5;德國扣件彈性主要由鐵墊板下的彈性基板提供，靜剛度一般為25 kN/mm，動靜剛度比≤1.5;Pandrol推出的Fastclip扣件彈性主要由軌下墊板提供，墊板剛度為40～55 kN/mm。針對不同的扣件彈性，在模型計算過程中通過改變鋼軌支承剛度對比分析車站的動力響應。在本文所取計算參數條件下，當鋼軌支承剛度為25～80 kN/mm時，候車廳樓面豎向振動加速度隨鋼軌支承剛度的增大而增大，大體上呈線性分布，如圖6所示，提高扣件彈性可以有效減振，鋼軌支承剛度每減小1 kN/mm可使候車廳樓面振動加速度減小0.005 m/s2。

針對高速鐵路高架候車環境，目前國內外尚無規范、標準對人體舒適度可接受的樓蓋振動限值做出規定。美國ATC(Applied Technology Council)于1999年發布《減小樓板振動》設計指南中建議:醫院手術室、住宅及辦公室、商場、室外人行天橋等不同環境下的樓蓋豎向振動峰值加速度限值分別為0.025 m/s2、0.05 m/s2、0.15 m/s2和0.5 m/s2。鐵路客運車站的候車環境與室外人行天橋有類似之處，候車廳樓面豎向振動峰值加速度不宜超過0.5 m/s2。根據圖6，考慮到動靜剛度比，該車站鋼軌支承靜剛度適宜在25～50 kN/mm之間。

圖6 候車廳樓面豎向振動加速度與扣件彈性關系圖

2)軌道板下鋪設橡膠彈性墊層

在本文的高架車站中，正線軌道采用雙塊式無砟軌道，如果在軌道板下設置20 mm厚橡膠彈性墊層，可以降低軌道支承剛度，減小正線橋梁的振動。在計算模型中使用間距相等的分布式支承彈簧來模擬橡膠墊層的彈性，支承彈簧間距定為0.6 m，剛度取為40 kN/mm。在本文所取計算參數條件下，候車廳樓面的加速度對比如圖7所示。無砟軌道下鋪設橡膠彈性墊層相對于未采用減振措施時，可使候車廳樓面的振動減小約10%。

圖7 候車廳樓面加速度對比(方案二)

3)采用鋼彈簧浮置板道床結構

鋼彈簧浮置板道床結構具有良好的減振性能，在城市地鐵中得到廣泛應用，但尚未在高速鐵路中得到應用。按照支承方式劃分，鋼彈簧浮置板主要有側置彈簧式和內置彈簧式兩種，如圖8所示。地鐵車速為80 km/h，而高鐵車速在250 km/h以上，如果在高速鐵路軌道結構中使用鋼彈簧浮置板道床，考慮到安裝和檢修的方便，宜采用側置彈簧式，而且需要對其進行橫向限位，使之能夠牢固地固定在基礎和橋梁上。

圖8 鋼彈簧浮置板

針對本文的高架車站，按照《城市軌道交通彈簧浮置板軌道技術標準》中的相關規定，對鋼彈簧浮置板的尺寸和參數進行設計。高架車站正線橋梁鋪設4塊鋼彈簧浮置板，每塊浮置板長度為27.2 m，寬度為2.8 m，厚度為0.77 m，鋼彈簧隔振器間距為4.53 m，隔振器的垂向剛度為39.76 kN/mm，橫向剛度為44.37 kN/mm。為了保證高速列車通過時浮置板的穩定性，需要在浮置板的橫向設置擋塊。

在本文所取計算參數條件下，候車廳樓面的加速度對比如圖9所示，軌道結構采用鋼彈簧浮置板道床相對于原來的無砟軌道可使候車廳樓面的振動減小約25%。

圖9 候車廳樓面加速度對比(方案三)

3 結論

本文通過建立某客運專線鐵路高架車站模型，采用三種不同軌道減振方案，對其進行列車—無砟軌道—站房結構耦合振動分析，并對不同方案條件下的減振效果進行了分析，得出如下結論:

1)提高扣件彈性，減小鋼軌支承剛度可以減小該車站的振動響應，鋼軌支承剛度每減小1 kN/mm可使候車廳樓面振動加速度減小0.005 m/s2，為了保證旅客候車的舒適度，鋼軌支承靜剛度適宜在25～50 kN/mm之間。

2)在軌道板下設置20 mm厚橡膠彈性墊層可使該車站候車廳樓面的振動減小約10%。

3)將鋼彈簧浮置板道床結構應用于客運專線高架車站可以起到很好的減振效果，可使該車站候車廳樓面的振動減小約25%，同時為了保證高速列車通過時浮置板的穩定性，需要在浮置板的橫向設置擋塊對其橫向進行限位。

［1］潘家英，高芒芒．鐵路車—線—橋系統動力分析［M］．北京:中國鐵道出版社，2008．

［2］辜小安，馬筠，楊宜謙，等．武廣客運專線長沙南站高架候車廳振動噪聲試驗研究階段報告［R］．北京:中國鐵道科學研究院，2009．

［3］趙國堂．高速鐵路無碴軌道結構［M］．北京:中國鐵道出版社，2006．

［4］孫立．減振型板式無砟軌道道床板受力分析研究［J］．鐵道建筑，2009(8):108-111．

［5］李君，蔡成標，徐鵬，等．減振型板式軌道合理剛度動力分析［J］．鐵道建筑，2010(5):105-107．