多頻激勵下氣動隔振系統(tǒng)非線性特性分析

鐘艷春，楊慶俊，包鋼

(哈爾濱工業(yè)大學 機電工程學院，黑龍江 哈爾濱，150001)

氣動隔振系統(tǒng)承載力大，有效行程大，隔振效果優(yōu)異，廣泛應用于儀器平臺、光學平臺、精密加工與檢測、艦船動力設備隔振、車輛懸掛等的振動隔離[1-5]。由于非線性微分動力系統(tǒng)的復雜性，空氣彈簧的彈性恢復力非線性對隔振系統(tǒng)特性的影響沒有同時得到有效研究。為了簡化計算過程，在大量的實際操作中，空氣彈簧或被近似處理成定剛度彈簧，或忽略空氣彈簧變形過程中有效面積以及其他參數改變后，由空氣彈簧內氣體的狀態(tài)確定彈簧的狀態(tài)[6]。近年來，有學者開始氣動隔振系統(tǒng)的非線性研究，Heertjes等[7]研究了氣體壓縮的非線性對傳遞率和導納的影響。尹萬建等[8]研究了空氣彈簧在單頻正弦激勵情況下的主共振，并認為激勵幅值與非線性剛度是影響空氣彈簧懸架非線性特性的主要因素，但是，沒有研究系統(tǒng)多頻激勵下的非線性特性。在非線性方程方面，周一峰等[9]建立了主動隔振體的非線性動力學方程，對求解強非線性自治系統(tǒng)的能量迭代方法加以改進，將其用于求解強非線性非自治系統(tǒng)，得到了主動隔振系統(tǒng)周期運動響應的解析表達式和振幅-頻率關系曲線。Nayfeh等[10]研究了平方和立方非線性系統(tǒng)在2個簡諧激勵共同作用下的組合共振和聯合共振情況。在此，本文作者首先從基本的實驗數據出發(fā)，得到空氣彈簧相對載荷隨高度的曲線，然后用三次多項式擬合該試驗曲線，得到彈簧恢復力與高度之間的關系式。將恢復力代入載荷運動動力學方程得到系統(tǒng)在3個簡諧激勵共同作用下的非線性平衡方程，利用多尺度法[11-13]對該非線性振動方程進行求解，分析各參數變化對系統(tǒng)幅頻特性的影響，以便為指導氣動隔振系統(tǒng)的設計提供理論依據。

1 空氣彈簧非線性模型

本文選用簡單的單腔氣彈簧對其進行非線性特性分析。氣動隔振系統(tǒng)簡化模型如圖1所示。圖1中：M為彈簧上的質量；K為空氣彈簧總剛度，c為考慮空氣彈簧自身阻尼在內的總阻尼；xb為基座振動，x為負載振動。

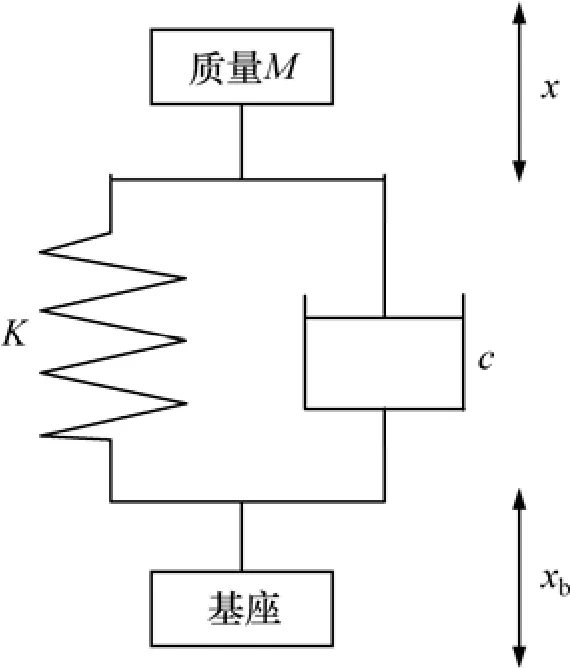
圖1 氣動隔振系統(tǒng)模型簡圖Fig.1 Schematic diagram of pneumatic vibration isolation system

1.1 空氣彈簧載荷

選用 Firestone 1M1A-1型空氣彈簧作為研究對象。空氣彈簧在初始充氣壓力為0.7 MPa時，不同高度下的絕對載荷如圖2所示。

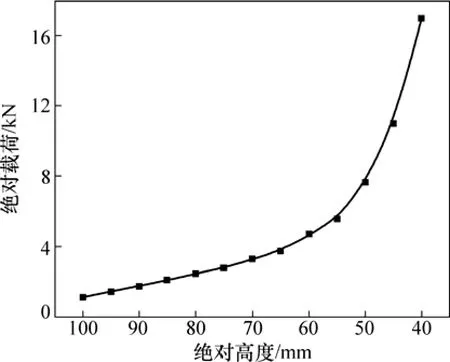
圖2 Firestone 1M1A-1型空氣彈簧絕對載荷隨高度變化曲線Fig.2 Absolute load curve with height of Firestone 1M1A-1 air spring

從圖2可以看出：與一般彈簧的特性不同，空氣彈簧的絕對彈力總是正值。但相對平衡位置，彈力可以有正有負：在平衡位置以上為負，在平衡位置以下為正。相對于平衡位置75 mm高度時的相對載荷如圖3所示。

1.2 空氣彈簧恢復力擬合

文獻[6]指出僅用三次多項式就能非常精確地擬合試驗曲線，采用太高的冪次一方面不會顯著提高精度，另一方面會使擬合剛度曲線光滑性變差。因此，本文采用三次多項式對該曲線擬合。空氣彈簧相對平衡位置的彈性恢復力F可以表示為：

式中：F為空氣彈簧相對平衡位置的彈性恢復力；x為載荷振動；xb為基座振動；k1為空氣彈簧的線性剛度；k2為二次非線性系數，k3為三次非線性系數。

以實驗所得的空氣彈簧相對彈力為原始數據，根據式(1)對其進行三次多項式擬合，擬合曲線如圖3所示。通過曲線擬合得到的三次多項式系數分別為k1=20.5 N/m，k2=3 063 N/m2，k3=212 797 N/m3。從圖3可以看出：擬合曲線和實驗數據重合性好。

圖3 Firestone 1M1A-1型空氣彈簧相對載荷多項式擬合曲線Fig.3 Relative load polynomial fitting curve of Firestone 1M1A-1 air spring

2 多頻激勵下氣動隔振系統(tǒng)非線性模型

考慮對于多頻激勵進行分析時，3個頻率激勵具有很好典型性，能很好地反映系統(tǒng)多頻激勵下的規(guī)律性，并且分析也簡單明了，因此，本文選用3個激勵頻率進行分析。假設基座激勵為：

式中：F1，F2和F3依次為3個外部激勵的幅值；Ω1，Ω2和 Ω3依次為 3個外部激勵的頻率；θ1，θ2和 θ3依次為3個外部激勵的初相角。

在其激勵下，系統(tǒng)的動力學方程為：

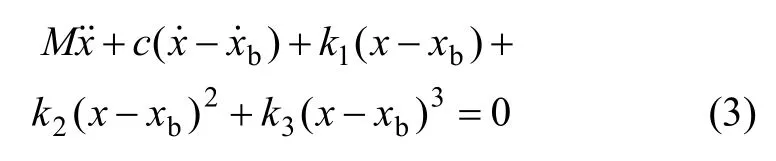
式中：M為載荷質量；c為系統(tǒng)阻尼系數。

設y=x-xb，則方程(3)可以寫為：

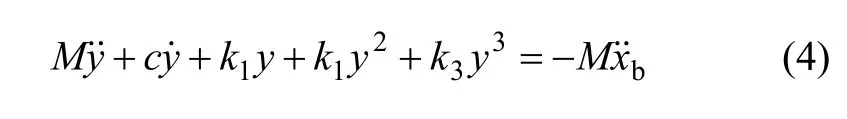
構造長度尺度 L=F1和時間尺度得到無量綱變量對式(4)進行無量綱化，則得到：式中

運用多尺度法對式(5)進行分析，設式(5)的近似解為：

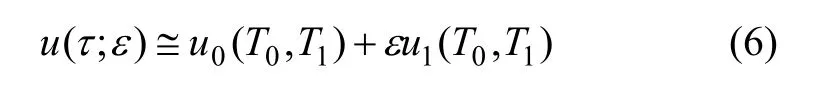
式中：T0=τ，T2=ετ分別為不同的時間尺度變量。

因此，關于τ的導數變成關于T0和T1的偏導數的展開式，即有

式中： Dn=? / ( ? Tn)。

將式(6)～(8)代入式(5)，并展開比較ε同次冪的系數，得到：

方程(9)的通解可以寫為：

將方程(11)代入方程(10)得到：

從式(12)可以看出：在 3個頻率激勵下，系統(tǒng)會出現超諧共振 2ωn≈1，3ωn≈1，亞諧共振 ωn≈2，ωn≈3，組合共振 ωm± ωn≈1，ωm± ωn≈2，ωm± ωn≈3，2ωm±ωn≈1，2ωm±ωn≈2，2(ωm±ωn)≈1，ωm± ωn± ωx≈1等。

下面討論 ω1±ω2+ ω3≈1的情況。引進調諧參數σ，令

將其代入(ω1+ω2+ω3)T0可以寫為：

由式(12)式可得，若

令式(14)和(15)α ˙ =γ˙= 0 得其穩(wěn)定解。得到下列方程組：

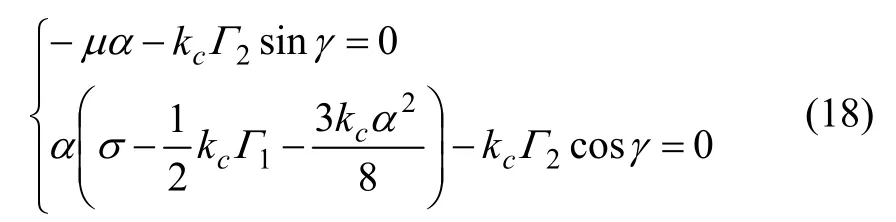
由式(18)可得頻率響應為：

聯合前面各表達式，并將其代入方程(19)得到頻率響應和各初始參數之間的關系為：

3 系統(tǒng)參數對頻率響應曲線的影響

方程(20)即為系統(tǒng)的頻率響應關系式，下面分別固定其他參數而變化其中1個參數，得到各主要參數對系統(tǒng)幅頻曲線的影響。圖4～7所示分別為各主要參數變化對系統(tǒng)幅頻特性影響的曲線。

圖4 激勵幅值變化時的組合共振幅頻曲線Fig.4 Frequency-response curves in differentexcitation amplitudes

圖 4 中，k1=20.5 N/m，k2= -3 063 N/m2，k3=21 279 N/m3，ω1=0.18，ω2=0.34，ω3=0.49，M=280 kg，c=140 N·s/m。從圖4可以看出：激勵幅值對非線性響應曲線有明顯影響；隨著激勵幅值的增大，組合共振的響應振幅也增大。并且隨著激勵幅值的增大，幅頻曲線的骨架曲線的彎曲程度變得更大，說明激勵幅值越大，系統(tǒng)非線性特性越明顯。

圖5中，其余各參數取值如下：k1=20.5 N/m，k2=-3 063 N/m2，F1=F2=F3=0.015 m，ω1=0.18，ω2=0.34，ω3=0.49，M=280 kg，c=140 N·s/m。從圖5可以看出：三次非線性系數直接影響幅頻響應曲線的非線性特性。當k3＞0時，幅頻曲線的骨架曲線向右彎曲，當k3＜0時，幅頻曲線的骨架曲線向左彎曲；k3的絕對值越大，曲線的彎曲程度越大；組合共振響應曲線的幅值也隨k3的絕對值的增大而增大。

圖5 三次非線性系數變化時的組合共振幅頻曲線Fig.5 Frequency-response curves in different cube nonlinear parameters

圖6 中，其余各參數取值如下：k1=20.5 N/m，k2=-3 063 N/m2，k3=21 279 N/m3，F1=F2=F3=0.015 m，從圖6可知，當載荷變小時，這種組合共振的幅頻曲線彎曲程度變大，非線性現象變得更明顯。

圖7中，其余各參數取值如下：k1=20.5 N/m，k2=-3 063 N/m2，k3=21 279 N/m3，F1=F2=F3=0.015 m，ω1=0.18，ω2=0.34，ω3=0.49，M=280 kg。從圖7可以看出：隨著阻尼系數的增大，組合共振響應曲線的幅值變小。而幅頻曲線的骨架曲線不受阻尼的影響，系統(tǒng)的共振域也基本不變。

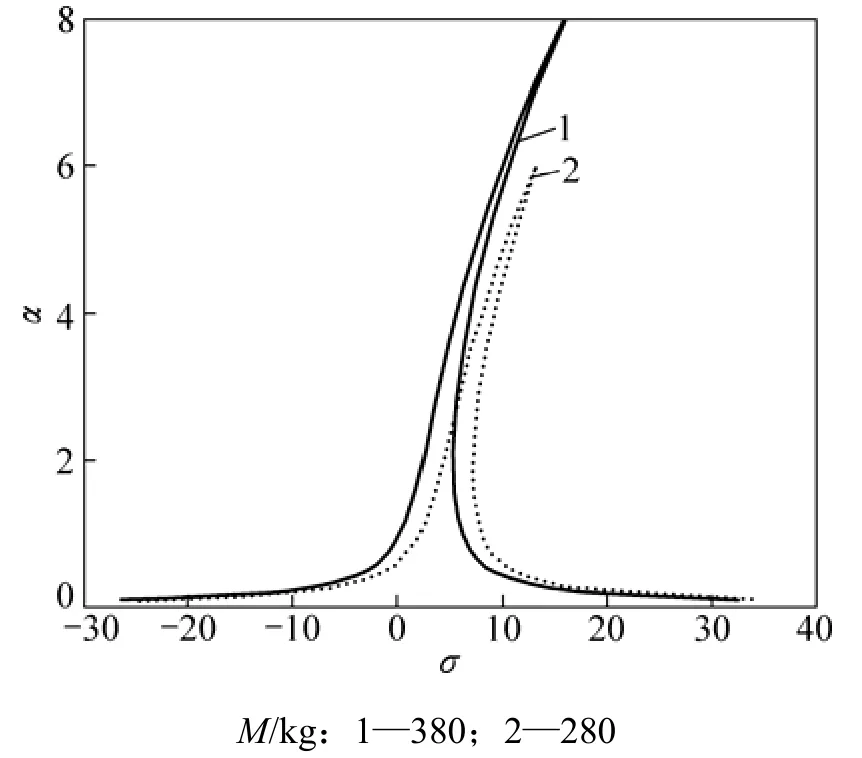
圖6 載荷變化時的組合共振幅頻曲線Fig.6 Frequency-response curves in different load masses

圖7 阻尼系數變化時的組合共振幅頻曲線Fig.7 Frequency-response curves in different damping coefficients

4 結論

(1) 根據實驗得到的空氣彈簧動載荷曲線，運用三次非線性多項式對其進行擬合，得到一定初始壓力下空氣彈簧相對平衡位置的非線性恢復力與高度的關系式，為對系統(tǒng)非線性求解奠定了基礎。

(2) 在3個頻率激勵下系統(tǒng)會出現超諧共振、亞諧共振、組合共振等情況。對 ω1+ω2+ω3≈1的組合共振進行分析，得到了頻率響應方程。

(3) 激勵幅值越大，系統(tǒng)非線性現象越明顯；三次非線性系數對系統(tǒng)非線性影響大，當k3＞0時，幅頻曲線的骨架曲線向右彎曲；，當k3＜0時，幅頻曲線的骨架曲線向左彎曲；載荷變小時，組合共振幅頻曲線彎曲程度變大；阻尼變小時，組合共振響應曲線的幅值變大，系統(tǒng)的共振域不受阻尼變化的影響。

[1] Kato T, Kawashima K, Sawamoto K, et al. Active control of a pneumatic isolation table using model following control and a pressure differentiator[J]. Precision Engineering, 2007, 31(3):269-275.

[2] CHEN Ping-chang, Shih Ming-chang. Modeling and robust active control of a pneumatic vibration isolator[J]. Journal of Vibration and Control, 2007, 13(11): 1553-1571.

[3] 徐偉, 何琳, 呂志強, 等. 船舶主機氣囊隔振系統(tǒng)動態(tài)特性分析[J]. 振動與沖擊, 2007, 26(7): 122-124.XU Wei, HE Lin, Lü Zhi-qiang, et al. Dynamic analysis of an air spring mounting system for marine main engine[J]. Journal of Vibration and Shock, 2007, 26(7): 122-124.

[4] Lee J H, Kim K J. A method of transmissibility design for dual-chamber pneumatic vibration isolator[J]. Journal of Sound and Vibration, 2009, 323(1): 67-92.

[5] Shimozawa K, TohtakE T. An air spring model with non-linear damping for vertical motion[J]. Quarterly Report of RTRI, 2008,49(4): 209-214.

[6] 陳燎, 周孔亢, 李仲興. 空氣彈簧動態(tài)特性擬合及空氣懸架變剛度計算分析[J]. 機械工程學報, 2010, 46(4): 93-98.CHEN Liao, ZHOU Kong-kang, LI Zhong-xing. Dynamic characteristics fitting of air springs and numerical analysis of air suspensions with variant stiffness[J]. Chinese Journal of Mechanical Engineering, 2010, 46(4): 93-98.

[7] Heertjes M, van de Wouw B. Nonlinear dynamics and control of a pneumatic vibration isolator[J]. Journal of Vibration and Acoustics.2006, 128(4): 439-448.

[8] 尹萬建, 韓鷹, 楊紹普. 空氣彈簧懸架系統(tǒng)在強迫振動下的動力學分析[J]. 中國公路學報, 2006, 19(3): 117-121.YIN Wan-jian, HAN Ying, YANG Shao-pu. Dynamics analysis of air spring suspension system under forced vibration[J]. China Journal of Highway and Transport, 2006, 19(3): 117-121.

[9] 周一峰, 唐進元, 何旭輝. 強非線性主動隔振系統(tǒng)的運動響應及傳遞率[J]. 中南大學學報: 自然科學版, 2005, 36(3):496-500.ZHOU Yi-feng, TANG Jing-yuan, HE Xu-hui. Response and transmissibility of strong nonlinear active isolation system[J].Journal of Central South University: Science and Technology,2005, 36(3): 496-500.

[10] Nayfeh A H. Combination tones in the response of single degree of freedom systems with quadratic and cubic non-linearities[J].Journal of Sound and Vibration, 1984, 92(3): 379-386.

[11] Nayfeh A H, Mook D T. Nonlinear oscillations[M]. New York:Wiley, 1979: 161-224.

[12] 劉延柱, 陳立群. 非線性振動[M]. 北京: 高等教育出版社,2001: 83-95.LIU Yan-zhu, CHEN Li-qun. Nonlinear vibration[M]. Beijing:High Education Press, 2001: 83-95.

[13] 楊紹普, 申永軍. 滯后非線性系統(tǒng)的分岔與奇異性[M]. 北京:科學出版社, 2003: 35-40.YANG Shao-pu, SHEN Yong-jun. Bifurcation and singularity of non-linear systems with hysteresis[M]. Beijing: Science Press,2003: 35-40.