基于RLS算法的記憶多項式預失真技術分析

陳寶文,韓 軍,張 航

(中國電子科技集團公司第五十四研究所,河北石家莊050081)

0 引言

功率放大器是現代通信系統中必不可少的組成部分。隨著通信技術的飛速發展,高頻譜利用率的高階調制技術(M-QAM)及多載波調制技術(OFDM)等得到了廣泛使用。然而這些無一例外的都屬于非恒包絡調制技術,對功率放大器的非線性非常敏感。而功放的非線性不僅會引起帶外頻譜擴張,產生鄰信道干擾,還會引起帶內失真,增加誤碼率,因此功放的線性化變得尤為重要。

功率放大器的線性化技術有很多種[1],常見的有功率回退法、前饋法、負反饋法和數字預失真法等。自適應數字基帶預失真法由于引入了自適應算法,并且在基帶進行處理,不涉及復雜的射頻信號處理并可以實時跟蹤功放的變化特性,因此可以很好地校正功放的非線性。

1 基本原理

數字基帶預失真技術的基本原理就是基帶信號首先經過預失真器的預處理,而預失真器的傳輸特性則剛好是功放傳輸特性的反函數,這樣最后經過放大器后輸出信號就只有線性的增益了,其基本原理如圖1所示。

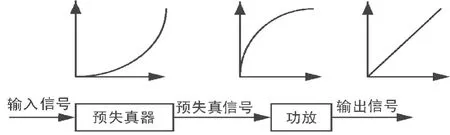
圖1 數字預失真技術的基本原理圖

目前,常用的自適應數字基帶預失真結構主要有2種：①直接學習結構。該結構雖然可以直接更新預失真器的參數,但該結構需要首先辨識功放,對于復雜的功放模型辨識困難;②間接學習結構。該結構不需要辨識功放,對參數的自適應調整可離線完成,并且計算復雜度低,因此該文采用間接學習結構。

2 系統結構

采用間接學習結構的自適應數字基帶預失真系統的結構如圖2所示[2]。

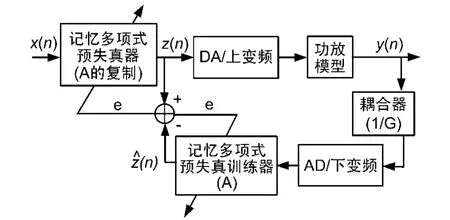
圖2 數字基帶預失真系統框圖

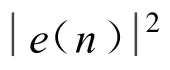
2.1 記憶多項式預失真器

對于有記憶效應的功放,普通的AM/AM和AM/PM函數已經遠遠不能描述該功放的記憶特性和非線性,而Volterra級數以其強大的非線性系統建模能力被廣泛用來對記憶性功放進行建模。Volterra級數的表達式如下：

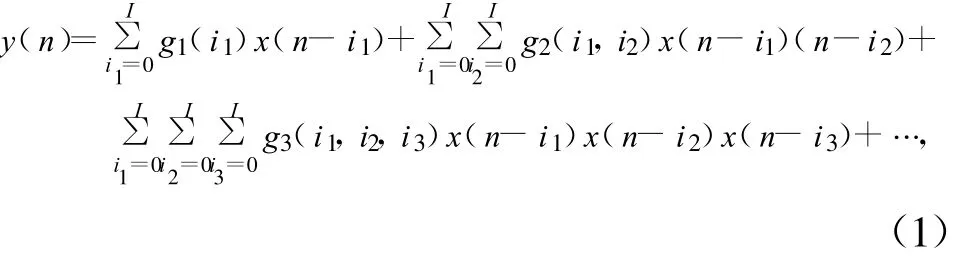
式中,gk(i1,…ik)為K階Volterra核函數,與功放的K階非線性有關,ik為記憶長度。但級數計算復雜,常用的形式是將該級數的核函數除對角線外均為零值,因此簡化為：

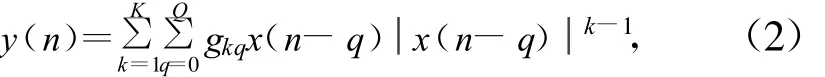
該式很好地表征了功放的記憶性和非線性,而復雜度卻大大降低,稱為記憶多項式。其中K為記憶多項式的階數,Q為記憶長度。由于功放的偶數階非線性對通信系統的影響不是很明顯,因此K通常取奇數[2]。鑒于以上原因,實際中通常取K=5,Q=2。

而預失真器的傳輸函數應當為非線性功放傳輸函數的逆函數,記憶非線性功放模型的逆函數可以用一個記憶多項式來近似,因此預失真器同樣應該用記憶多項式模型：

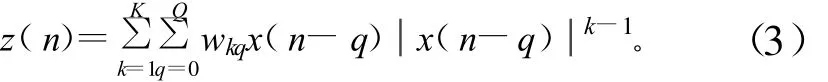
衡量預失真器預失真效果的主要指標就是鄰信道功率比(ACPR)的改善情況,它代表了由于功放非線性所引起的輸出頻譜再生對相鄰頻帶的干擾,定義為鄰信道功率與主信道功率的比值。

2.2 預失真器系數估計算法-RLS算法

RLS算法是一種在數字信號處理中常用的算法,它不僅可以快速收斂,而且能夠通過QR分解等方法來方便地硬件實現,從而避免了大規模的矩陣求逆,節省大量的硬件資源,很適合在預失真系統中使用[3]。

算法流程如圖2所示,定義反饋回路中進入預失真訓練器的信號序列為：

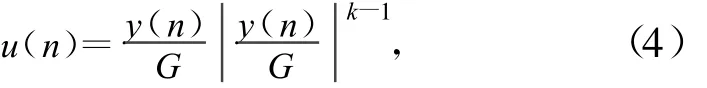
式中,G為功放的增益,而u(n)則為經過衰減進入預失真訓練器(A)的信號。當預失真系統達到收斂時應該有：Z=UW,其中：

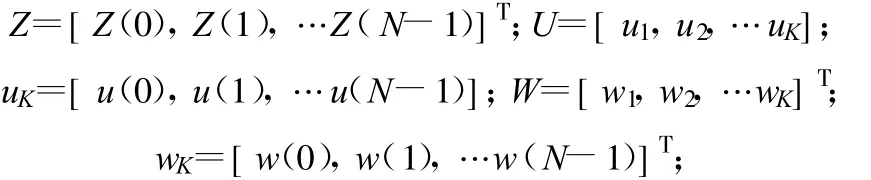
RLS算法迭代過程如下：

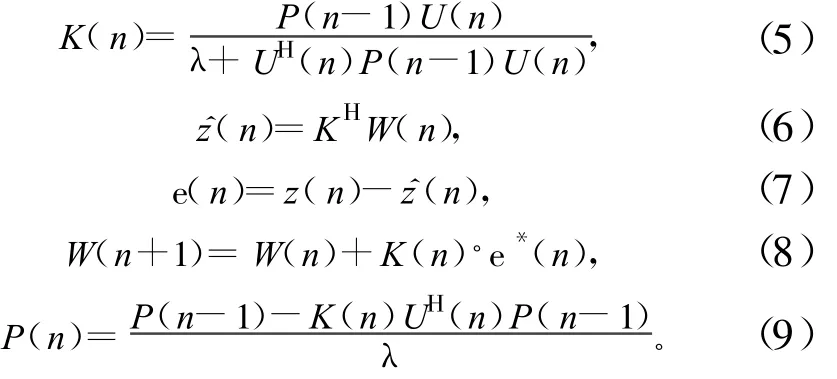
上述式中：(.)*表示共軛,λ為遺忘因子,是一個接近于1,但又小于1的正常數,該文取0.95。

逆矩陣 P(0)=δ-1I,δ為小的正實數,I為單位陣,W=[1,0,…..0]T。

當算法達到收斂時就得到了預失真訓練器(A)的參數,也即得到了預失真器的參數(A的復制)。

2.3 功放模型

功放模型選擇文獻中常用的記憶性功放模型—W-H模型[4],如圖3所示。該模型通過在2個線性濾波器之間級聯一個無記憶非線性系統構成。

圖3 W-H模型功放

其中：

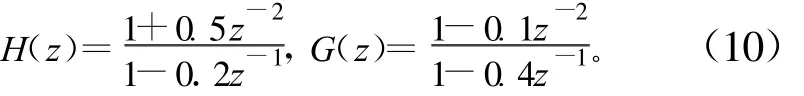
非線性模塊傳遞函數選擇saleh模型：

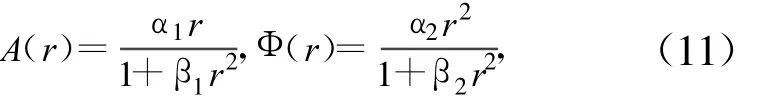
式中：α1=2.158 7,β1=3.151 7,α2=4.003 3,β2=9.104 0。

3 仿真結果分析

仿真中采用16 QAM信號,該信號經過滾降因子為0.25的平方根升余弦濾波器后,再經回退操作(IBO)進入預失真器,而后經過DA/上變頻進入功放(仿真中認為DA/上變頻,AD/下變頻均為理想情況,因此可以忽略)。

IBO為功放的輸入回退,定義為：

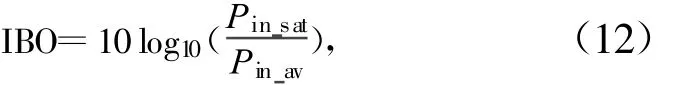
式中,Pin sat 為功率放大器達到飽和時的輸入功率,為平均輸入功率。預失真器采用記憶多項式預失真器,功放采用W-H模型。而IBO=1 dB,以便使輸入信號處在預失真器所能糾正的最大輸入信號范圍內。

從圖4可以看出,經RLS算法預失真后鄰信道功率比(ACPR)比經 LMS算法預失真后改善了約10 dB左右,基本抑制了帶外頻譜擴張。

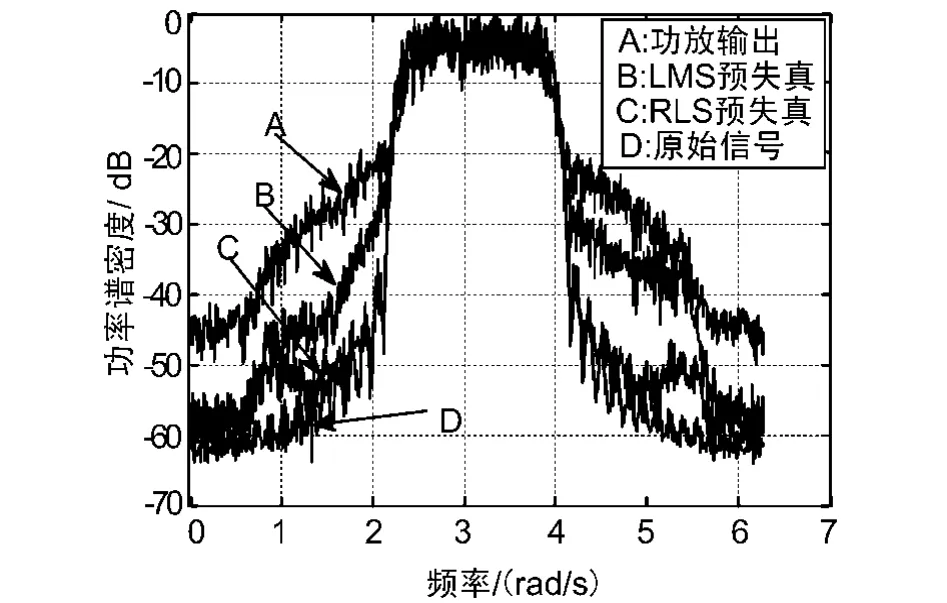
圖4 功放輸出功率譜密度比較圖

圖5為信號經過LMS算法和RLS算法預失真后再經過功放輸出的星座圖,可以看出后者星座圖較前者得到了明顯改善。

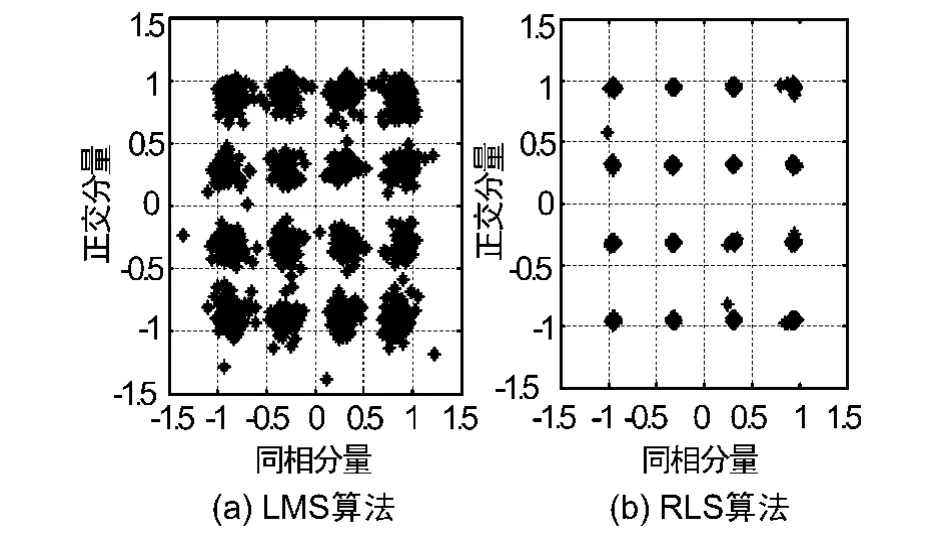
圖5 經LMS、RLS算法預失真后的星座圖比較

從圖6可以看出在未預失真前,因為功放的非線性非常嚴重,誤碼率隨信噪比的增加基本沒有改善,但經過LMS算法、RLS算法預失真后,由于很好地糾正了功放的非線性,所以誤碼率也得到了較好的改善,但RLS算法預失真效果更優(在AWGN信道下)。

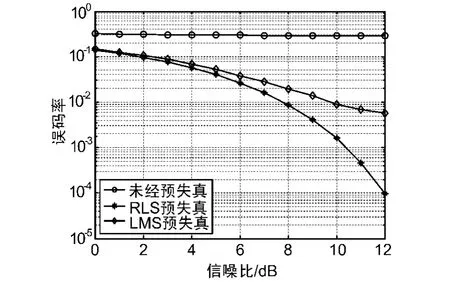
圖6 誤碼率比較曲線圖

而從圖7和圖8的收斂曲線可以看出RLS算法經過300左右次迭代就可以達到收斂(-60 dB),而LMS算法要經過1 600次左右才可以達到相同的收斂效果,因此RLS算法收斂更快,更適合在預失真系統中使用。

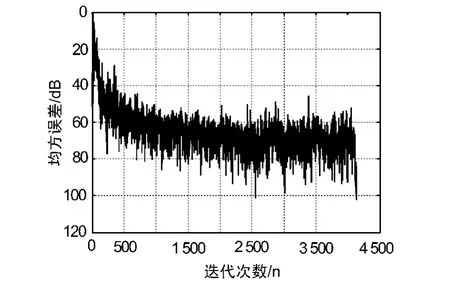
圖7 LMS算法收斂曲線圖

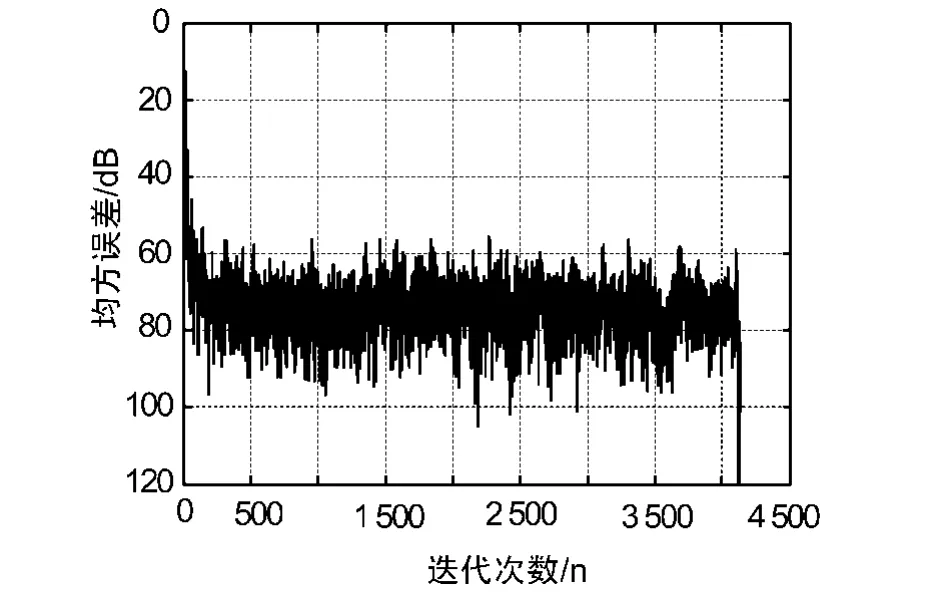
圖8 RLS算法收斂曲線圖

4 結束語

主要介紹了基于RLS算法的記憶多項式預失真技術,經過仿真可以看到預失真后ACPR較LMS算法有10 dB左右的改善,相應的星座圖,誤碼率也得到了很好的改善,并且RLS算法收斂速度很快,預失真性能更優,非常適合在高速通信領域中應用,而在實際的硬件實現中RLS算法可以通過QR分解等方法來輕松實現,節省大量的硬件資源,有很好的工程實踐價值。

[1]沈小虎,金浩,王德苗.射頻功率放大器數字預失真技術及其發展趨勢[J].電信科學,2010(8)：59-65.

[2]DING L,ZHOU G T,MORGAN D R.A robust digital baseband predistorter constructed using memory polynomials[J].IEEE Transactions on Communication,2004,52(1)：159-165.

[3]ZHENG Ning-jing,CHEN Yue-lin,WU Xiao-fang,et al.Digital Predistortion Based on QRD-RLS Algorithm and Its Implementation Using FPGA[C]∥The 1st International Conference on Information Science and Engineering,2010：200-203.

[4]王勇,向新,易克初.基于多項式的記憶型數字基帶失真器[J].西安電子科技大學學報,2006,33(2)：223-226.