衛星通信系統中Chirp信號設計與捕獲
王力男
(中國電子科技集團公司第五十四研究所,河北石家莊050081)
0 引言
在衛星移動通信系統中,頻率同步和定時同步是終端入網的先決條件。一般情況下,窄帶系統中的校頻信道采用Chirp信號,由此來獲得處理增益,而且可使終端同時估計頻率誤差和定時誤差。進行參數設計時應使其頻率變化的范圍覆蓋系統初始的最大頻差,并且應滿足系統的定時精度要求和具有較大的處理增益。
目前查到的Chirp解調方法有2種,即時域匹配頻域判決或者頻域匹配時域判決。無論哪種方法都涉及到判決門限的計算和調整。移動信道存在多徑衰落及多普勒頻移,終端的接收電平和接收信噪比變化較大,采用門限判決比較復雜。該文提出的新方法以信號本身上、下掃頻信號峰值頻率的變化規律作為同步依據,不需要門限,降低了實現的復雜度。
1 Chirp信號參數設計
1.1 Chirp信號參數特點
Chirp信號形式一般表示為
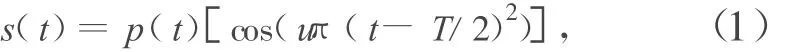
式中,u和T是2個需要確定的參數。易知,u(t-T/2)表示瞬時頻率,由于p(t)是一個(-T/2,T/2)內為1、其余為0的單位矩形脈沖,所以 s(t)的掃頻范圍是(-uT/2,uT/2),信號帶寬等于uT。s(t)信號持續時間長度為T,對整個Chirp信號做匹配相關,可得解調處理增益為uT*T。
1.2 衛星通信系統指標要求
Chirp信號參數值 u、T受系統頻率精度、多普勒頻移等指標約束。以S頻段GEO衛星移動通信系統為例,當衛星存在7°的軌道傾角時,在2GHz上產生的最大多普勒為400 Hz左右;移動用戶車速按200 km/h計算,在2 GHz產生的最大多普勒頻移為370Hz;合計最大多普勒頻移為770 Hz。通信系統也會規定用戶終端鐘源精度,以目前手持用戶終端10 MHz源精度優于5 ppm考慮,在2 GHz產生的頻差為±10 kHz。因此終端初始頻偏在(-11 kHz,11 kHz)內。由于在遮蔽的情況下,信噪比可能比設計門限降低十幾個dB,所以一般系統要求其告警信道在信噪比-10 dB情況下也能正常工作,因此Chirp信號需要有較高的處理增益。
1.3 Chirp信號參數求解
以上述系統參數為例,設定處理增益為21 dB,那么存在一個方程組:

求解方程,可先求出T=0.005 8。在工程實現上,須對T作歸一化,并考慮實現的簡單,設信道符號速率為15.36 kHz,其符號周期為 Ts=1/15 360,則T=90*Ts。進一步求得 u=128/T2=1.42/(90 Ts2),至此Chirp信號參數設計完成。
2 Chirp信號捕獲
2.1 Chirp信號掃頻形式
式(1)也可以表示為:
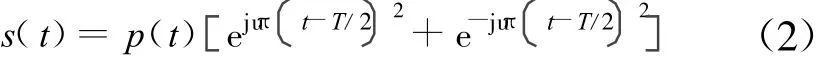
可以看到Chirp信號由上掃頻(即頻率由小向大變化)和下掃頻(即頻率由大向小變化)2種信號合成。假設接收機收到信號為r(t),以ru(t)表示上掃頻,rd(t)表示下掃頻,則 r(t)=ru(t)+rd(t),不考慮噪聲時,ru(t)等于ejuπt+td-T/22×ej2πfdt,rd(t)可表示為e-juπt+td-T/22×ej2πfdt,其中 fd為收發信機之間的頻差、td為本地產生的相關信號與接收信號之間的時間差。
2.2 Chirp信號捕獲原理
接收機對Chirp信號的捕獲框圖如圖1所示,首先,分別用本地上、下掃頻信號和接收信號做相關;然后,對相關后信號進行快速傅里葉變換,求解峰值頻率;最后,根據2個峰值頻率及其變化規律完成定時同步,并求解載波頻差。
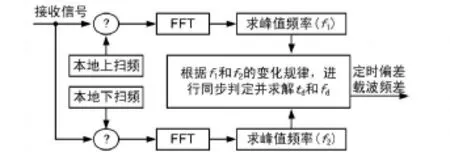
圖1 Chirp信號捕獲原理框圖
本地上掃頻和接收信號相乘,對于接收信號中的上掃頻部分,由于和相乘信號的頻率變化率相同,方向一致,得到一個頻率變化率加倍的掃頻信號,而td和fd產生的影響只是對這個掃頻信號進行了頻譜搬移,做FFT分析時,這部分信號的能量分散在各個頻點上;而對于接收信號中的下掃頻部分,因和相乘信號的頻率變化率相同,方向相反,掃頻部分相抵消,只剩下由 td和 fd產生的單頻信號,做FFT分析時,整個信號功率集中在這個單頻頻點上,很容易求出峰值頻率。根據 rd(t)的表達式,這一路的峰值頻率 f1=fd-utd。
本地下掃頻和接收信號相乘,其過程及分析與上掃頻相似,可得f2=fd+utd。其中 u為已知數。綜合 f1和 f2,從而得到 fd=(f1+f2)/2、td=(f2-f1)/(2*u)。從上述過程看出,準確可靠的求解峰值頻率是Chirp捕獲的關鍵。
在每個FFT計算周期內,總會有頻率最大值,但并不能確定是否有Chirp信號發送,以及本地Chirp信號和接收到Chirp信號的相關程度,所以目前已有的算法多是根據接收條件設定一個門限值,峰值頻率超過這個門限時,認為收到Chirp信號。門限設計既要減少漏檢又要防止虛警;而且為保證接收的動態范圍,門限值可能需要隨信噪比變化而動態調整;并且不同參數的Chirp信號,需要不同的門限。可見門限的設計比較繁瑣,鑒于此,該文提出了一種全新的Chirp信號捕獲方法,該方法從全新的角度出發,根據峰值頻率的變化規律進行捕獲,并不需要門限。
觀察 f1和 f2,其值與 fd、td有關。在Chirp信號持續期間,fd基本不變,f1和f2成為td的線性函數。f1和f2斜率絕對值相同,符號相反,f1單調向下,f2單調向上,在 td=0時,f1和 f2發生交叉。在接收機端設計一個移動觀測窗口,當f1和 f2相等,或f1和f2之間大小發生改變時,認為f1和 f2發生交叉,以此為中心點,觀測其前、后幾對f1和f2是否符合斜率絕對值相同、符號相反的特性,若滿足,則可認為Chirp信號捕獲成功。發生交叉時采樣點可判定為符號最佳采樣點,并根據fd=(f1+f2)/2求出收發信機之間的頻差。
f1和f2發生交叉時,接收到的Chirp信號基本上和本地產生的Chirp信號對齊,Chirp信號能量全部得到利用。發生在交叉前、后的采樣觀測點,收發雖然不完全對齊,其FFT峰值能量損失很小,以不超過整個Chirp長度的1/90計算,損失小于0.1 dB,可以忽略。根據峰值頻率的變化規律來捕獲還可以避免單頻及窄帶干擾對求解峰值頻率帶來的影響。
3 Chirp信號捕獲性能分析
3.1 捕獲概率分析
從圖1可知,接收機用2個支路分別求解上掃頻和下掃頻信號峰值頻率。以掃頻信號考慮,每個支路最后獲得一半的信號功率,相對于總信噪比,支路信噪比降低3 dB。
以第1小節中設計的Chirp信號為例,Chirp信號本身處理增益為21 dB,假設接收機輸入端的S/N為-13 dB,完全相關解調后,得到Chirp信號信噪比為8 dB,每個支路的S/N為5 dB。在5 dB時,求解峰值頻率的錯誤概率為0.88%,2個支路任意一個出錯,就不能滿足捕獲條件,因此求解交叉點的錯誤概率為1.76%。
表1給出了一個MATLAB的仿真統計結果,其輸入信噪比設為為-13 dB,每個符號8倍采樣,仿真次數10 000,捕獲采用第2小節介紹的方法。對于同步誤差列,0表示完全對齊,0.5表示落后半個采樣周期,-0.5表示提前半個采樣周期;統計次數表示10 000次仿真中同一誤差的累計結果。從結果可以看出同步在±1.5樣點內有9 797次,錯誤概率2.03%,采用取舍,±1.5也可以認為是±1。同步誤差在±2.5樣點內有 9 824次,錯誤概率為1.66%,基本符合理論預期。
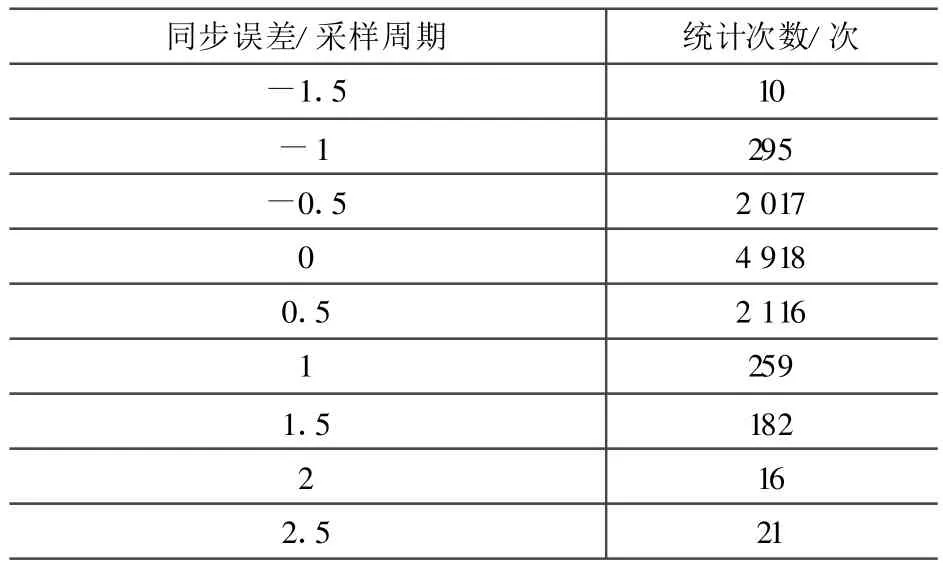
表1 Chirp信號捕獲結果
3.2 頻率精度分析
采用第2小節的捕獲方法,頻率同步和符號定時同步是同時完成的。若只針對Chirp信號長度作FFT運算,則頻率最小分辨率為15.36 kHz/2/90=0.085 3 KHz;為了提高分辨率,可以通過補零的方式擴大FFT的運算點數,相當于擴大了FFT運算周期,運算周期擴大1倍,頻率精度提高1倍。是否需要擴大運算周期同Chirp信號后續信號形式及采用的解調算法有關。
3.3 系統應用性能分析
在衛星通信系統的校頻信道中,Chirp信號周期發送,依據上述設定的條件,用戶連續2次錯誤捕獲的概率為0.017 6%,用戶連續3次錯誤捕獲的概率為0.000 176%。一般來說,移動用戶接收信噪比在-13 dB的情況不多,而且連續3個Chirp周期的持續時間不過0.5 s,不會破壞同步保持,其間用戶還可以解調基本告警信道來進行同步跟蹤。
在某些衛星通信系統中,有終端突發工作模式,用于傳送數據信號,信號形式是Chirp信號加上有長度限制、帶幀格式的編碼調制信號。數據信號解調有最低門限信噪比要求,低于此門限就不能保證誤碼率及誤幀率。假定數據解調門限為-2 dB,Chirp信號解調后S/N為19 dB,每個支路的S/N為16 dB,如此高的信噪比下,可認為Chirp信號能夠完全正確解調。
4 結束語
根據峰值頻率斜線交叉特點判定Chirp信號同步,避免了判決門限的使用,尤其適用于移動通信。以交叉點來判定,不需換算,定時同步更為準確,算法實現更為簡單、可靠。該方法已在某系統中得到使用,實際性能和理論分析一致,誤差估計準確,滿足系統要求。
[1]VISHWANATH TG,PARRM,SHIZL,etal.Synchronization in mobile satellite systems using dual-Chirp waveform[P].United States Patent:US 6,418,158 B1,Jul.9,2002.
[2]SUN Y T,LIN J C.Estimation of timing delay andfrequency offset using a dual-Chirp sequence[C]∥.Wireless VITAE 2009,2009:18-21.
[3][美]斯克拉.數字通信—基礎與應用(第2版)[M].徐平平 譯.北京:電子工業出版社,2002.

