平板電容器邊緣電場特性探究

邵小桃,成 超,張靜文

(北京交通大學 電子信息工程學院,北京 100044)

平板電容器是“電磁場與電磁波”課程中靜態場部分常見的計算模型。根據平板電容器的電荷分布,可以計算平板電容器的電位和電場分布。為了求解方便,一般情況下將平板導體上的電荷分布視作均勻的,基于Schwarz-Christoffel變換,仿真求解平板電容器電場和電位分布。在實際情況下,平板導體上電荷分布并不是均勻的。本文討論線電荷密度為ρ的帶電長線在相距為r的點處產生的電位,然后利用Matlab仿真軟件,得出平板電容器上的電荷密度分布,最終給出空間電位分布和電場分布仿真圖形。從結果可以看出,平行板平均分塊數N越大,所得出的結果越逼近實際情況。

1 均勻帶電長條的電位分布

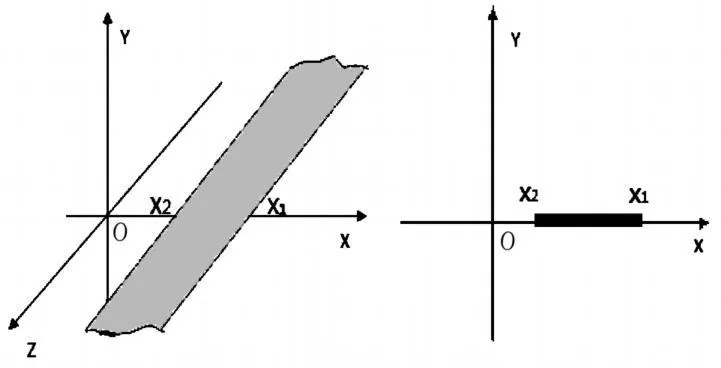
圖1 xoz平面中的均勻帶電長條

沿 x2到 x1方向,電荷均勻分布,此時每一線元dx實際代表與z軸平行的帶電長線。如選取有限足夠遠r0處為參考點,線電荷密度為ρ的帶電長線在軸距為r處產生的電位:

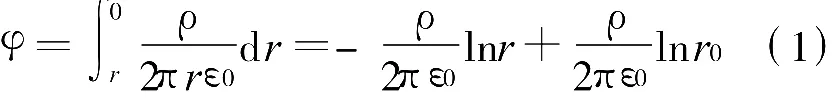
寬度在x2到x1的帶電長條可看做無限多個線電荷密度為ρ的帶電長線構成,每個帶電長線在二維平面中的點(x,y)處產生的電位

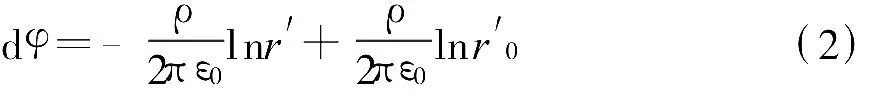
因為r0選在有限足夠遠,則x對r′0無影響,可看作常數。此處僅討論等位線,可將上式積分常數項舍去,故有

寬度在x2到 x1的帶電長條在二維平面中的點(x,y)處產生的電位為

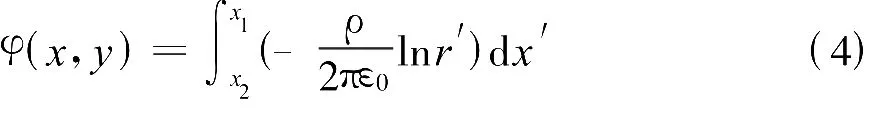
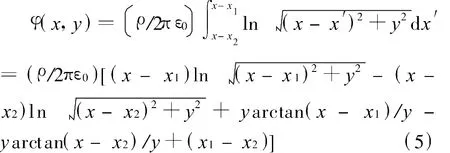
其等位線如圖2所示。

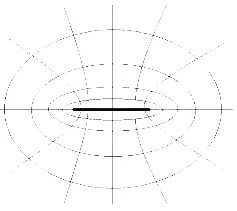
圖2 均勻帶電長條的電位分布

從圖2可以看出,等位線為橢圓簇;電場線在導體表面有切向分量,切向分量沿邊緣方向越來越大,并致邊緣完全達到切向。電場線在導體表面有較強的切向分量,將促使導體內部自由電荷向導體兩端移動,直至電荷分布使得其產生的電位滿足導體為等位體,否則電荷將在切向電場的作用下繼續移動。最終,電荷分布將呈現出兩端多,中間少的情形。這就是平行板的“邊緣效應”。

2 平板電容器電場分布逼近

依據上面討論,將實際將實際平板電容器沿z向無限延伸,而 x方向則有限延伸,將三維問題轉換成為二維問題。xoy平面內相距為d、寬度為a的平板電容器如圖3所示放置。

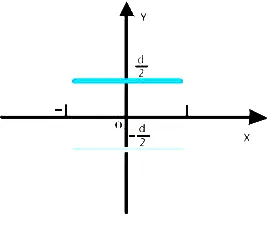
圖3 平板電容器xoy平面圖

依據前面推導出的公式,對應圖3可寫出中點位于(0,0)處、長為a的均勻帶電長條在點(x,y)處產生的電位

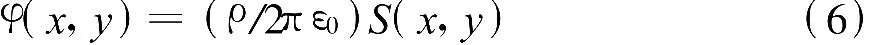
其中,有

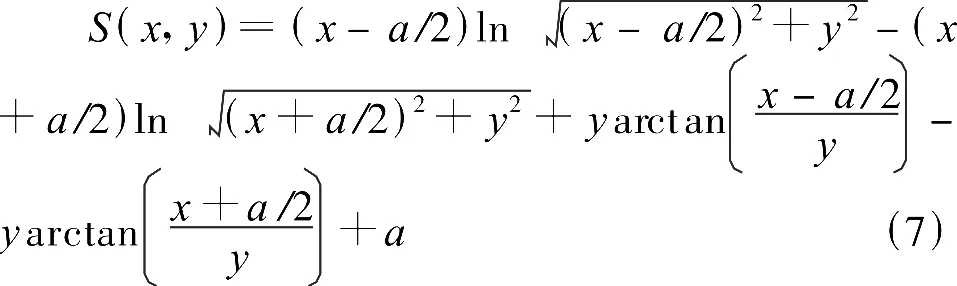
那么,當長條中心位于(X,Y)處時,其在(x,y)點出激發的電位為

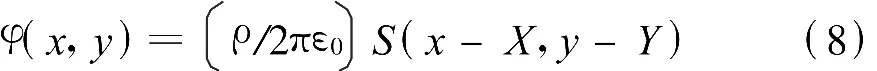
從上式可以看出,平行板電容器的空間電位分布與板上的電荷密度有關,由于數學表達式復雜,直接求解存在一定的難度。此處采用逼近思想,間接求出平板電容器極板上的電荷分布。

將平行板平均分為2N塊窄長條,上下各為N塊,如圖記作1,2,…,2N-1,2N號。每塊窄長條帶電均勻,且電荷密度分別為ρ(1),ρ(2),…,ρ(2N-1),ρ(2N)。

由對稱性知:

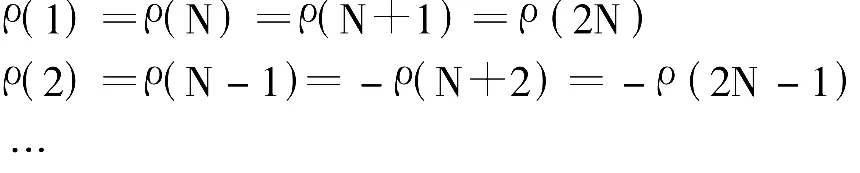
xoy平面內任意一點(x,y)處的電位為2N個窄長條在此處產生電位的疊加,表示為

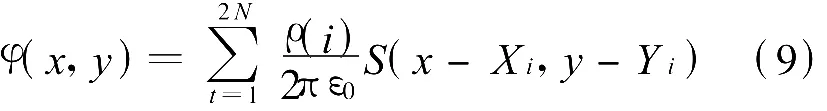
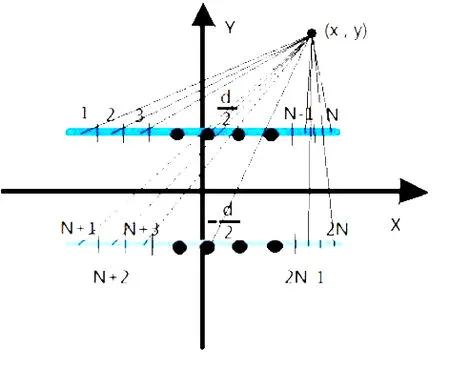
圖4 平板電容器在xoy平面產生的電位

如果利用vi表示第i塊長條中心點處的電位,由上式則有

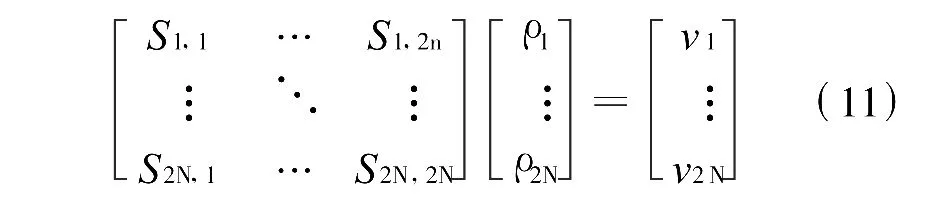
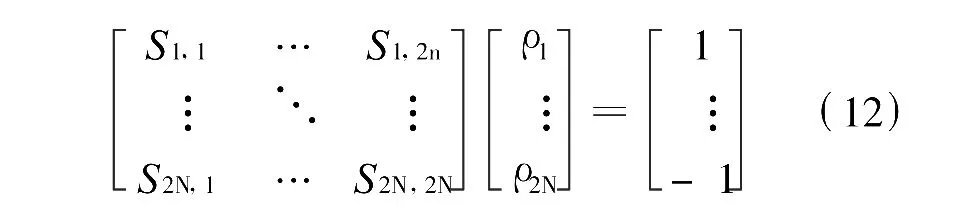
利用上式,可由計算機求出電荷密度σ數組,這樣由式

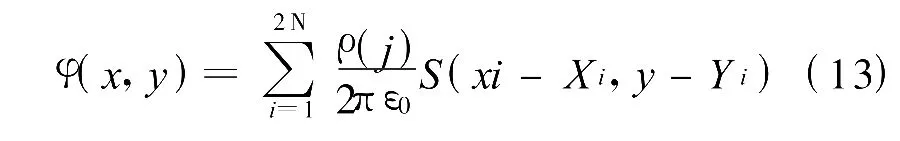
可得出空間電位分布,利用式 E(x,y)=-φ(x,y),也可以得到空間電場分布。

利用Matlab仿真可以計算,N=10時的電荷密度分布ρ,如圖5(a)所示。此處只給出極板N=10個長條分別對應的電荷密度大小。

當N=100時,計算出的ρ如圖5(b)所示。

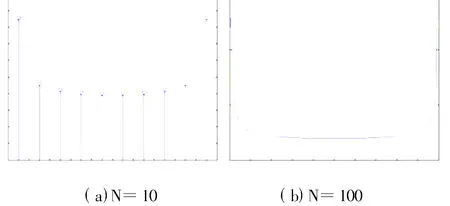
圖5 不同N時平板電容器電荷密度分布

從圖5可以看出,平板電容器極板上的電荷密度呈現兩端多,中間少的分布情形,即平板電容器的“邊緣效應”。且N越大,所得出的結果越逼近實際情況。利用quiver函數,可以得到對應電位的電場分布。N=20時電位和電場分布的Matlab仿真圖形如圖6所示。

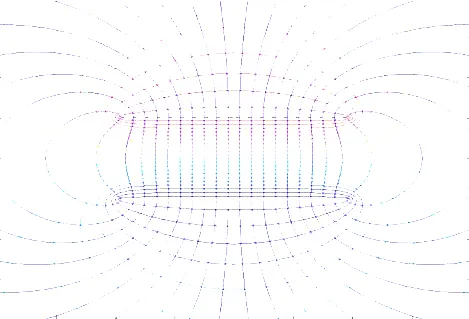
圖6 平板電容器電位和電場連續分布的Matlab仿真

可見,導體表面電場線仍然垂直于導體表面,但在無限大的空間,呈現的則是曲線。

3 結語

考慮邊緣效應的平板電容器電場和電位場分布逼近法,并沒有推導出嚴格的電荷分布函數,但是卻適應于任何形狀的導體電荷密度的近似求解。只要得到電荷密度,電位、電場分布也就迎刃而解。將此結果與通過S-C變換得到的理論值的仿真結果作比較,結果非常吻合,說明此逼近方法切實可行。

[1] H A 豪斯、J R 梅爾徹.電磁場與電磁能[M].美國,麻省理工大學,1989

[2] 邱萬英.非理想邊緣電容器電容的分析[J].南昌:華東交通大學學報.2008,(25).

[3] 龍非池、王慧.基于Schwarz—Christoffel變換的平板電容器電場點和分布仿真[J].北京:物理與工程.2007,(17).

[4] 謝處方.電磁場與電磁波[M].北京 :高等教育版社,2006