土體應變軟化對盾構掘進面穩定性的影響

張義同，袁 杰

（天津大學 機械工程學院力學系，天津300072）

在地鐵盾構施工中，施工事故時有發生，其中社會影響較大的事故是由掘進面失穩引發地表沉降導致地表坍塌造成的[1]。影響掘進面穩定性的因素很多，土體的應變軟化可能引起隧道掘進面失穩，但在隧道開挖面穩定性分析中還很少考慮應變軟化的影響。早在20世紀60年代，人們就開始關注土體的應變軟化行為，Skempton在研究邊坡的穩定性時就指出了，具有應變軟化性質土坡與具有應變硬化性質土坡的漸進破壞過程不同，應變軟化對邊坡的穩定具有重要影響[2－3]；張嘎基于瑞典條分法的基本原理，提出了一個能考慮土的抗剪能力與剪應變關系的應變軟化邊坡穩定性簡化評價方法，研究了土的應變軟化特性對邊坡穩定性的影響[4]。Brown較早地考慮了涉及應變軟化時隧道圍巖穩定性分析的理論問題，但沒有考慮塑性區彈性應變的變化，得到的結果存在較大誤差[5]；Lee和Pietruszczak對隧道圍巖的應變軟化進行分析，采用了有限差分法求解平衡方程與協調方程，得到了隧道圍巖的塑性區與彈性區的分布范圍[6]。于學馥利用材料的參數從彈塑性界面向隧道壁減小來考慮材料軟化，分析了隧道圍巖的穩定性[7]；王星華則采用彈性 塑性軟化 塑性殘余三線性應力 應變模型推導了隧道圍巖的彈塑性區半徑、圍巖應力的解析表達式，分析表明應變軟化對圍巖穩定產生不利的影響[8]。

研究表明，應變局部化是應變軟化材料的一種失穩現象[9]。應變局部化的變形往往集中在一個很狹窄的帶狀區域內，也稱為剪切帶。目前已有一些文獻對土體剪切帶進行了研究[10－14]，在理論研究中，一般把應變局部化看成是一個分岔問題[14－15]，Zhang[9]進一步指出，其穩定的分岔解是一個兩相解，用一般的分岔分析方法求出的是單相解，難以求出其穩定的分岔解，并通過相變分析，給出了土體平面應變下剪切帶的解析解。盾構掘進面的失穩是三維問題，對其進行解析分析是比較困難的，采用數值模擬方法對盾構掘進面的穩定性進行分析，對比土體是否考慮應變軟化的情況，得出應變軟化對掘進面穩定產生的影響。

1 數值分析的可靠性驗證

首先介紹利用相變理論對Alshibli和Sture[10]實驗中砂土剪切帶的解析分析，再利用數值方法對剪切帶的形成與擴展進行數值模擬，將模擬結果分別與解析解和實驗結果進行比較，來檢驗本文數值方法的正確性。

1.1 基于兩相平衡理論的剪切帶解析解

Abeyaratne[16]和 Zhang等[9]以具有應變軟化行為的一維彈塑性桿為例，說明了在均勻拉伸的過程中可能存在的兩個分岔解：一個是傳統的單相均勻變形解，另一個是兩相解。并指出兩相解的應變能最小，是穩定的分岔解。Fu[17]和Zhang等[9]建立了應變局部化的兩相平衡模型，剪切帶內區域是高應變相（塑性相），剪切帶以外的區域是低應變相（彈性相），在每一相內，必須滿足平衡方程（不考慮體積力）：

式中：div為散度算子；π為第一Piola－Kirchhoff應力張量；T表示張量的轉置。

相變界面處的Eshelby力和位移是連續的，應變梯度和應力是不連續的，跨越相變界面的跳躍應滿足：

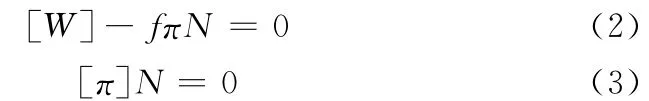
土體剪切帶的變形是非均勻變形，可以將剪切帶內和剪切帶外的變形看作是分片均勻變形，于是各相域內的平衡方程自然滿足，由（2）、（3）式可得到平面應變狀態下砂土剪切帶的控制方程，解控制方程與＝1組成的方程組可求出剪切帶出現時的臨界應力、剪切帶的法線方向矢量、剪切帶內和剪切帶外的變形等。Zhang等[9]對 Alshibli和Sture實驗中F4砂土剪切帶的解析分析的臨界應力和剪切帶傾角列于表2中。

1.2 平面應變條件下砂土剪切帶的數值模擬

采用有限差分法程序FLAC3D進行數值分析，本構模型取為Mohr－Coulomb應變軟化模型，材料塑性屈服后，粘聚力、摩擦角、剪脹角發生應變軟化，把這些變量作為塑性應變的函數。試件使用Alshibli和Sture實驗中的F4砂土，其材料參數如表1所示。

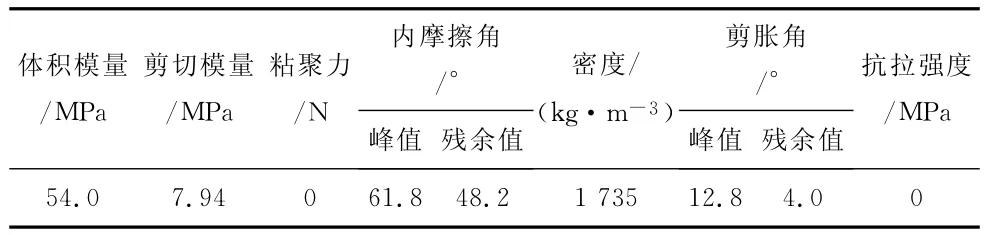
表1 F4砂土材料參數

砂土試樣寬0.15m，高0.3m，厚0.02m，共劃分900個單元，為了激發局部變形的產生，在試樣中引入缺陷單元。邊界條件如下：在試樣上下兩端施加常速率1.5×10－6m／時步以控制位移，左右兩側施加15kPa圍壓，前后兩側約束位移。數值模擬出砂土試樣的變形情況如圖1所示，變形從缺陷點啟動，缺陷點及其相鄰單元中的應力與應變關系表現為應變軟化，而遠離缺陷點的單元還處于彈性狀態，變形充分發展后，集中于局部區域并沿局部區域迅速擴展，形成了一條明顯的剪切帶（圖1（c）），圖2為Alshibli和Sture實驗的剪切帶照片。通過查網格法計算出圖1中剪切帶的切向與水平方向的夾角為57.9°，剪切帶形成時的臨界應力為177kPa，與解析分析的臨界應力172.056kPa比較接近，也在上屈服極限239.25kPa之下，與實驗觀測的結果一致，在上屈服極限就要到達之前，剪切帶就出現了。剪切帶的實驗結果、解析解和數值模擬結果對比情況如表2所示，數值模擬的剪切帶傾與實驗測得的剪切帶傾角相吻合，誤差僅為5.3%，與解析分析的剪切帶傾角誤差也僅為4.8%，說明了用本文的數值方法來模擬應變軟化土體的變形是可行的。

圖1 剪切應變增量發展云圖

圖2 實驗中剪切帶的照片

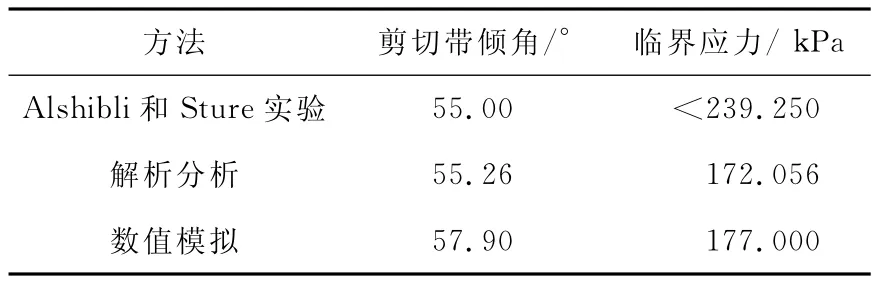
表2 剪切帶的數值模擬結果與實驗結果和解析解的對比

2 考慮土體應變軟化的盾構掘進面穩定性分析

開挖隧道是一個逐漸推進的過程，考慮到分析的重點是土體應變軟化對掘進面穩定性的影響，因此忽略注漿壓力、注漿厚度等因素的影響。數值模擬時一次性開挖隧道一定距離，并及時設置襯砌管片，同時在開挖面上施加大小與原始地層側向靜止土壓力值相等的梯形支護作用力，地層水平側向土壓力為垂直壓力乘以側壓力系數，側向壓力系數取值0.5。為了方便描述，取隧道中心點支護壓力值來代表開挖面支護壓力大小，支護壓力開挖面中心點施加的支護壓力，p0為中心點原始地層的水平靜止土壓力之比。

2.1 計算模型及本構關系

隧道計算模型如圖3所示。模型總長度100m，寬度50m，總高度65m，隧道直徑為10m，隧道埋深20m，隧道已開挖50m。模型的坐標如下：y軸沿隧道軸線，z軸垂直于地面。考慮到土體模型對稱性，對其一半進行網格剖分。其邊界約束條件為：1）地表面為自由面；2）四周限制水平位移，底部限制豎向位移。假定地下水位與地表一致，土體材料為砂土，考慮砂土應變軟化時采用Mohr－Coulomb應變軟化模型，不考慮砂土應變軟化時采用Mohr－Coulomb模型，砂土參數如表3所示，管片材料為C50彈性鋼筋混凝土結構，厚度為35cm，采用shell單元模擬。

圖3 隧道計算模型

表3 土體材料參數

2.2 計算結果與分析

2.2.1 不考慮滲流時土體應變軟化與不軟化的對比 當開挖面支護壓力小于地層原始地應力時，引起土體應力釋放，導致掘進面土體變形。不考慮滲流時掘進面上中心點的水平位移與支護壓力比的關系如圖4（a）所示，隨著支護壓力比不斷減小，開挖面中心點的水平位移量逐漸增大，當支護壓力比減小到一定程度時，中心點的水平位移量有一個突變，之后位移急劇增大，在支護應力幾乎不變的情況下變形還會繼續發展。根據穩定性理論，把開挖面支護壓力的微小變化導致開挖面中心點水平位移突變時的支護壓力定為極限支護壓力，相應的支護壓力比稱為極限支護壓力比。由圖可知，考慮砂土應變軟化時的極限支護壓力比為0.2，大于不考慮軟化時的極限支護壓力比0.1，相應的考慮軟化時的極限支護壓力也大于不考慮軟化的極限支護壓力。

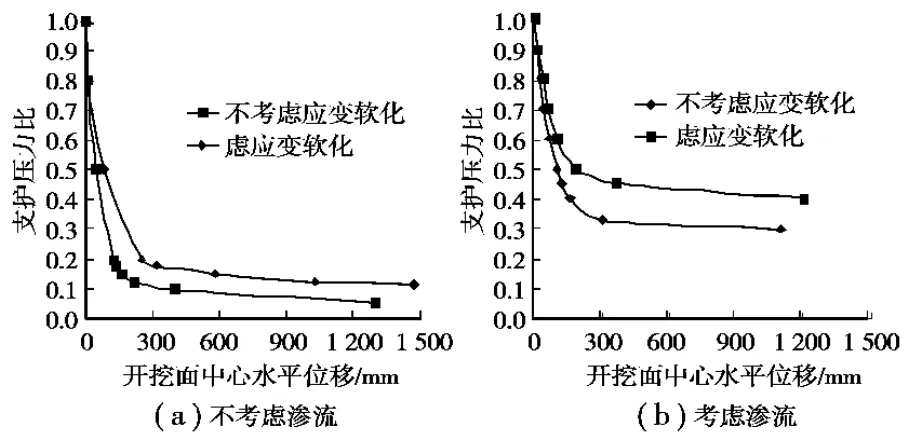
圖4 支護壓力比和開挖面中心的水平位移關系

2.2.2 考慮滲流時土體應變軟化與不軟化的對比 由圖4（b）可以看出，考慮滲流及土體應變軟化時的極限支護壓力比為0.45，也大于考慮滲流但不考慮應變軟化時的極限支護壓力比0.32，土體的應變軟化可以使掘進面的極限支護壓力變大。與圖4（a）相比可知，滲流對掘進面穩定性的影響也比較大，因此，在有地下水存在的情況下不可忽略滲流作用的影響。

支護壓力比同取0.45時，滲流情況下Z向（垂直地面方向）的位移云圖見圖5，不考慮應變軟化時，僅在掘進面附近的位移值較大，地表面的Z向位移即地表沉降還不是很大；考慮應變軟化時，位移較大的區域已經從掘進面處擴展到地表面附近，在開挖面前方形成一個“漏斗”狀，兩者的塑性區發展情況見圖6。

圖5 Z向位移云圖

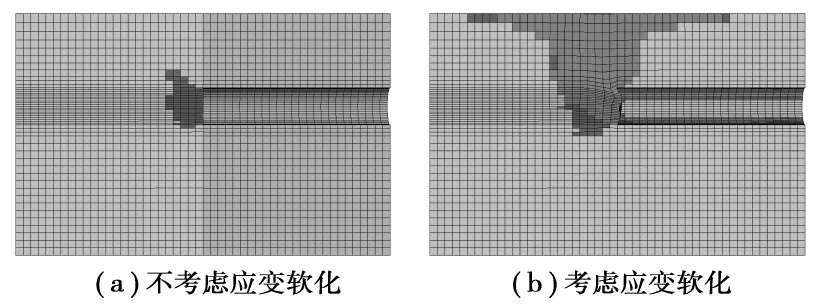
圖6 土體的塑性區云圖

從圖6可以看出，兩者的塑性區擴展范圍差別很大，不考慮砂土應變軟化時塑性區雖然得以擴展，但擴展范圍還比較小，還沒有發展到地表面；而考慮應變軟化時，掘進面前方土體的塑性區已迅速大范圍擴展，并與地面貫通，引起地表產生較大的變形。地表沉降情況如圖7所示，其中（a）是掘進面正上方地面沿x方向（垂直隧道軸線方向）的沉降曲線，（b）為隧道正上方沿y方向（隧道軸線方向）的地表沉降曲線，開挖方向沿坐標軸正向，開挖面位于橫坐標原點處。由圖可知，考慮到土體的軟化時，隧道正上方地表已經下沉140mm見圖7（a），地表的最大沉降出現在開挖面前方，其值為200mm見圖7（b），此時地表已塌陷；而不考慮軟化時，最大地表沉降僅為12mm。從圖還可以看出，土體應變軟化對掘進面上方地表附近的沉降影響很大，對遠離掘進面的地表影響較小。

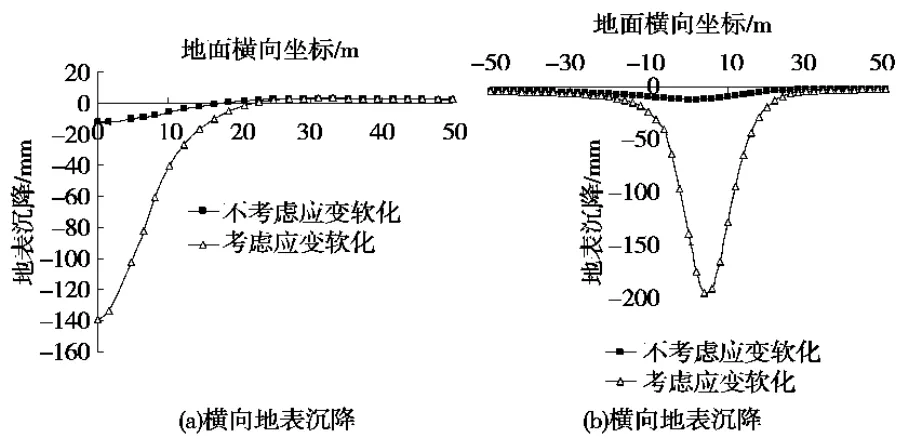
圖7 地表沉降曲線

由以上對分析可知，土體的應變軟化對盾構隧道掘進面的穩定性影響非常大，隨著盾構掘進的進行，由于開挖面支撐處理不當，具有應變軟化特性的土層會逐漸因局部區域的變形急劇發展而加快盾構掘進面的失穩，導致較大的地面沉降變形，嚴重時導致隧道坍塌。而且這種局部化變形的發展有時會很突然，沒有任何警示的跡象。所以，在隧道工程中，遇到具有應變軟化的特性的地質，必須考慮應變軟化對掘進面穩定性的影響，從而在施工中采取合理的支護方法，預防隧道土體坍塌事故的發生。

2.2.3 砂土不同應變軟化行為對掘進面穩定性的影響 砂土的軟化參數剪脹角和內摩擦角取值見表4，圖8（a）為不同方案剪脹角的支護壓力比與開挖面最大水平位移曲線，隨著剪脹角峰值的減小，開挖面極限支護壓力比逐漸增大。圖8（b）為不同方案內摩擦角的支護壓力比與開挖面最大水平位移曲線，隨著內摩擦角峰值的減小，極限支護壓力比也逐漸增大，相比較而言，內摩擦角的變化對掘進面穩定性的影響較大。

表4 不同方案的剪脹角與內摩擦角

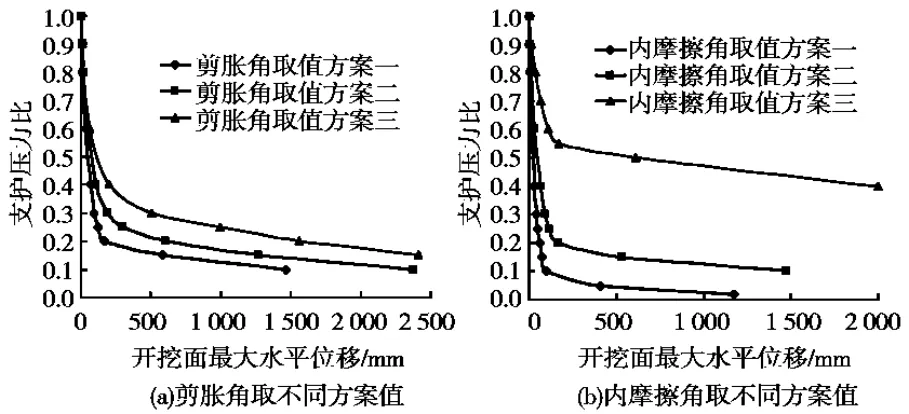
圖8 支護壓力比與開挖面最大水平位移關系

3 工程實例分析

3.1 工程概況

在天津地鐵九號線十一經路站到大直沽西路站區間，采用小松公司的TM634PMX土壓平衡盾構機，刀盤直徑6.32m，隧道襯砌采用35cm厚的C50混凝土管片，管片環寬1.2m。此區間地質構造復雜，地層復雜多變，其中500～600環的地質剖面圖見圖9，土層有填土、粘土、粉質粘土、粉土、粉砂。隧道從中部較厚的粉質粘土層穿過，其埋深為14.1～14.5m。

圖9 地質剖面圖

3.2 計算模型

由于FLAC3D前處理功能較弱，為了建立隧道的有限差分模型，先通過AutoCAD建立三維模型，然后利用ANSYS對模型進行網格劃分，最后通過轉換程序將模型導入FLAC3D中，從而實現快速建立復雜三維地質模型（圖10），模型長120m，寬30m，高度取35.5m，隧道直徑6.32m，埋深取平均值14.3m。邊界條件為：模型側面和底面為位移邊界，側面限制水平位移；底部為固定邊界，限制水平移動和垂直位移；模型上面為地表面，為自由邊界。土體的本構模型采用Mohr－Coulomb應變軟化模型，由于有地下水的存在，同時采用水土耦合計算，考慮了滲流作用。各土層的主要物理參數見表5，襯砌管片的密度為2 450kg／m3，彈性模量為34 500MPa，泊松比為0.17。

圖10 計算模型

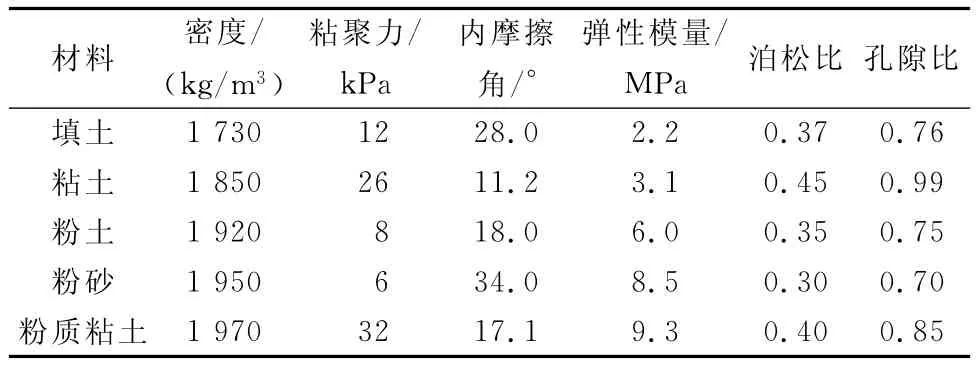
表5 土層的參數

3.3 計算結果及分析

盾構施工引起的地表沉降因素眾多，其中開挖面前方土體的沉降或隆起大小與開挖面支護壓力的大小密切相關。若支護壓力過大，造成掘進面前方地表的隆起；若支護壓力過小，引起前方地表沉陷，嚴重時會引起地表坍塌。圖11給出了開挖10m、20m、50m、80m、90m時不同支護壓力比下的地表縱向 （沿隧道軸線方向）沉降曲線，開挖方向沿橫坐標軸負向。

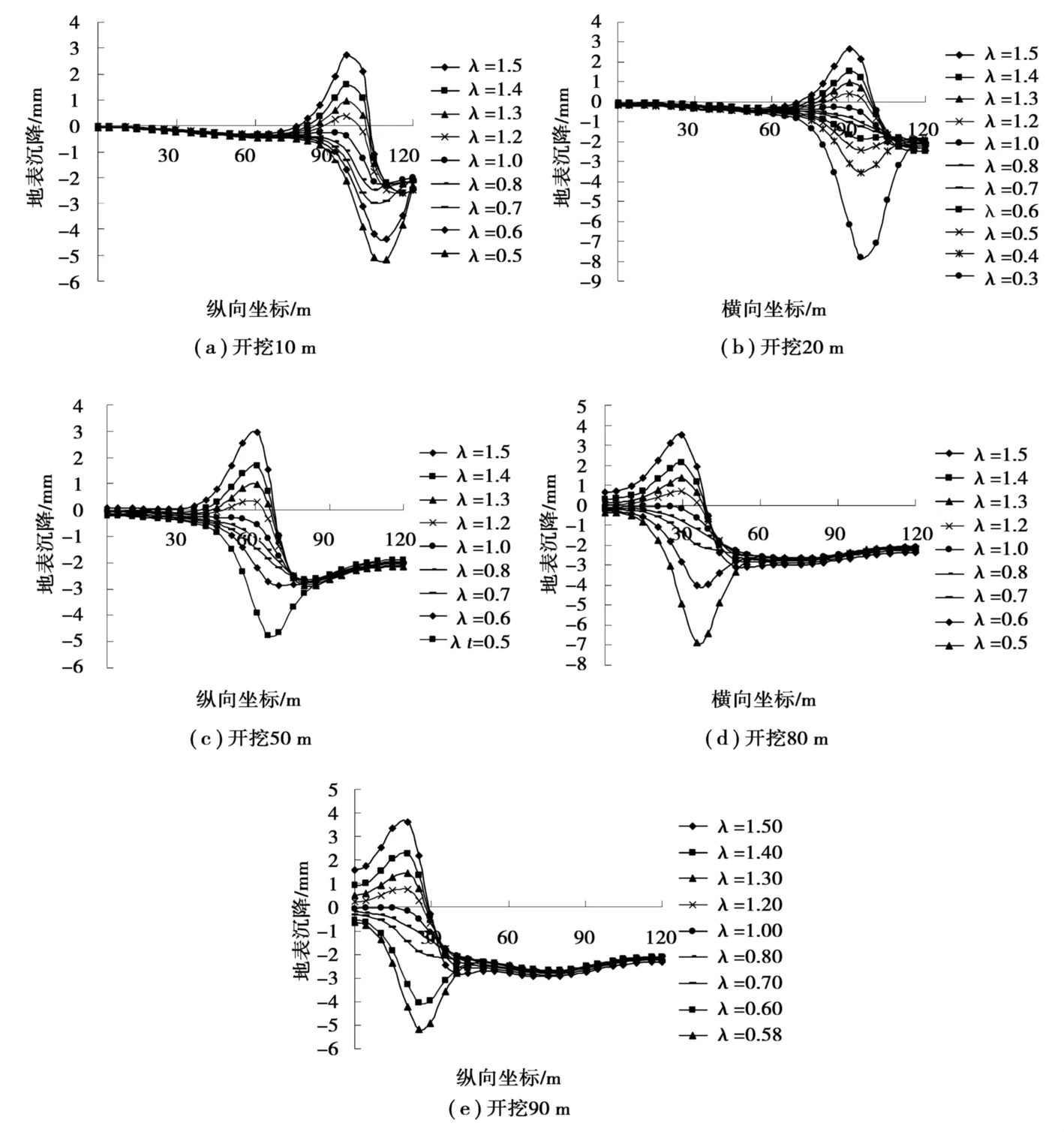
圖11 不同支護壓力比下的地表縱向沉降曲線

從圖11可以看出，開挖面支護壓力比由1.0逐漸減小時將會引起開挖面前方地表一定距離內沉降變形越來越大，最大沉降點發生在開挖面前方5m左右，接近隧道直徑6.32m；支護壓力比逐漸增大時，開挖面前方地表的隆起量會越大越大，最大隆起點則在開挖面前方大約10m處。開挖10m時，支護壓力比為0.7的開挖面前方地表最大沉降值為2.90mm，0.6時最大沉降值達到4.38mm（圖11（a））。由于天津地鐵九號線要穿越城市中心地帶，地面建筑物密集、地下管網密布等，因而施工中對地表的控制要求較為嚴格，要求盾構掘進時開挖面前方地表沉降不超過3mm，以及隆起量控制在2～3mm。根據要求由圖11可得出，開挖10m、20m、50m、80m、90m時掘進面合理支護壓力比范圍分別為0.6～1.4、0.5～1.4、0.6～1.4、0.7～1.3、0.65～1.3，各開挖面土層原始側向土壓力分別為0.23MPa、0.23MPa、0.22MPa、0.25MPa、0.24MPa，從而得出合理的支護 壓 力 范 圍 分 別 是 0.092～0.322MPa、0.132～0.308MPa、0.175～0.325MPa。

3.4 與監測數據的比較

在盾構施工過程中，土倉壓力左右測點分布如圖12所示，圖13中脈沖式的波動曲線給出了500～600環區間左右測點的土壓監測值，并根據上文預測的范圍給出了支護壓力的上下限，理想支護壓力為開挖面原始側向土壓力。監測的土壓力值在理想支護壓力附近波動，波動的范圍與預測的范圍基本一致，說明了分析預測的支護壓力范圍是合理的，考慮土體軟化時對隧道掘進面土體變形分析是比較準確的，如果忽略土體的應變軟化行為則偏于危險。

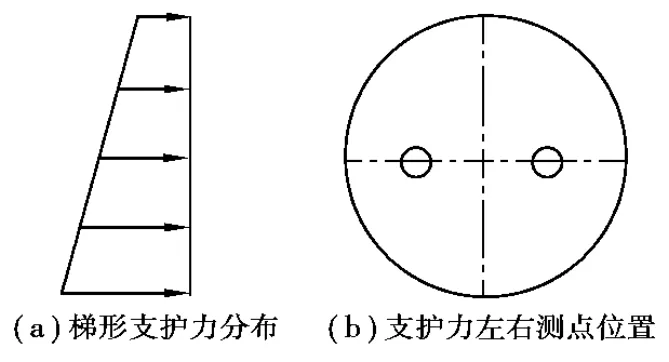
圖12 支護力分布與測點位置圖

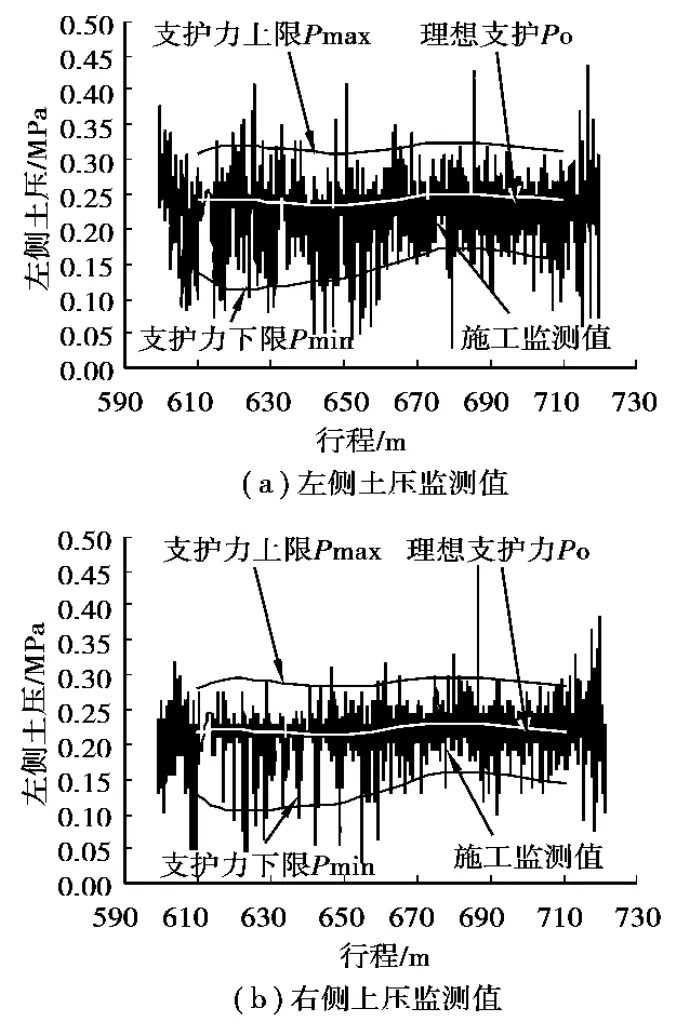
圖13 土壓監測值

4 結 論

通過數值模擬分析，并以工程實例進行了驗證，得到以下結果：

1）土體的應變軟化可以加快土體塑性區的擴展，使土層及地表的變形加劇，掘進面的極限支護壓力也增大，更容易引起掘進面失穩并導致隧道坍塌。

2）不同剪脹角和內摩擦角的應變軟化行為對掘進面穩定性的影響會不同，其中內摩擦角的影響更顯著。

3）在工程實例分析中，考慮了土體的應變軟化和地下水的滲流，預測了施工中的支護壓力，預測的范圍與實際監測的土倉壓力波動范圍基本吻合，得到了工程的驗證。這為我國目前正大規模進行的隧道工程建設的設計與施工提供依據，對于掘進面的穩定性控制具有重要的現實意義。

[1]劉輝，張智超，王林娟.2004－2008年我國隧道施工事故統計分析[J].中國安全科學學報，2010，20（1）：96－100.LIU HUI，ZHANG ZHI－CHAO，WANG LIN－JUAN.Statistical analysis on safety accidents of tunnel construction from 2004 to 2008in China[J].China Safety Science Journal，2010，20（1）：96－100.

[2]SKEMPTON A W.Long－term stability of clay slopes [J].Geotechnique，1964，14（1）：77－101.

[3]SKEMPTON A W.Residual strength of clay in landslide，fol－ded strata and the laboratory test[J].Geotechnique，1985，35（1）：1－18.

[4]張嘎，張建民.基于瑞典條分法的應變軟化邊坡穩定性評價方法[J].巖土力學，2007，28（1）：12－16.ZHANG GA，ZHANG JIAN－MIN.Stability evaluation of strain－softening slope based on Swedish slice method[J].Rock and Soil Mechanics，2007，28（1）：12－16.

[5]BROWN E T，BRAY J W，LADANYI B，et al.Ground response curves for rock tunnel[J].Journal of Geotechnical Engineering，1983，109：15－39.

[6]LEE Y K，PIETRUSZCZAK S.A new numerical procedure for elasto－plastic analysis of a circular opening excavated in a strainsoftening rock mass [J].Tunneling and Underground Space Technology，2008，（23）：588－599.

[7]于學馥，等.地下工程圍巖穩定性分析[M].北京：煤炭工業出版社，1983.

[8]王星華，章敏，王隨新.考慮滲流及軟化的海底隧道圍巖彈塑性分析[J].巖土力學，2009，30（11）：3267－3272.WANG XING－HUA，ZHANG MIN，WANG SUI－XIN.Elastoplastic analysis of surrounding rocks of subsea tunnel with consideration of seepage and material softening[J].Rock and Soil Mechanics，2009，30（11）：3267－3272.

[9]ZHANG YI－TONG，Qi DE－XUAN，DU RU－XU，et al.Prediction of shear bands in sand based on granular flow model and two－phase equilibrium [J].Journal of Central South University Technology，2008，15（s1）：316－321.

[10]ALSHIBLI K A，STURE S.Shear band formation in plane strain experiments of sand [J].Journal of Geotechnical and Geoenvironmental Engineering，2000，126（6）：495－503.

[11]HUANG M S，LU X L，QIAN J G.Non－coaxial elasto－plasticity model and bifurcation of shear banding in sands[J].International Journal for Numerical and Analytical Methods in Geomechanics，2010，34（9）：906－919.

[12]ROSCOE K H.The influence of strains in soil mechanics[J].Geotechnique，1970，20（2）：129－170.

[13]ARTHUR J F R，DUNSTAN T，AL－ANI Q A J，et al.Plastic deformation and failure in granular media[J].Geotechnique，1977，27（1）：53－74.

[14]DESRUES J，VIGGIANI G.Strain localization in sand：an overview of the experimental results obtained in Grenoble using stereophotogrammetry[J].International Journal for Numerical and Analytical Methods in Geomechanics，2004，28：279－321.

[15]SULEM J.Bifurcation theory and localization phenomena[J].European Journal of Environmental and Civil Engineering，2010，14（8－9）：989－1009.

[16]ABEYARATNE R，BHATTACHARYA K，KNOWELES J K.Stress－work functions with multiple local minima：modeling phase transformation using finite thermo－elasticity[M].∥ FU Y B，OGDEN R W.Non－linear elasticity：theory and applications.Cambridge，UK：Cambridge University Press，2001，431－490.

[17]FU Y B，ZHANG Y T.Continuum－mechanical modeling of kink－band formation in fibre－reinforced composites[J].International Journal of Solids and Structures，2006（43）：3306－3323.