Rayleigh面波作用下盆地場地響應特性研究

陳學良，高孟潭，李鐵飛

（中國地震局 地球物理研究所 工程地震學與城市減災研究室，北京100081）

盆地結構對地震動有顯著的放大效應。在國外，非常典型的是1985年墨西哥Ms 8.1級地震，遠在400多公里以外處于湖相沉積盆地之中的墨西哥城遭受了嚴重破壞，地震波在墨西哥城的湖相沉積盆地內多次反射，使得加速度放大、持續時間延長達到180秒左右，加速度峰值達0.18g[1]。而且，早在1957年距離震中170多公里的墨西哥城就發生了類似的破壞現象[2]。

地震Rayleigh面波被廣泛用于推斷不同尺度的結構特性（Lu，Maupin，et al.2008）[3]。從全球地震（Yoshizawa ＆Kennett 2004）[4]、巖土工程（Gucunski ＆ Woods 1992）[5]到超聲波無損檢測（NDT）（Mah ＆ Schmitt 2003）[6]等領域。通常實踐中最常見的工作，是從觀測數據（強震記錄、地震記錄或振（震）動數據）中提取Rayleigh面波相速度和群速度的頻散曲線，來反演地下結構特性、地形結構特性。但是，以純粹的Rayleigh面波地震動場作為輸入，考慮盆地沉積物特性對Rayleigh面波傳播特性的影響研究并不多見。最近，表面波從業人員的調查（O’Neill 2005）結果表明[7]，他們中的25%認為，沒有考慮到介質的非均質性是當前在巖土工程尺度上面波分析方法的主要問題。當大的變化（在實踐中常表現為地下局部異質體）發生時，波場變得很復雜，由二維或三維非均質性引起的散射波不容忽視（Herman et al，2000；Campman et al.2004）[8，9]。同樣，類似的現象也在超聲波實驗中得以看到（Nishizawa et al.1997；Scales ＆ Wijk 1999；Wijk et al.2004）[10－12]。正是基于這方面的考慮，開展了本項研究工作。

對于Rayleigh面波散射問題的求解，通常有unsturb方法（非擾動方法、試驗法），Born近似方法，WKBJ近似方法，Exact精確解方法。現在流行的一種方法－模態耦合方法，則是基于精確解方法。Snieder（1986a，b）基于遠場和Born近似，給出了三維結構中面波散射傳播的分析基礎—模態耦合方法。該方法展示了不同結構模式中散射波如何相互作用，方法適合于處理弱散射或弱異質性問題[13－14]。對于高頻和更強的異質性，Friederich et al.（1993）提出了多種前向散射設計，用來模擬3D各向同性結構的面波散射[15]。Maupin（2001）開發了多重散射程序來處理在任意各向同性和各向異性三維結構的面波傳播問題[16]。Cakir（2006）作了進一步發展以減少計算時間[17]。Lu，Maupin，et al.（2008）通過求解屈服面指向全波場而不需要迭代的積分方程，結合Maupin（2001）的方法，計算出了多重面波的散射[3]。

Born方法屬于考慮一階散射，WKBJ屬于二階近似，模態耦合方法本質上為解析方法，可以給出散射源體對每一個模態的解析影響，但計算復雜，計算效率相對低些。考慮到有限元方法剖分模型的靈活性（對于處理尖角、拐角等問題）、波動方法的波動傳播特性、波動有限元方法的計算高效性等特性，不再基于Exact方法—分模態研究最后疊加得到總散射波場的研究思路，而是通過波動有限元方法，研究Rayleigh面波地震動作用下盆地場地的地震動反應（理論地震圖）及其規律，直接得到體系已經考慮了各模態間多重相互作用的總散射波場。

周正華，溫瑞智等（2006）的Rayleigh波入射情形下的斷層效應[18]，劉晶波（1989）復雜地形對面波地震動的影響等工作[19]，對本項研究有很重要的啟示和借鑒作用。上述工作均采用了一階精度的中心差分格式，這里則采用了精度更高的Newmark“新”顯式數值積分格式（陳學良等，2011）[20]，這也是該項工作的一點特點。

1 波動有限元與Rayleigh面波輸入

廖振鵬及其合作者（廖振鵬等，1984；廖振鵬，1996a，1996b，2002）提出了解耦的近場波動數值模擬思想，即將多次透射公式（Multi－Transmitting，Formula，簡記為 MTF）與集中質量顯式有限元相結合[21－24]，常稱之為“波動有限元方法”。該方法的“內點”計算需要一種時域顯式數值積分格式，如前述，采用文獻[20]提出的Newmark“新”顯式數值積的第三種積分格式）。該方法在空間上是解耦的，在時間上是顯式的，相對于其它方法計算效率高，占用計算機內存小，極大地提高了有限元的求解能力。

以均勻彈性半空間Rayleigh面波的解析解作為地震動輸入。水平和豎向位移表達式分別為：

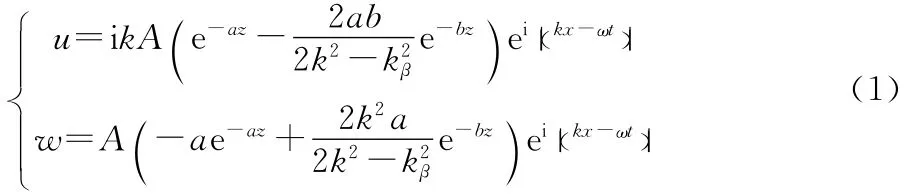
式中，k，a，b是介質剪切波速和泊松比的函數，i為虛數。為獲得輸入波形，設剪切波速為300m／s，泊松比為0.30，可求得Rayleigh波波速cR＝278.224m／s。設Ae－iωt為近似δ脈沖波，其函數解析表達式為：

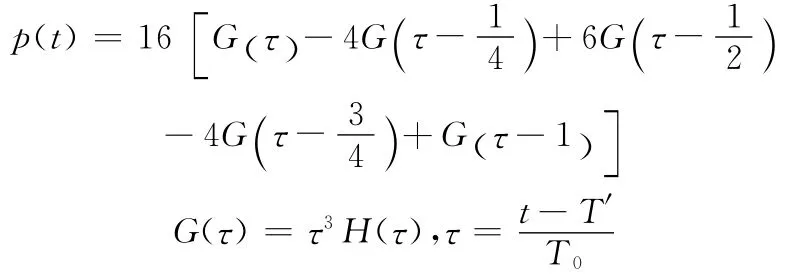
其中，取T0＝1s，T′＝3s，計算時間為10.24s，Δt＝0.005s，計算離散點數，則可得到水平位移u0（t）及豎向位移w0（t），等比例調整兩者幅值，使w0（t）的幅值為1.0，將此時u0（t）和w0（t）作為Rayleigh面波位移場的地表位移，相應放大了的Rayleigh面波位移場、速度場、加速度場作為盆地模型的地震動輸入。

2 盆地計算模型及其參數

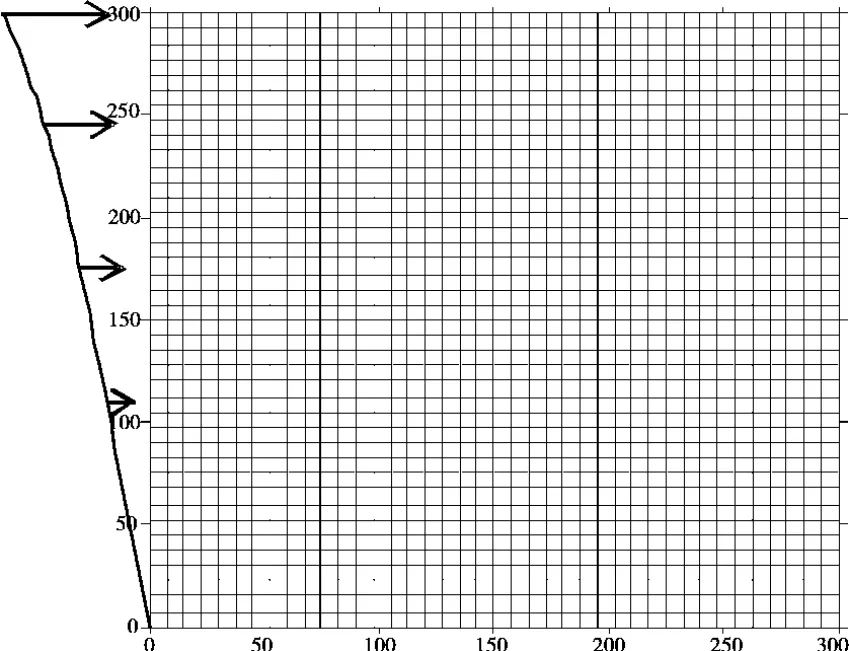
圖1 波動有限元盆地計算模型及入射波示意圖

圖1波動有限元盆地計算模型中，中間的方形陰影部分為盆地介質，左右兩側和底部的陰影區（U型區）為人工邊界區。中間的豎向粗線表示后面計算中將輸出這一列節點反應。最外側的節點為人工邊界節點，采用MTF三點二階（兩次）透射公式來計算人工邊界節點的反應。通過設置人工邊界，有效模擬半無限域。應用MTF時需進行波場分離，對于左側人工邊界區，散射波場為波動有限元計算的總波場（顯式波動有限元計算得到）減去入射波場（解析自由場）得到。對于右側人工邊界區和底邊界人工邊界區，散射場仍為總波場減去自由波場（解析解），但是，要注意考慮Rayleigh面波解析解的傳播時間延遲（有理論值）。

波動有限元方法計算體系反應時，要滿足時空離散和穩定性條件。采用在MTF算子中加上小的修正算子γB00的簡便處理方法（周正華、廖振鵬，2001）處理低頻漂移失穩問題[25]，γ＝0.004。阻尼比ξ＝0。

計算區域為300m×300m，有限單元網格尺寸為7.5m×7.5m，盆地尺寸為150m×150m，位置如圖1所示。周圍區域介質（非沉積盆地區域但包括邊界區）參數為：橫波波速β＝300m／s、密度ρ＝2 100kg／m3、泊松比ν＝0.30，阻尼比為零。當沉積盆地介質與周圍區域介質參數相同時，則計算區域僅為單一介質，理論上，Rayleigh面波將無波型轉換、無頻散、無衰減。因此，對該種情形進行了顯式波動有限元計算，并將計算結果與解析解（即自由場、入射場）進行了比較，效果良好（圖略）。該實例說明了計算程序的合理性和可靠性。

3 軟、硬盆地介質對地震動的影響

通過顯式波動有限元方法進行數值計算，分析當盆地介質由軟變硬時，盆地介質對Rayleigh面波地震動的影響規律。五種沉積盆地介質參數如表1所示。圖2、圖3中給出了情形1和情形4中間一列節點的Rayleigh面波地震動響應波形（其它圖略）。

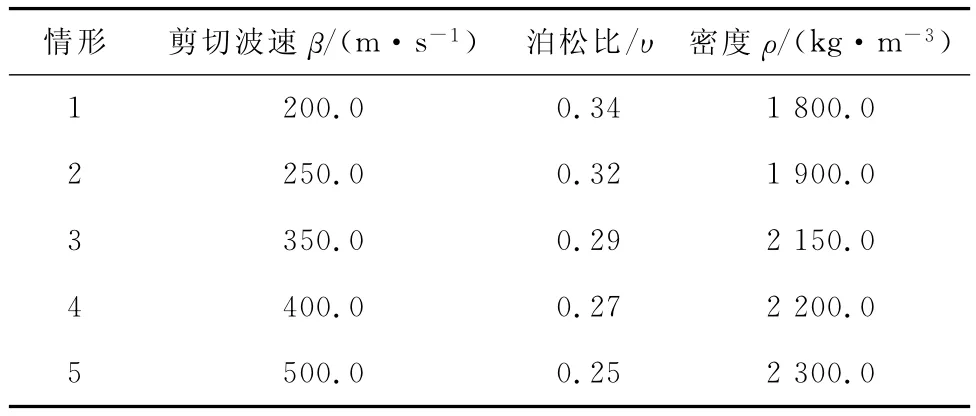
表1 沉積盆地介質參數

1）隨著沉積盆地介質由軟變硬，沉積盆地對Rayleigh面波地表地震動的放大作用，由大變小。

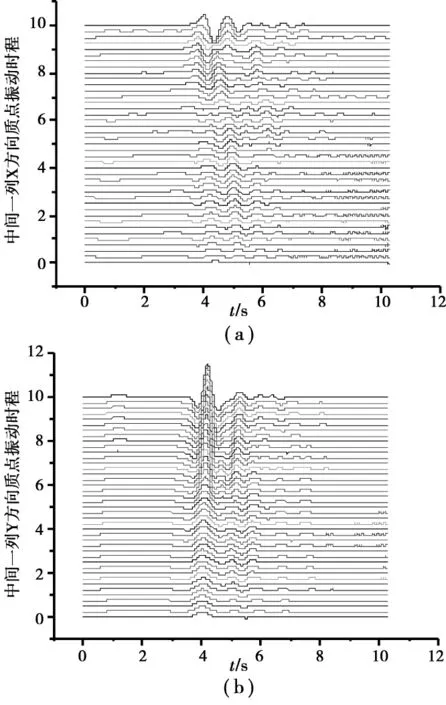
圖2 情形1模型所得到的Rayleigh面波響應

對于豎向Y 方向，5種情形分別為：1.536 32，1.259 68，0.874 10，0.758 71，0.607 66。而單一介質反應結果的最大值，水平X方向為－0.496 16，豎向Y 方向為1.000 00。介于情形2和情形3之間。

2）盡管有軟或硬的沉積盆地介質存在，但水平X方向和豎向Y方向最大響應區的地震動主波形，與Rayleigh面波地震動入射場相一致，未受到異常嚴重的改變。

3）從次波形來看，沉積盆地產生散射波的強度，同盆地介質與周圍介質之間波阻抗α的關系顯著，幾乎與成正比，而且水平X方向比豎向Y方向更明顯。情形1和情形5相比，軟盆地介質情形1產生的散射波更強烈。

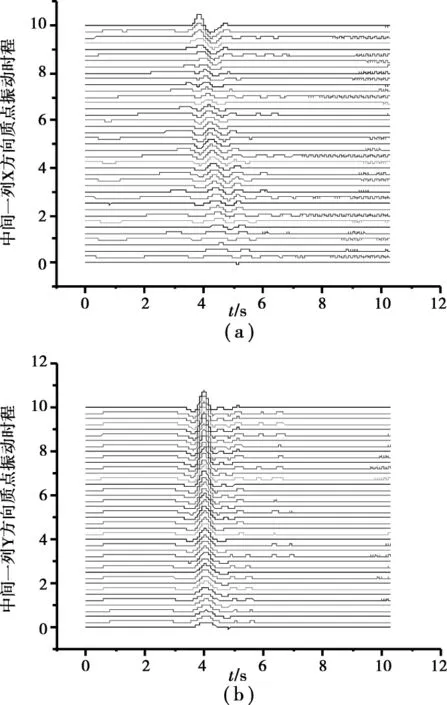
圖3 情形4模型所得到的Rayleigh面波響應

上述這些規律和特點，符合人們對Rayleigh面波傳播和散射特性的認識和理解[26]。

4 盆地尺寸對面波地震動的影響

分析沉積盆地的深度和寬度，對Rayleigh面波地震動的影響。分兩種工況：1.保持盆地的寬度150m不變，深度從原來150m增加到225m；2.保持盆地的深度不變150m，以中線對稱，寬度從原來150m減小至75m。限于篇幅，只給出工況2在介質參數情形2和情形4的相應反應圖形（如圖4，5）。通過比較分析，規律如下。

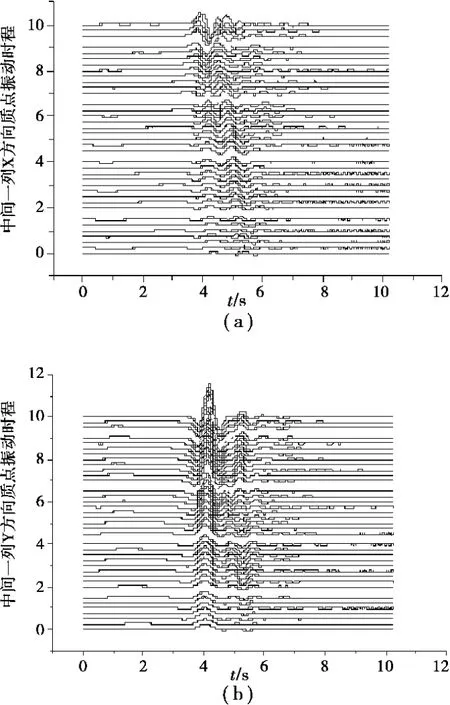
圖4 工況2在情形1（β＝200）的Rayleigh面波響應對比

圖5 工況2在情形4（β＝400）的Rayleigh面波響應對比

情形1中，盆地介質β＝200m／s時，75×150盆地與150×150盆地的Rayleigh面波響應相比，在水平X方向的振動到時要提前一些（早動），在豎向Y方向，振動到時基本相同，但振動波形要小（盆地介質的散射程度小些）。情形4盆地介質β＝400m／s時，相應結論恰與此相反。

情形1中，盆地介質β＝200m／s時，150×225盆地與150×150盆地相比，對于水平X方向的Rayleigh面波地震動反應，振動到時基本相同，而在豎向150m～225m的盆地區域，振動反應大，差別明顯。在豎向Y方向，振動到時滯后，在豎向150m～225m的盆地區域，振動反應也比較大。對于情形4盆地介質β＝400m／s時，相應結論基本與此相反。

這些結果和規律，體現了Rayleigh面波在軟介質中傳播時的放大效應和傳播慢的特點，與硬介質中的傳播規律相反[26]。

5 盆地模型的Rayleigh面波地震圖

圖6、圖7分別給出了150×150盆地場地模型，在盆地介質為情形1（β＝200m／s）時，Rayleigh面波在X方向和在Y方向的地震動傳播過程。先后各給出15幅傳播快照。其他情形（如情形4）的Rayleigh面波地震動傳播快照圖，請參閱文獻[26]。

圖5、圖6及相關圖形[26]給出的Rayleigh面波地震動的數值模擬結果一場地面波地震圖，較好地再現了Rayleigh面波在軟、硬方形盆地模型中從場地左側，經過盆地區傳播到場地右側的波導過程。從左側（x＝0，z＝0，y任意）、右側（x＝300m，z＝0，y任意）、底部（y＝0，z＝0，x任意）的人工邊界節點的Rayleigh面波地震動反應來看，不論是水平X方向還是豎向Y方向，均表現為自由透射，體現了MTF人工邊界的良好效果。

圖6 150×150盆地場地模型在盆地介質為情形1（β＝200m／s）時，Rayleigh面波在X方向的地震動傳播過程（15幅傳播快照）

同時，可以看出，軟、硬方形盆地的“邊緣效應”是明顯的，體現為在盆地邊緣節點的地震動反應不同于周圍介質，格外突出，即反應更大或者更小。軟、硬方形盆地中心區的“盆地放大效應”也是顯著的，軟、硬方形盆地介質不僅影響面波地震動的幅值（相對于單一介質而言），還影響面波地震動的持續時間。不管是水平X方向還是豎向Y方向，均可發現從盆地右側反射到盆地左側，然后再反射回的面波地震動波形。

6 結 論

計算分析了軟、硬盆地介質參數、盆地區域尺寸對Rayleigh面波地震動的影響規律，同時給出了盆地場地模型的Rayleigh面波地震圖及其傳播過程。這些結果和規律，有益于Rayleigh面波地震動在方形盆地區域場地模型中反射、透射及盆地角點激發的波型轉換等波動傳播規律的認識和理解。

分析中沒有涉及左、右邊界區域為多層介質的復雜場地模型，原則上講，只要提供左、右兩側成層介質的Rayleigh面波地震動入射場，波動有限元方法都可以計算分析。

圖7 150×150盆地場地模型在盆地介質為情形1（β＝200m／s）時，Rayleigh面波在Y方向的地震動傳播過程（15幅傳播快照）

[1]WILLIAM B.JOYNER.Strong motion from surface waves in deep sdimentary basins[J].Bulletin of the Seismological Society of America，2000，90（6B）：S95－S112.

[2]MARTIN C.DUKE A D，LEEDS J.Soil conditions and damage in the Mexico earthquake of July 28，1957[J].Bull.Seism.Soc.Am，1959，49（2）：179－191.

[3]LU LAIYU，VALERIE MAUPIN，ZENG RONGSHENG，et al.Scattering of surface waves modelled by the integral equation method[J].Geophys.J.Int.，2008：1－16.

[4]YOSHIZAWA K，KENNETT B.Multi－mode surface wave tomography for the australian region using a three－stage approach incorporating finite frequency effects[J].J.geophys.Res.，2004，109：B02310.

[5]GUCUNSKI N，WOODS，R.Numerical simulation of the SASW test[J].Soil Dyn.Earthq.Eng.，1992（11）：213－227.

[6]MAH M，SCHMITT D.Determination of the complete elastic stiffnesses from ultrasonic phase velocity measurements[J].J.geophys.Res.，2003，108（B1）：2016.

[7]O’NEILL，A.Seismic surface waves special issue：Guest editorial[J].J.Environ.Eng.Geophys.，2005，10（2）：67－85.

[8]HERMAN G，MILLIGAN P，HUGGINS R，et al.Imaging shallow objects and heterogeneities with scattered guided waves[J].Geophysics，2000，65：247－252.

[9]CAMPMAN X，WIJK，K V，RIYANTI C，et al.Imaging scattered seismic surface waves[J].Near Surface Geophys.，2004（2）：223－230.

[10]NISHIZAWA O，SATOH T，LEI X，et al.Laboratory studies of seismic wave propagation in inhomogeneous media using a laser doppler vibrometer[J].Bull.seism.Soc.Am.，1997，87：809－823.

[11]SCALES J A，WIJK K V.Multiple scattering attenuation and anisotropy of ultrasonic surface waves[J].Appl.Phys.Lett.，1999，74（25）：3899－3901.

[12]WIJK K，LEVSHIN.Surface wave dispersion from small vertical scatters[J].Geophys.Res.Lett.，2004，31：L20602.

[13]SNIEDER R.3－d linearized scattering of surface waves and a formalism for surface wave holography[J].Geophys.J.R.astr.Soc.，1996a，84：581－605.

[14]SNIEDER R.The influence of topography on the propagation and scattering of surface waves[J].Phys.Earth planet.Inter.，1986b，44：226－241.

[15]FRIEDERICH W， WIELANDT， STANGE S. Multiple forward scattering of surface waves：comparison with an exact solution and Born single scattering methods[J].Geophys.J.Int.，1993，112：264－275.

[16]MAUPIN V. A multiple－scattering scheme for modelling surface wave propagation in isotropic and anisotropic threedimensional structures[J].Geophys.J.Int.，2001，146：332－348.

[17]CAKIR O.The multilevel fast multipole method for forward modeling the multiply scattered seismic surface waves[J].Geophys.J.Int.，2006，167（2）：663－678.

[18]周正華，溫瑞智，毛國濱，等.Rayleigh波入射情形下的斷層效應[J].地震工程與工程振動，2006，26（5）：1－6.

[19]劉晶波.波動的有限元模擬及其復雜場地對地震動的影響[D].哈爾濱：國家地震局工程力學研究所，1989.

[20]CHEN XUE－LIANG，GAO MENG－TAN，TAO XIA－XIN.Newmark “New”Explicit Step－by－step Integration Formulas[J].Journal of Harbin Institute of Technology（New Series），2009，16（Sup.1）：84－91.

[21]LIAO ZHENG－PENG，WONG HL.A transmitting boundary for the numerical simulation of elastic wave propagation[J].Soil Dynamics and Earthquake Engineering，1984，3（4）：174－183.

[22]LIAO ZHENG－PENG.Extrapolation nonreflecting boundary conditions[J].Wave Motion，1996a，24：117－138.

[23]廖振鵬.工程波動理論導引（第一版）[M].北京：科學出版社，1996b.

[24]廖振鵬.工程波動理論導引（第二版）[M].北京：科學出版社，2002.

[25]周正華，廖振鵬.消除多次透射公式漂移失穩的措施[J].力學學報，2001，33（4）：550－553.

[26]陳學良.復雜場地地震反應的若干問題研究[R].北京：中國地震局地球物理研究所，2009.