堆石蠕變與顆粒破碎特性三軸試驗

王 琛，詹傳妮，何 鵬，張建衛，李 黎

(四川大學a.水力學與山區河流開發保護重點實驗室；b.水利水電學院，成都610065)

顆粒材料的流變性質研究是巖土力學與工程的重要課題[1－4]。如對高面板堆石壩，堆石顆粒材料的流變將引起面板和墊層分離，導致面板壓應力增大而壓裂，危害壩體防滲和安全[5－6]。

顆粒材料流變性質研究包括蠕變、應力松弛和應變速率效應[2－3]，迄今，堆石的流變性質研究主要集中在蠕變規律和機理研究方面[7－10]。堆石的蠕變規律宜通過大型三軸試驗獲取[7]，蠕變與時間關系有冪函數[8－9]和雙曲線函 數[10]等，且與應力水平有關。花俊杰等[9]對堆石蠕變的尺寸效應進行了試驗分析。一般認為結合細觀機理去分析材料的宏觀力學行為是建立更加合理本構的可行途徑。從細觀機理來看，堆石體在應力持續作用下顆粒破碎，細化破碎的顆粒結構調整、滑移填充孔隙，這在宏觀上表現為蠕變現象[11]。初步的堆石顆粒破碎研究分析了顆粒破碎與應力的關系[11]。然而，在顆粒破碎指標的合理選取，及其與應力、蠕變等的定量關系等方面尚有不足。

本文采用分別加載方式，對兩河口堆石料進行了不同圍壓，不同應力水平下的大型三軸排水蠕變試驗，獲取堆石蠕變規律；并用篩分法測量試驗后堆石顆粒級配，初步探討蠕變與顆粒破碎的關系。

1 三軸排水蠕變試驗

1.1 試驗程序

三軸排水蠕變試驗在應力控制式大型三軸儀上開展。試驗土料采用兩河口板巖堆石料，試樣尺寸φ300×600mm，對粒徑d＞60mm超徑土以5～60 mm等量替代法處理，其不均勻系數Cu＝4.2，曲率系數Cc＝0.81，分類定名為級配不良礫GP。試樣控制干密度1.95g／cm3，分5層制樣以保證試樣的均勻性。采用真空和水頭法聯合飽和，試驗水溫20±2℃。

試驗考慮了圍壓σ3和偏應力q＝σ1－σ3的影響，σ1為大主應力。試驗分2組，編號為TC2和TC4，對應σ3＝200kPa和400kPa。每組各進行4個偏應力下的蠕變試驗，以應力水平表示偏應力的相對大小，qf為相應σ3下的破壞偏應力，由固結排水三軸試驗獲得；設置D＝0.25、0.50、0.75和0.95。試驗編號及其對應的應力狀態見表1，其中為平均法向應力。

為測量不同σ3和q情況下堆石的顆粒破碎，蠕變試驗采用分別加載方式進行。各試樣蠕變試驗程序如下：1)在給定σ3下固結24h。2)以較快的加載速率在2min內加載至預定的偏應力q。3)保持荷載穩定，測定隨時間t變化的軸向變形和體積變形，并根據面積校正微調荷載，保證加載應力恒定。4)加載2 880min后結束試驗，并進行顆粒篩分以獲取試驗后顆粒級配。

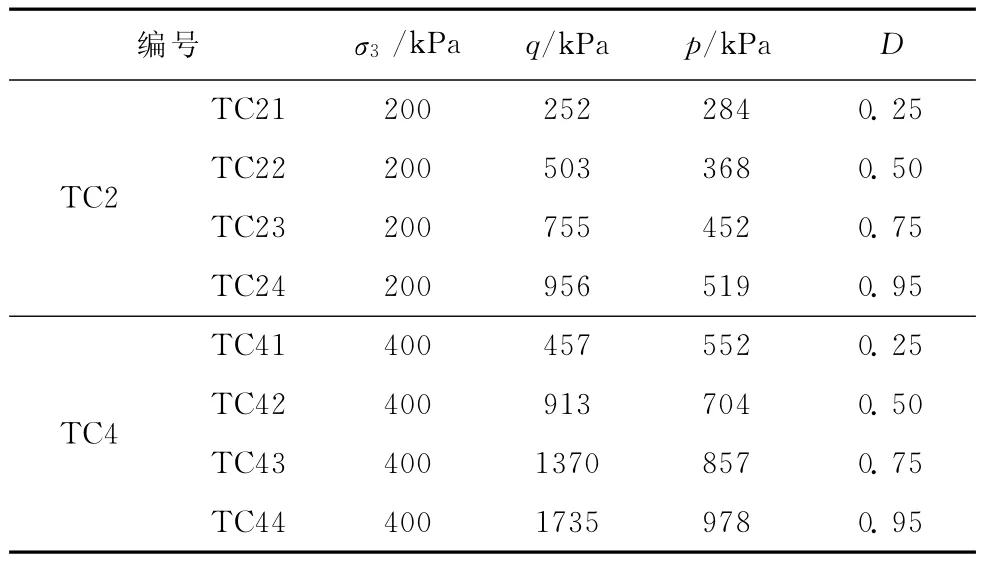
表1 試驗編號與應力狀態

1.2 試驗結果及其分析

對于堆石蠕變，蠕變變形起始時間是一重要問題。于浩等對堆石料選取1h作為劃分主壓縮變形和蠕變變形的時刻[9]，但缺乏理論依據。對固結排水試驗的剪切速率，吉甫遜建議破壞歷時tf[12]為

式中：h為排水距離，本次試驗為30cm；Cv為消散系數；η為系數，兩端排水時可取3.0；Uf為試樣的平均消散度。若取Uf＝0.99，Cv＝3 000cm2／s，得tf＝10s。鑒于此，并基于試驗測試精度，定義由加載初始至應力保持恒定后1min內產生的變形為相對瞬時變形，其后產生的變形為蠕變變形，則軸向應變和體積應變的總應變由相對瞬時應變和蠕應變組成。σ3＝200kPa和400kPa下的軸向應變εa～t關系和體積應變εv～t關系如圖1和圖2所示；表2列出了總軸向應變和總體積應變及其瞬時分量和蠕變分量。可知：

1)堆石顆粒材料發生了較明顯的隨時間增長的變形，即蠕變。其產生原因有以下2點：(1)隨著荷載施加直至穩定，顆粒接觸點所受的剪力和法向應力發生變化，則顆粒位置重新調整；該調整引起顆粒接觸面積的改變，則顆粒接觸點所受應力隨之發生變化；該細觀應力和變形的反復循環調整，為一個隨時間發展的過程，宏觀表現為堆石蠕變現象，即發生隨時間變化的變形[13]。(2)堆石顆粒受力后發生顆粒破碎，其破碎來源于較大的接觸應力導致的顆粒棱角破碎，以及顆粒內部裂紋的發生發展以致顆粒的整體破碎。顆粒破碎后的相對位移、相互充填和結構調整宏觀上即表現為蠕變[11]。

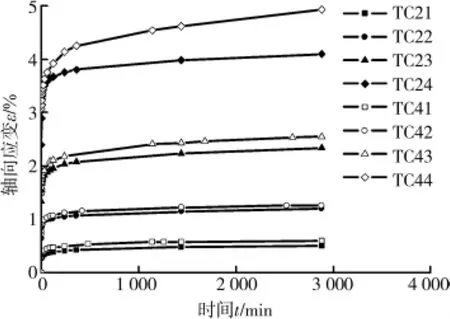
圖1 軸向應變εa－時間t關系曲線

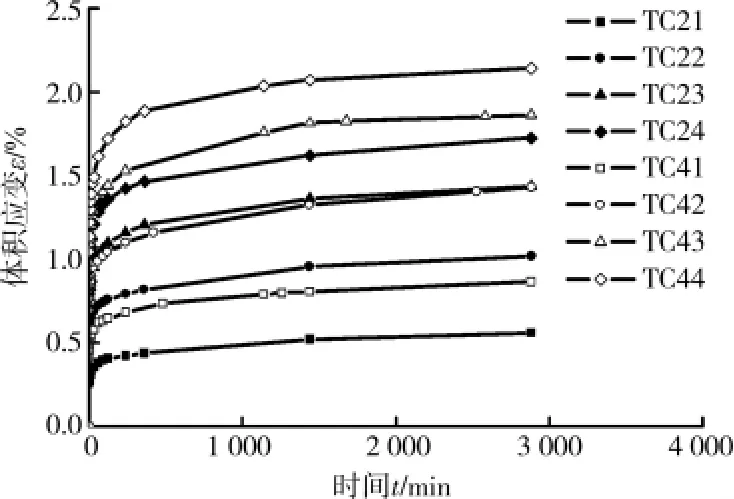
圖2 體積應變εv－時間t關系曲線

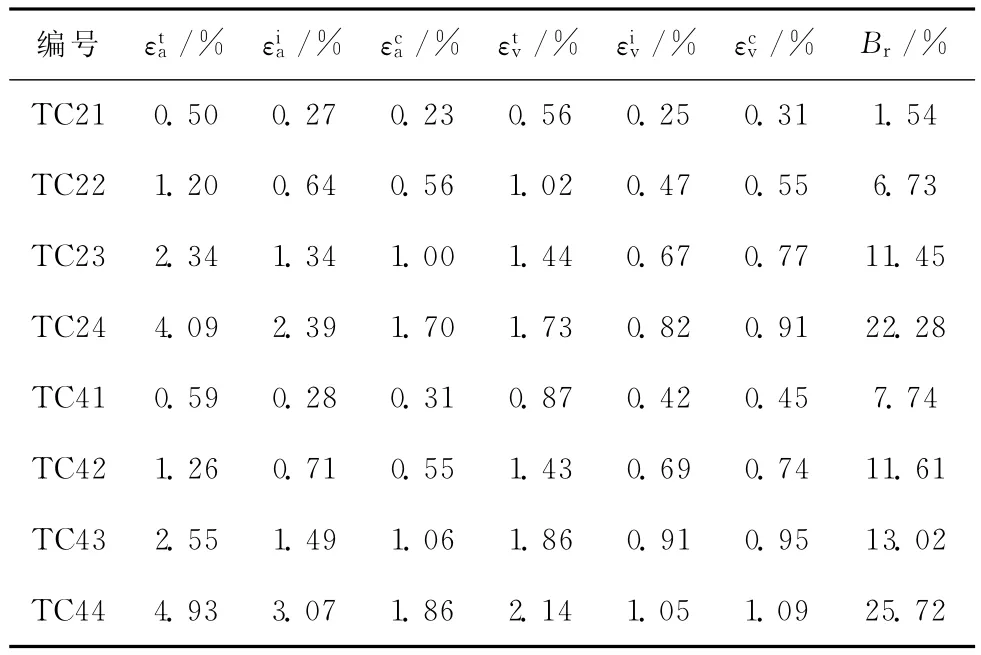
表2 三軸蠕變試驗結果

2)蠕應變曲線分衰減蠕變和勻速蠕變階段。衰減蠕變階段蠕應變增長較快，但增長速率逐漸衰減，且衰減速率較快，一般在240min后進入勻速蠕變階段，該階段蠕應變增量較小，且應力水平較小時迅速趨于穩定值。然而，面板堆石壩堆石體變形完成所需時間較長，故室內試驗結果應結合實際工程變形資料反饋分析后參考取用。

3)隨應力水平D的提高，總應變、相對瞬時應變和蠕應變皆增大。D一定時隨圍壓σ3增大，顆粒破碎增多，蠕應變相應增大。

2 蠕變規律

2.1 應變－時間方程

總應變ε一般可寫成如下形式[14]：式中，εr為參考應變；G(t)為時間t的函數。

時間函數G(t)表示應變－時間關系，可以選用不同的函數形式，包括冪函數、對數函數和雙曲線函數等。數據分析表明堆石蠕變與時間的關系以冪函數擬合較好，式(2)可寫成，

式中：tr為參考時間，對于試驗結果分析，可取tr＝1min；n為關系曲線的斜率，圖3給出了σ3＝200kPa時的關系曲線。各參數見表3，其中，εar和εvr分別表示軸向和體積參考應變，na和nv分別表示軸向和體積斜率。

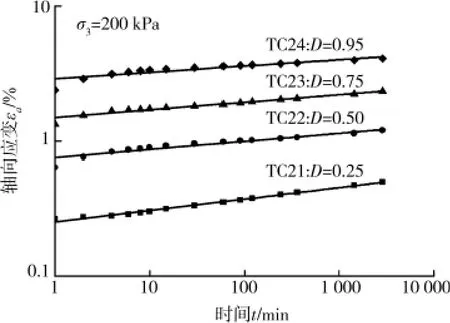
圖3 關系曲線

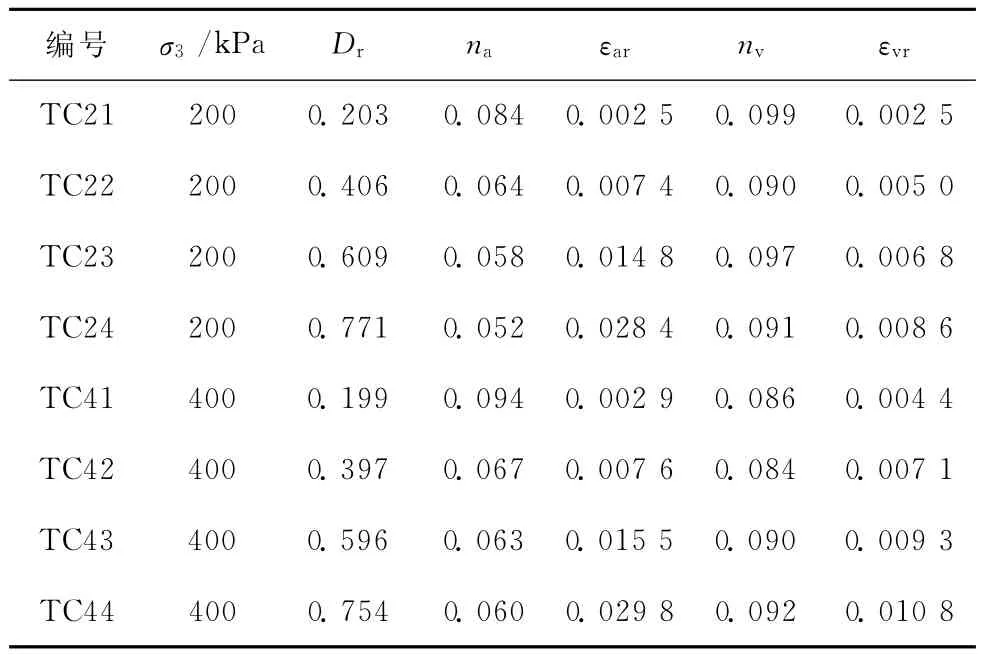
表3 應變－時間關系參數

2.2 應力－應變方程

εar表示軸向應變－應力關系，一般為應力水平的雙曲線函數和指數函數等，本文采用雙曲線函數擬合，即

經坐標變換有

式中，ar和br為模型參數，分別為關系曲線的截距和斜率；Dr為t＝tr時應力－應變關系的應力水平，與前文中的D稍有差別。σ3＝200kPa時的關系曲線如圖4所示，參數取值見表4。

εvr表示體積應變－應力關系，本文假定其與Dr成線性比例關系，即

式中：cr為方程參數，為εvr－Dr關系曲線的斜率，計算值見表4。

2.3 應力－應變－時間方程

對于軸向應變，分析表明以冪函數和雙曲線函數擬合應變－時間關系和應力－應變關系較好。將式(4)代入式(3)，得 Mesri應力水平－軸向應變－時間方程[14]：

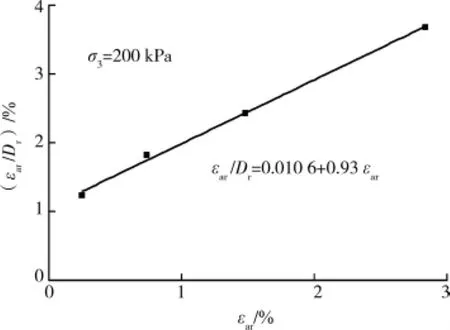
圖4 關系曲線

表4 應力－應變關系參數

對于體積應變，分析表明以冪函數和線性函數擬合應變－時間關系和應力－應變關系較好。將式(6)代入式(3)，得應力－體積應變－時間方程，

3 蠕變與顆粒破碎關系

3.1 相對顆粒破碎指數

顆粒破碎的合理度量是進行顆粒材料破碎研究的重要前提。目前度量顆粒破碎的參數主要有[15]：1)以某一特征粒徑的變化來衡量顆粒破碎的程度，如特征粒徑d15。2)試驗前后粒組含量變化絕對值之和，如 Marsal的破碎率Bg。3)比表面積增量。4)體積破碎率指標[16]。5)級配面積表示的相對破碎指數[17]，該參數因直觀方便且概念清晰從而得到了廣泛應用[15，18]。

Hardin[17]認為顆粒材料將最終破碎于某一界限粒徑，并取界限粒徑dm＝0.074mm。定義試驗前后級配曲線與dm＝0.074mm豎線所圍的面積分別為初始破碎勢Bpi和Bpf，破碎量Bt＝Bpi－Bpf，則可定義相對顆粒破碎指數，即為某一狀態下顆粒破碎量與初始破碎勢的比值。然而，顆粒破碎的最終形式將是顆粒分布趨于一自相似的質量分形結構[19－20]，即最終

級配曲線Fu可表示為

式中：d和dM分別為粒徑和最大粒徑；α為分形維數。顆粒材料經破碎后的最終級配的分形維數為2.5～2.6，本文取α＝2.5。

基于自相似分形結構的最終顆粒級配，Einav[21－22]修正 Hardin的相對顆粒破碎指數Br為

式中：Bt和Bp分別為某一狀態級配曲線和最終級配曲線與初始級配曲線所圍面積。考慮到堆石粒徑大，粒徑小于0.074mm的顆粒含量較少，其對破碎勢的貢獻較小，故修正Bt和Bp分別為某一狀態級配曲線和最終級配曲線與初始級配曲線及dm＝0.074mm豎線所圍面積，如圖5所示。故可定義相對顆粒破碎指數Br，見式(10)。

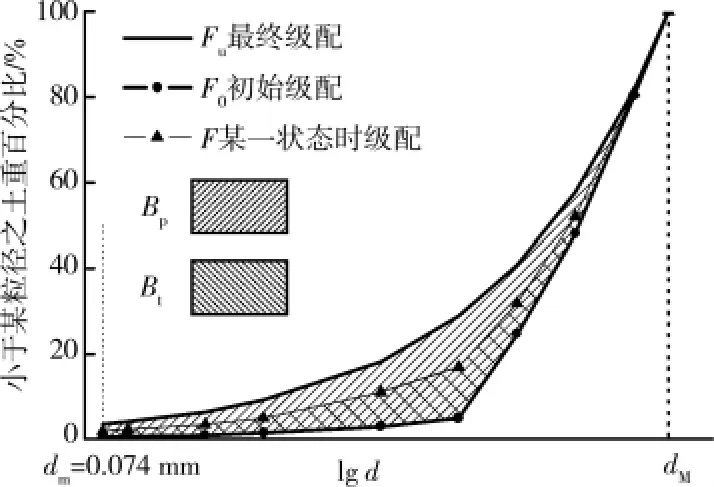
圖5 相對顆粒破碎指數示意圖

3.2 蠕變與相對顆粒破碎指數關系

堆石料的初始級配F0、經三軸排水蠕變試驗后的級配曲線和分形維數α＝2.5的Fu見圖6，圖中縱坐標以對數坐標表示，以便清晰表示各級配曲線。由式(10)計算出各圍壓和應力水平下的Br見表2。可知：相同圍壓條件下，應力水平增大，級配曲線漸由初始級配向最終級配移動，相對顆粒破碎指數增大，原因為平均法向應力和偏應力的增大引起顆粒破碎增多；應力水平相同時，圍壓增大，由于平均法向應力的增大，顆粒破碎亦增多。

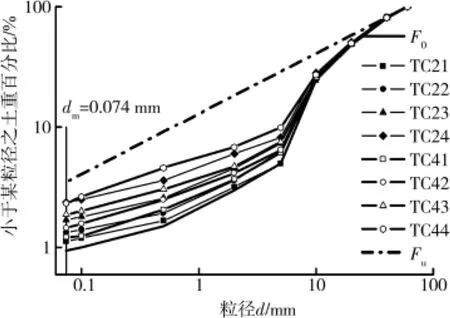
圖6 蠕變試驗后級配曲線

為分析堆石蠕變機理，獲得蠕變變形與顆粒破碎的關系，繪制軸向蠕變εca和體積蠕變εcv與相對顆粒破碎指數Br關系，見圖7。可見，除個別點外，該關系呈現良好的線性關系，表明堆石的蠕變變形，包括軸向蠕變和體積蠕變隨著顆粒的逐漸破碎逐漸增大，二者存在近似的線性比例關系，有

式中：αa、αv和βa、βv分別為關系曲線的截距和斜率。圖7給出了擬合曲線，其中，在擬合關系曲線時，對個別離異數據未采用。參數αa和αv表示相對顆粒破碎指數Br＝0時，由于堆石顆粒位置發生調整而引起的，分別為0.144%和0.343%。參數βa和βv表示顆粒破碎對的影響程度，值越大表示顆粒破碎引起的蠕應變越大。其值分別為0.069和0.030，可知顆粒破碎對軸向蠕應變的影響大于體積蠕應變。

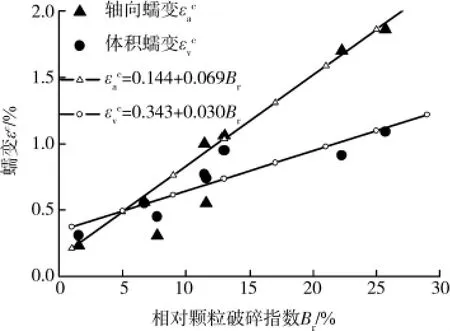
圖7 蠕變εc－相對顆粒破碎指數Br關系

4 結 語

采用分別加載方式，對兩河口堆石料進行了不同圍壓，不同應力水平下的大型三軸排水蠕變試驗，并在試驗后測量顆粒破碎情況，分析了堆石蠕變規律及其與顆粒破碎的關系，結論如下：

1)堆石受荷后將發生相對瞬時變形和較明顯的蠕變變形；給出了不同偏應力水平和圍壓下的總變形、相對瞬時變形和蠕變變形；軸向蠕變和體積蠕變隨應力水平的增大而增大，應力水平一定時隨圍壓的增大而增大。

2)堆石的應變－時間關系滿足冪函數，應力－軸向應變關系符合雙曲線函數，應力－體積應變關系符合線性比例關系。

3)隨應力水平和圍壓的增大，顆粒破碎增多。采用相對顆粒破碎指數分析了堆石經蠕變試驗后的顆粒破碎情況，表明軸向蠕變和體積蠕變皆近似與相對顆粒破碎指數呈線性比例關系。

[1]王者超，李術才.高應力下顆粒材料一維力學特性研究(Ⅱ)：蠕變性質[J].巖土力學，2010，31(11)：3392－3396.WANG ZHE－CHAO，LI SHU－CAI.One－dimensional mechanical behavior of granular materials at high stresses(PartⅡ)：Creep behavior[J].Rock and Soil Mechanics，2010，31(11)：3392－3396.

[2]LADE P V，LIGGIO C D JR，NAM J.Strain rate，creep and stress drop－creep experiments on crushed coral sand[J].Journal of Geotechnical and Geoenvironmental Engineering，2009，135(7)：941－953.

[3]LADE P V，NAM J，LIGGIO C D JR.Effects of particle crushing in stress drop－relaxation experiments on crushed coral sand[J].Journal of Geotechnical and Geoenvironmental Engineering， 2010， 136 (3)：500－509.

[4]WANG FEI，MIAO LIN－CHANG，LV WEI－HUA.Experimental study on the creep behavior of the Yangtze river sand[C]／／FRATTA D O，PUPPALA A J，MUHUNTHAN B.GeoFlorida 2010：Advances in Analysis，Modeling ＆Design(GSP 199)，February 20－24，2010，West Palm Beach，Florida.Reston，VA：Geo－Institute of ASCE，2010：777－782.

[5]花俊杰，常曉林，周偉.高堆石壩流變研究進展[J].水力發電學報，2010，29(4)：194－199.HUA JUN－JIE，CHANG XIAO－LIN，ZHOU WEI.Advances in researches on creep of high rock－fill dams[J].Journal of Hydroelectric Engineering，2010，29(4)：194－199.

[6]OLDECOP L A，ALONSO E E.Theoretical investigation of the time－dependent behaviour of rockfill[J].Geotechnique，2007，57(3)：289－301.

[7]左永振，程展林，丁紅順，等.堆石料蠕變試驗方法研究[J].長江科學院院報，2009，26(12)：63－65，70.ZUO YONG－ZHEN，CHENG ZHAN－LIN，DING HONG－SHUN，et al.Method research for rockfillcreep test[J].Journal of Yangtze River Scientific Research Institute，2009，26(12)：63－65，70.

[8]于浩，李海芳，溫彥鋒，等.九甸峽堆石料三軸蠕變試驗初探[J].巖土力學，2007，28(S)：103－106.YU HAO，LI HAI－FANG，WEN YAN－FENG，et al.Study on triaxial creep test for Jiudianxia rockfill materials[J].Rock and Soil Mechanics，2007，28(S)：103－106.

[9]花俊杰，周偉，常曉林，等.堆石體應力變形的尺寸效應研究[J].巖石力學與工程學報，2010，29(2)：328－335.HUA JUN－JIE，ZHOU WEI，CHANG XIAO－LIN，et al.Study of scale effect on stress and deformation of rockfill[J].Chinese Journal of Rock Mechanics and Engineering，2010，29(2)：328－335.

[10]王海俊，殷宗澤.堆石流變試驗及雙屈服面流變模型的研究[J].巖土工程學報，2008，30(7)：959－963.WANG HAI－JUN，YIN ZONG－ZE.Creep tests of rockfill and double－yield surface creep model[J].Chinese Journal of Geotechnical Engineering，2008，30(7)：959－963.

[11]梁軍，劉漢龍，高玉峰.堆石蠕變機理分析與顆粒破碎特性研究[J].巖土力學，2003，24(3)：479－483.LIANG JUN，LIU HAN－LONG，GAO YU－FENG.Creep mechanism and breakage behaviour of rockfill[J].Rock and Soil Mechanics，2003，24(3)：479－483.

[12]南京水利科學研究院.SL237－1999土工試驗規程[S].北京：中國水利水電出版社，1999.

[13]TATSUOKA F，BENEDETTO H D，ENOMOTO T，et al.Various viscosity types of geomaterials in shear and their mathematical expression[J].Soils and Foundations，2008，48(1)：41－60.

[14]LIN H D，WANG C C.Stress－strain－time function of clay[J].Journal of Geotechnical and Geoenvironmental Engineering，1998，124(4)：289－296.

[15]魏松，朱俊高，錢七虎，等.粗粒料顆粒破碎三軸試驗研究[J].巖土工程學報，2009，31(4)：533－538.WEI SONG，ZHU JUN－GAO，QIAN QI－HU，et al.Particle breakage of coarse－grained materials in triaxial tests[J].Chinese Journal of Geotechnical Engineering，2009，31(4)：533－538.

[16]孔德志，張其光，張丙印，等.人工堆石料的顆粒破碎率[J].清華大學學報：自然科學版，2009，49(6)：795－799.KONG DE－ZHI， ZHANG QI－GUANG， ZHANG BING－YIN，et al.Particle breakage ratio of artificial rockfill materials[J].Journal of Tsinghua University：Science and Technique Edition，2009，49(6)：795－799.

[17]HARDIN C S.Crushing of soil particles[J].Journal of Geotechnical Engineering，1985，111(10)：1177－1192.

[18]KARIMPOUR H，LADE P V.Time effects relate to crushing in sand[J].Journal of Geotechnical and Geoenvironmental Engineering， 2010， 136 (9)：1209－1219.

[19]TURCOTTE D L.Fractals and fragmentation[J].Journal of Geophysical Research，1986，91(B2)：1921－1926.

[20]BEN－NUN O，EINAV I.The role of self－organization during confined comminution of granular materials[J].Philosophical Transactions of the Royal Society A，2010，368：231－247.

[21]EINAV I.Breakage mechanics—PartⅠ：Theory[J].Journal of the Mechanics and Physics of Solids，2007，55：1274－1297.

[22]EINAV I.Breakage mechanics—Part Ⅱ：Modelling granular materials[J].Journal of the Mechanics and Physics of Solids，2007，55：1298－1320.