一種筒蓋系統載荷計算方法

方國強,楊 為,李曉暉

(1.海軍裝備部,北京 100841;2.中國船舶重工集團公司第七一三研究所,河南 鄭州 450015)

0 引 言

發射導彈時推動導彈運動的工質氣體中有氣體、液體和固體,其三相混合,相互作用。這些工質氣體是高溫高壓及高速運動的瞬態流,并在筒口區域形成1個復雜的筒口壓力場。該筒口壓力場是發射裝置筒蓋系統的主要外負荷,它關系著筒蓋的安全。在以往的計算中,筒蓋正反兩面共布置了8個壓力測點,然后求出筒蓋正反面的合力得出筒蓋的最大載荷并求出相應的力矩。這種方法的主要缺點是布置測點困難、處理數據和計算過程麻煩。本文在以往的研究基礎上,運用最小二乘法推導出了2個計算較為方便的經驗公式,即計算公式和預測公式。計算公式是指在試驗完成后根據實測的出筒壓力、導彈出筒速度、工質氣體溫度等數據推導出的筒蓋最大載荷及力矩經驗公式;預測公式是指在導彈發射前,通過預定的導彈出筒速度推導出的筒蓋最大載荷及力矩經驗公式。

1 筒口壓力場形成機理及筒蓋系統載荷分析

1.1 筒口壓力場形成機理

水下發射導彈時,當彈尾離開發射筒口的瞬間,具有一定壓力的發射工質氣體從筒口溢出,在水中形成燃氣泡,此燃氣泡內的能量就從氣泡表面以壓力波的形式輻射出去,因而在發射筒口附近形成一個壓力場。

由于初始時刻燃氣泡內的壓力值大大超過平衡流體的靜壓力值,因此在輻射壓力波的同時,燃氣泡將會迅速膨脹,緊靠燃氣泡的水就產生徑向位移,我們稱它為水的擴散流動。隨著擴散流動過程的發展,燃氣泡內的壓力逐漸減小。由于水的慣性作用,燃氣泡進一步膨脹,使得燃氣泡內的壓力繼續下降,此時氣泡內的壓力小于氣泡外界壓力,膨脹速率逐漸降低,到某一時刻,氣泡膨脹停止,此時由于氣泡內的壓力小于氣泡外海水的壓力,氣泡開始收縮,到某一時刻,氣泡內氣體的壓力又與外界壓力相等,由于水的慣性作用,使得氣泡繼續被壓縮,收縮速率逐漸降低,并且在某一時刻收縮速率為0,這樣便結束了氣泡的第1次脈動循環,接著又開始第2次循環……,通常把這個過程稱為氣泡的膨脹脈動或氣泡的脈動。當然,由于燃氣泡內能量損失,其壓力不可能達到初始值,其脈動的峰值也迅速下降。圖1為水下發射試驗時實測的筒口壓力場曲線。

圖1 筒口壓力場實測壓力曲線Fig.1 Muzzle pressure field curve in the test

1.2 筒口壓力場作用下筒蓋負荷分析

在導彈發射前,若不考慮海流和潛艇的運動,那么筒蓋周圍是靜水,其壓力由水深確定,此時,水介質對筒蓋的合力為0。導彈發射時,周圍的水被推開,筒蓋受到水流的作用,在朝向筒口的一面受到的力較大,背向筒口的一面受到的力較小。由于筒蓋2個面上受到不等負荷,使筒蓋產生了1個合力作用。這是導彈運動時對壓力場的貢獻。理論和試驗證明,導彈運動速度越大,筒蓋受到的合力越大。

在導彈尾部離開筒口瞬間,筒內的發射工質氣體噴出發射筒,在筒口形成的燃氣泡處于膨脹階段時,氣泡就推動筒口周圍的靜水向外流動;反之,當燃氣泡處于收縮階段時,在筒口周圍的水流場形成匯合流動,其水流方向是從遠處流向筒口內匯合。由于筒口燃氣泡的膨脹、收縮運動,便形成了筒口周圍的變化水流場,水流場的強弱與燃氣泡具備的能量有關。能量的大小取決于氣泡內的壓力與工質氣體的溫度,并與壓力和溫度成正比。

2 經驗公式推導

通過以上筒口壓力場的分析可以知道,影響筒口壓力場的主要因素有導彈出筒時筒內壓力P,導彈出筒速度V,工質氣體溫度T。其中出筒時筒內壓力P代表了筒口壓力場的勢能指標,出筒速度平方V2代表了筒口壓力場的動能指標,工質氣體溫度T代表了筒口壓力場的內能。

2.1 計算公式推導

理論分析筒口壓力場最大載荷F與最大載荷力矩W都與P,V2和T成線性關系,即:

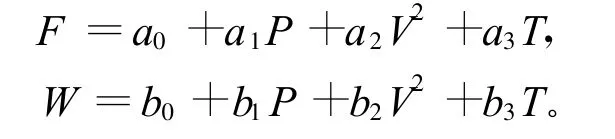
式中:F,W,P,V2,T為某型試驗的實測值;a0,a1,a2,a3,b0,b1,b2和b3為待定參數。

根據11發試驗的測試結果,利用最小二乘多元線性回歸方法來確定a0,a1,a2,a3,b0,b1,b2和b3這8個參數,以筒蓋所受最大載荷為例,最小二乘多元線性回歸方法如下:

取回歸方程

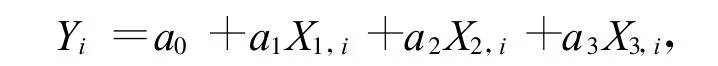
其中Yi,X1,i,X2,i,X3,i分別對應第i發彈實測的F,P,V2和T。將11發試驗實測數據代入回歸方程有:

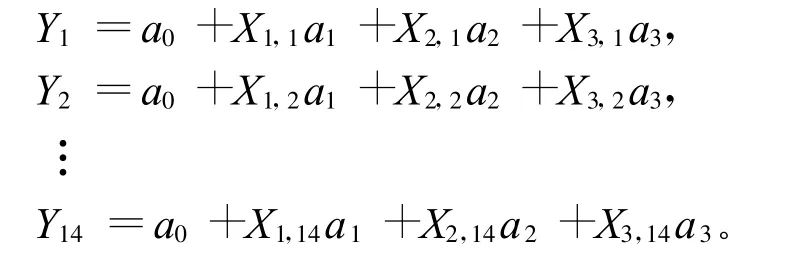
要選擇4個參數a0,a1,a2和a3同時滿足這11個方程是不可能的,為使這些方程盡可能滿足,令:

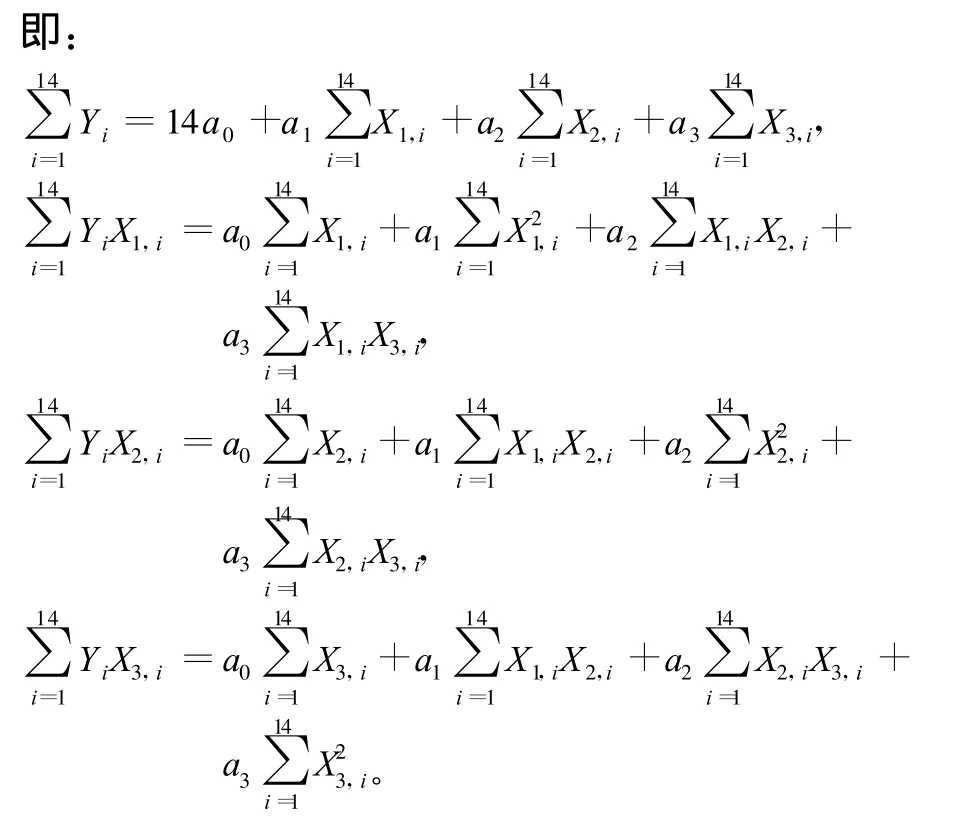
將數據代入以上4式并求解得:

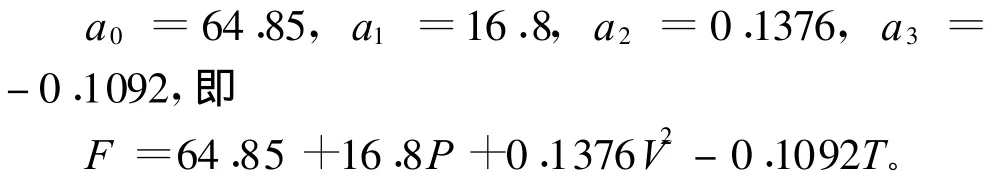
用同樣的方法可求得:

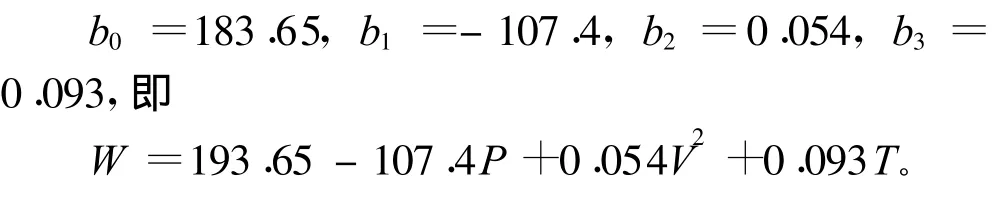
2.2 預測公式推導

由于導彈出筒時筒內壓力為不確定因素,波動范圍較大,所以在導彈發射前,導彈出筒時筒內壓力是未知的,同樣工質氣體溫度也是未知的。而在現實中往往需要在發射前就預測筒蓋所受到的最大載荷及最大載荷力矩,以預測筒蓋是否安全。所以根據2.1節中2個經驗公式是不能預測的,必須依靠其他已知條件來實現這一推測。

我們知道,在導彈發射前導彈的出筒速度是預定的,而且發射時發射動力系統能按要求進行發射能量調節,使出筒速度誤差范圍比較小。所以能根據預定出筒速度進行發射前導彈最大載荷及最大載荷力矩預測。

同樣運用最小二乘法進行推導,令:

利用第2.1節中的方法可得:

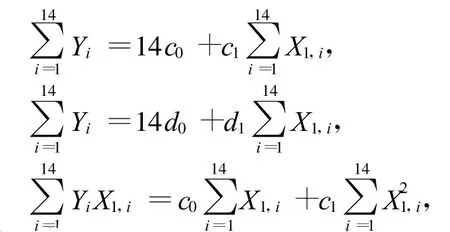
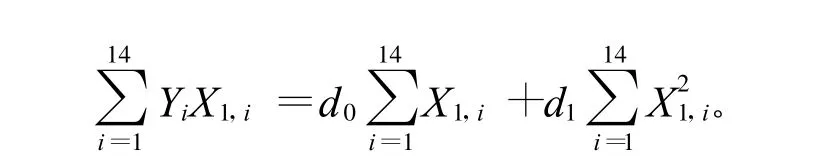
將數據代入得:

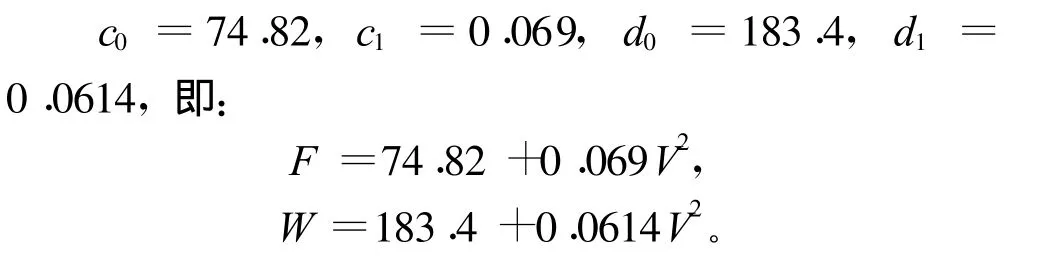
3 最大載荷及力矩值的比較

根據以上推導出的經驗公式,對各發次試驗的筒蓋最大載荷值及最大載荷力矩進行了計算,并與實測值進行了對比。表1為筒蓋最大載荷經驗公式計算結果與實測結果對比,表2為筒蓋最大載荷力矩經驗公式計算結果與實測結果對比。

表1 筒蓋最大載荷經驗公式計算結果與實測結果對比Tab.1 Comparison of themaximal load on the hatch of experience formula and test data

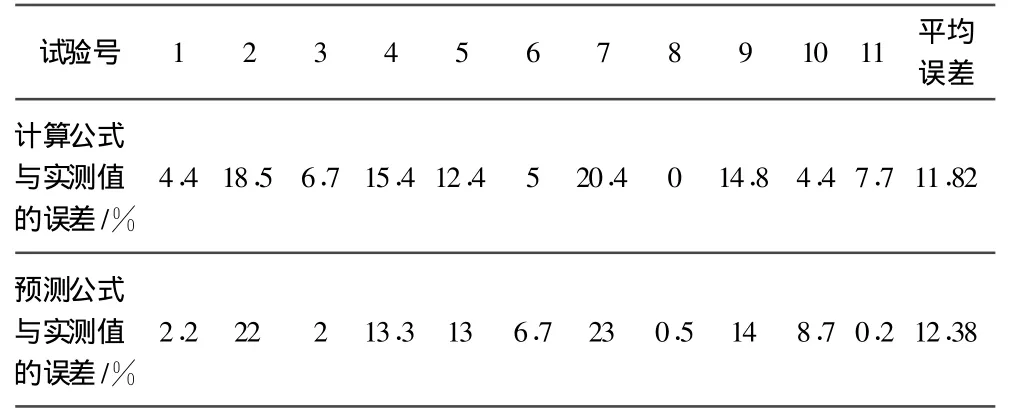
表2 筒蓋最大載荷力矩經驗公式計算結果與實測結果對比Tab.2 Comparison of themaximal moment on the hatch of experience formula and test data

從表1和表2可以看出,預測公式得到的均方差σ要比計算公式得到的大。也可以說從總體上看,計算公式要比預測公式得到的結果精確,但從均方差來看,二者相差較小。

4 結 語

從均方差可以看出,以上推導的2種公式得到數值與實測值誤差很小,計算公式能較為精確、方便地計算筒蓋所受的最大載荷及力矩,預測公式也能在發射前很好地預測筒蓋所受的最大載荷及力矩。

[1]倪火才.潛地導彈發射裝置構造[M],哈爾濱:哈爾濱工程大學出版社,1998.

[2]武漢測繪學院最小二乘法教研組,最小二乘法[M].北京:中國工業出版社,1985.

[3]郭祿光,等.最小二乘法與測量平差[M].上海:同濟大學出版社,1985.

[4]方家范.筒口壓力場的試驗研究[A].中國兵工學會應用力學研究會學術交流會,1987.

[5]黃壽康,王玉堂,等.流體動力·彈道·載荷·環境[M].北京:宇航出版社,1991.

[6]景思睿,張鳴遠.流體力學[M].西安:西安交通大學出版社,2001.

[7]BARMES R A.Explosives Engineering[Z].No3,1998.

[8]GOKALP I,BODELE E,COUSTY R,et al.Modeling Droplet Break-up Effects ForHigh-PressureCryogenic Spray Combustion Codes[R].AIAA-2000-3496.