基于水聲信號的瞬時頻率估計算法

張 靖

(大連測控技術研究所,遼寧 大連 116013)

0 序言

在許多實際的信號處理應用中,估計一個非平穩時變過程的瞬時頻率(Instantaneous Frequency,IF)意義重大。一些信息探測系統只要系統與目標之間有相對運動,就會產生“多普勒效應”,頻率會隨相對運動發生變化,傳播媒質的擾動也會使頻率變化,雷達、聲吶、移動通信、醫療設備和天文觀測等都存在這一問題。

目前針對瞬時頻率的估計方法的核心為概論統計,統計中所用的統計量,主要是樣本平均值或樣本函數算數平均值,它們具有最小方差性、無偏性等相當好的特性。然而樣本平均值的抗干擾性很差。為了獲得穩健統計解,發展了一種既保留所有數據,又削弱污染源對統計結果影響的統計方法,即 M-估計[1],其能獲得穩健性的瞬時頻率估計值。

目前對瞬時頻率的估計方法有很多,對于水聲信號受海洋聲場環境非常復雜、測量測備工作狀態不穩定、信噪比不足等因素的影響,很難獲得理想的瞬時頻率特征[2-5]。對于隨時間呈線性變化的非平穩信號來說,其穩健的瞬時頻率估計是必要的。研究分析水聲信號的瞬時頻率估計方法對實船噪聲特征頻率提取,輻射噪聲“多普勒效應”分析及噪聲源分析意義重大。本文提出一種綜合相位法和M估計方法獲得水聲信號的瞬時頻率,并利用計算機仿真分析研究該方法的效果。

1 相位差分方法

對于理想的信號,其離散水聲信號可以表示成r(n)=Aexp[jφ(n)]。

根據離散信息瞬時頻率定義,離散時間域對應為差分運算,即可得到離散時間瞬時頻率的估計。有3種相位差分算子[6],它們分別是前向有限差分、后向有限差分和中心有限差分,與這3種相位差分算子相對應的瞬時頻率估計見式(1)～式(3)。

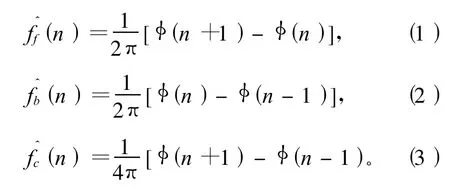
當信噪比很高時,利用中心差分法直接估計某特征頻率的瞬時頻率,得到的頻移特征曲線較平滑,誤差較小,精度高。

由于水聲信號容易受到干擾,單純地采用時刻Ti-1和Ti+1的相位估計Ti時刻的瞬時頻率,由于相位離散度大引起的瞬時頻率估計誤差也很大,很難準確估計瞬時頻率。由于通過較長的平均時間可以有效地抑制噪聲的影響,因為當噪聲服從高斯分布時,噪聲方差將隨著平均時間的增加而線性減小。因此在低信噪比情況下,增加有效觀測時間是提高同步性能的方法之一,從而采用長時間多點相位中心差分法。

根據Tayker公式可得:

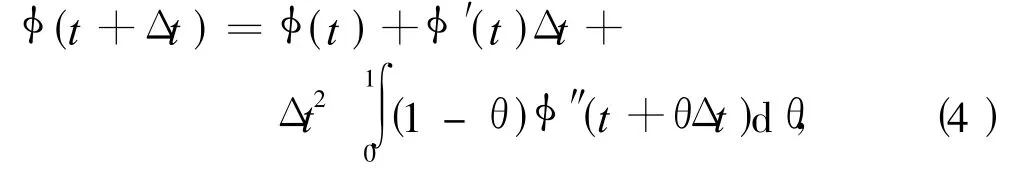
針對離散相位信息,分別取 Δ t=i,i+1;t=n0,則可得

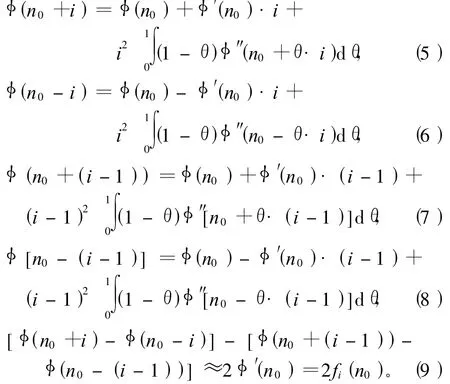
因此可近似得到 1組 2f1(n0),2f2(n0),…,2fi(n0)。

2 基于M-估計方法分析瞬時頻率

對于M-估計方法,核心是在穩健性和精確性的2個定量化泛函空間中,找出1個鞍點,即敏感性最差、精確性最好的解[6]。實際是取函數 ψ(x),解方程

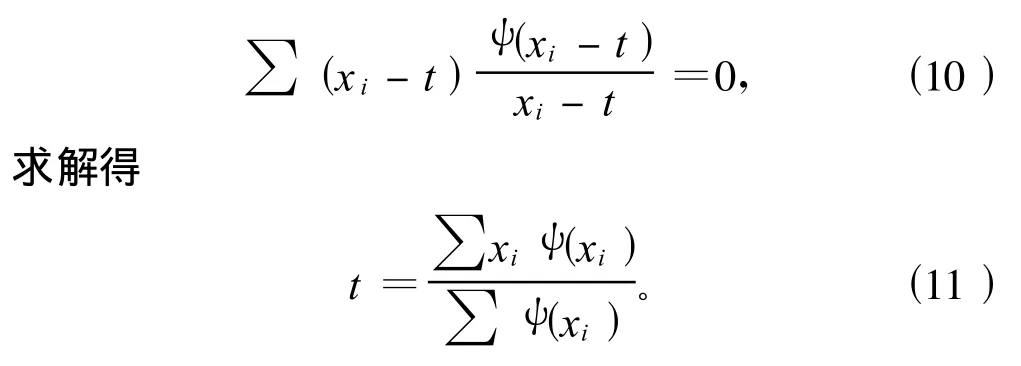
令wi=,則上式剛好寫成加權平均的形式t=∑xiwi,即形成自動加權的權函數平均形式。

通過求解方程可知,當滿足tn=tn-1時,tn-1為最優解。

依據估計準則的統計背景,M-估計可以分為3類[7]:一是基于概率密度(或誤差分布)的M估計,如最小二乘估計等;二是與概率密度無關的M估計(經驗方法),權函數通過數值模擬獲得,而無須顧及是否知道誤差的概率密度,如丹麥法等;三是基于隨機模型驗后估計的穩健估計,如李德仁選權迭代法。在參數回歸估計中,不同的權函數形式產生了不同的估計方法。為了實現參數估計的穩健性,一般遵循大誤差以小權,小誤差以大權,等價權公式可以通過數值模擬經驗確定的原則。等價權是殘差的函數,參數的迭代求解中殘差的改變引起等價權的改變。本文采用的權函數[8]為:

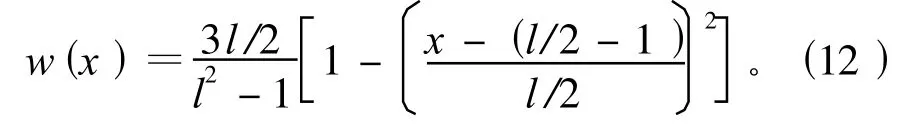
3 仿真分析

本文通過仿真模擬不同信噪比下水下目標勻速直線運動產生的單頻線譜輻射噪聲,分析其由于多普勒效應產生的瞬時頻率特征。

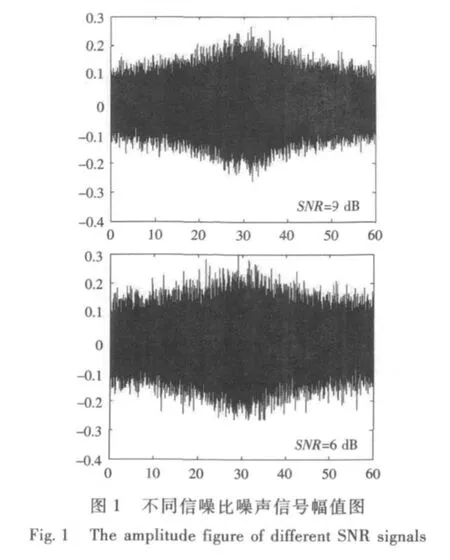
仿真數據:信噪比分別為6 dB和9 dB;信號頻率100 Hz;采樣時間60 s;目標速度6 m/s;目標最近距離30 m;其建立的仿真信號如圖1所示。

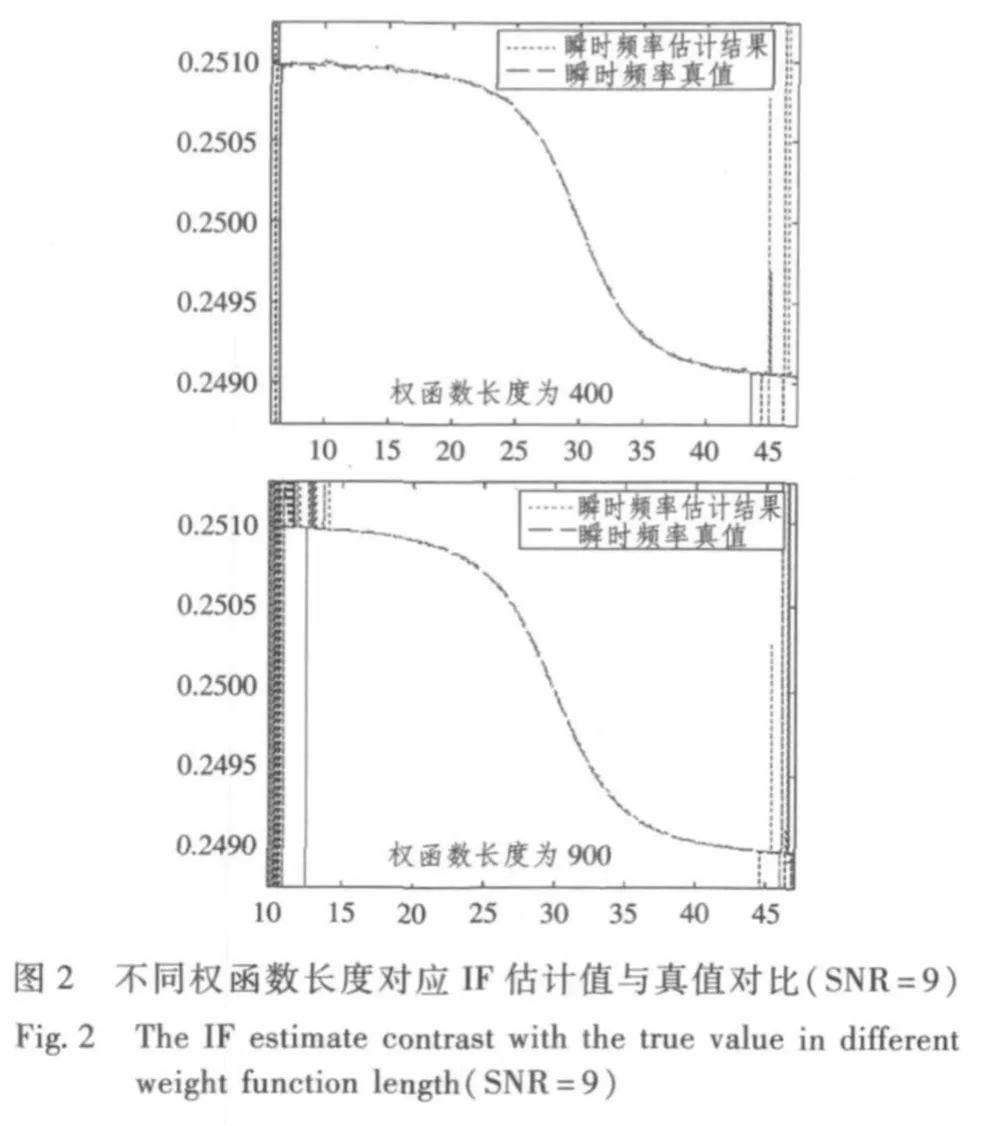
對仿真建立的信號分別采用不同長度的權函數進行分析,其結果如圖2和圖3所示。

通過上圖可以看出,對于同1組噪聲信號,權函數的長度越長,其瞬時頻率估計值越接近真值;對比不同信噪比的噪聲信號,采用相同權函數長度分析情況下,信噪比越高,瞬時頻率估計值越理想。同時應該指出,該方法權函數長度越長,要求的噪聲數據量越大,因此計算量大耗時較長,一般適合對信號的后續分析,不適合對信號的實時跟蹤。

4 結 語

本文通過研究建立了一種穩健的瞬時頻率估計方法,通過計算機仿真分析,研究了不同信噪比、不同權函數長度對瞬時頻率估計的影響。綜合分析表明,該方法能有效的估計運動目標速度較低情況下產生的瞬時頻率。

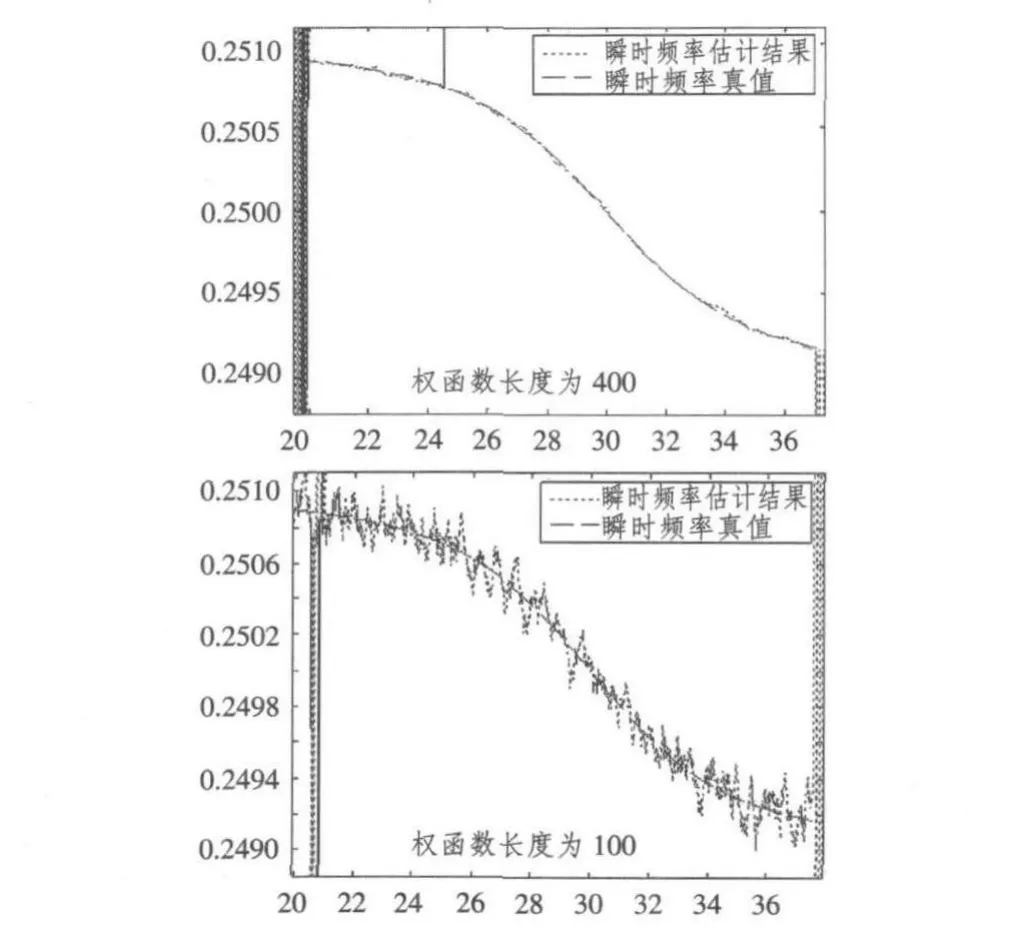
圖3 不同權函數長度對應IF估計值與真值對比(SNR=6)Fig.3 The IF estimate contrast with the true value in different weight function length(SNR=6)

[1]王安幫,等.M-估計的權函數選取及其抗差性比較[J].北京測繪,2008,10(1):8-10.WANG An-bang,et al.Selection of M-estimated weight functions and robust comparision[J].Beijing Surveying and Mapping.2008,10(1):8-10.

[2]李紅娟,孫超.水聲通信自適應多普勒頻移補償仿真研究[J].計算機仿真,2007,24(2):302-304.LI Hong-juan,SUN Chao.Adaptive doppler compensation forunderwateracousticcommunication[J].Computer Simulation,2007,24(2):302-304.

[3]李君橋,等.基于多普勒頻移的水下運動目標測距技術[J].聲學技術,2008,27(5):758-760.LI Jun-qiao,et al.Passive ranging of underwater motional targets based on Doppler frequency shift[J].Technical Acoustics,2008,27(5):758-760.

[4]莊曉明,等.基于多普勒頻移的水下超聲探測目標回波信號處理方法[J].艦船電子對抗,2008,31(6):88-91.

[5]DJURIC P M,KAY S M.Parameter estimation of chirp signals[J].IEEE Transactions on Acoustics,Speech and Signal Pro2 cessing,1990,38(12):2118-2126.

[6]孫曉奇.非平穩信號瞬時頻率估計[D].碩士論文,2009.

[7]王文軍.極大似然估計的穩健改進[J].武漢工業學院學報,1990,(4):35-41.

[8]黃曉紅,等.改進的相位展開算法及其在瞬時頻率估計中的應用[J].電子學報,2009,(10):2266-2272.