談高中數學“新定義”題型的解題策略

510080 廣州市第七中學 劉 紅

談高中數學“新定義”題型的解題策略

510080 廣州市第七中學 劉 紅

在近幾年全國、各省的高考數學命題中，“新定義”問題越來越受到關注和重視.所謂“新定義”問題，是相對于高中教材而言，指在高中教材中不曾出現過的概念、定義.它的一般形式是：由命題者先給出一個新的概念、新的運算法則，或者給出一個抽象函數的性質等，然后讓學生按照這種“新定義”去解決相關的問題.“新定義”問題總的來說題型較為新穎，所包含的信息豐富，能較好地考查學生分析問題、解決問題的能力.掌握好下列幾種解題的思路與方法，為我們在宏觀上把握這類題型提供了思維方向.

1 有關定義“集合的問題”

有關定義“集合”的問題，可化歸為對集合中元素特征的研究.

例 1 若規定 E={a1，a2，a3.…a10}的子集{ai1，ai2，…ain}為E的第k個子集，其中k=2i1-1+2i2-1+…+2in-1，則：

(1){a1，a3}是 E 的第_____個子集;

(2)E的第211個子集是______.

分析 此題把E的所有子集進行了“編號”，編號k的值可按表達式的要求計算.故(1)中k=21-1+23-1=5;(2)首先要對編號211進行估計分析：參考27=128，可確定指數的范圍，容易得到答案{a1，a2，a5，a7，a8}.此題弄清元素的下標數字特征對k值的貢獻是解題的關鍵.

例3 設S為實數集R的非空子集.若對任意x，y∈S，都有 x+y，x-y，xy∈S，則稱 S 為封閉集.下列命題：

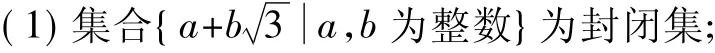
(2)若S為封閉集，則一定有0∈S;

(3)封閉集一定是無限集;

(4)若S為封閉集，則滿足S?T?R的任意集合T也是封閉集.

其中的真命題是________.(寫出所有真命題的序號)

分析 封閉集對集合中元素的特征提出了明確的要求，故只需從元素的特征入手解答.易知(1)為真命題;(2)由“若對任意 x，y∈S，都有 x+y，x-y，xy∈S”，若集合 S 為{x，y，…}，則集合 S 可以“擴張”為{x，y，x+y，x-y，xy…y-x，}，故 S 必然可再次“擴張”為{0，x，y，…}，故0∈S，此命題為真命題.(3)可由(2)中得到啟示，舉反例S={0}，故為假命題.(4)借助反例S={0}易知T{0，1}不符合“封閉集”的概念，故為假命題.

2 有關定義“運算”的問題

有關定義“運算”的問題，在理解運算法則的基礎上，試圖去尋求運算規律，并進行合情推理.

例4 設S是至少含有兩個元素的集合.在S上定義了一個二元運算“*”(即對任意的a，b∈S，對于有序元素對a，()b，在S中有唯一確定的元素a*b與之對應).若對任意的 a，b∈S，有 a*(b*a)=b，則對任意的a，b∈S， ┈┈┈下列等式中不恒成立的是

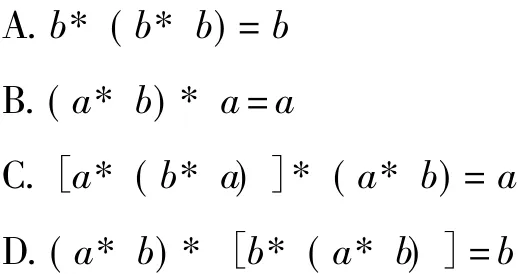
分析 新定義的運算法則是a*(b*a)=b，故應重點去理解這個運算法則和運算結果特征.易知，B選項中(a*b)*a=a與已知運算法則中所體現出的結構不同，可變形為：(a*b)*［b*(a*b)］，再結合運算規律，知運算結果應為b.故選B.

例5 對于大于1的自然數m的n次冪，可用奇數進行如圖所示的“分裂”，仿此，記53的“分裂”中的最小數為a，而52的“分裂”中的最大數為b，則a+b= ___.

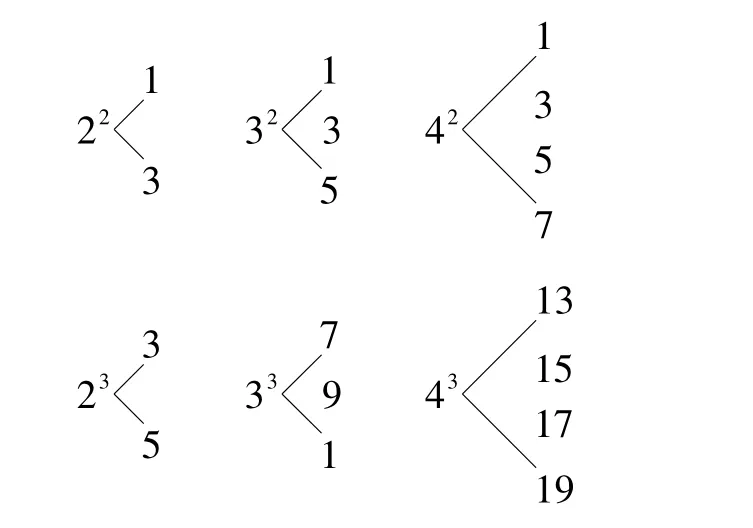
分析 在這種“分裂”運算中，通過觀察分析，可以進行合情推理，尋求其“分裂”的規律，x2型“分裂”從上到下是連續的奇數，x3型分裂從左到右也是連續的奇數，故52的“分裂”為1，3，5，7，9，故b=9，53的“分裂”為21，23，25，27，29，故 a=21，所以答案為 30.

3 有關抽象函數的問題

3 有關抽象函數的問題，通常是抓住函數特性在定義域上是恒等式，利用變量代換解題，即利用“賦值法”尋求函數的有關性質，如周期性、奇偶性、單調性等.

例7 設f(n)為正整數n(十進制)的各數位上的數字的平方之和，比如f(123)=12+22+32=14，記f1(n)=f(n)，fk+1(n)=f(fk(n))，k=1，2，3，…，則 f2006(2006)的值為

分析 利用題目定義的運算關系，先算幾個數(或幾步)看看，試圖從中找到相關的規律，是我們常用的方法.將f(2006)=40記做2006→40，于是有：

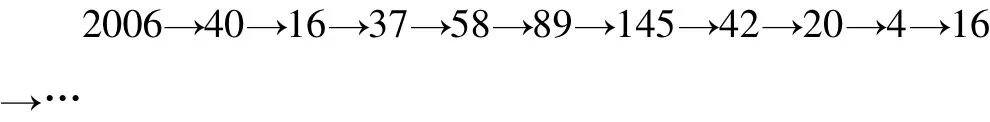
從16開始，fn是周期為8的周期數列，故有：

f2006(2006)=f2004(16)=f4+250×8(16)=f4(16)=145.故選D

例8 已知函數y=f(x)的定義域為R，且對于任意a，b∈R，都有 f(a+b)=f(a)+f(b)，且當 x＜0 時，f(x)＜0恒成立，f(3)=-3，證明：函數y=f(x)是R上的減函數;

證明：函數y=f(x)是奇函數;

試求函數 y=f(x)在［m，n］上的值域(m，n∈Z).

解 根據所要證明的問題，采用有向思維，通過賦值和變量代換，應該可以得到所需的結論.

故函數的值域為［-n，-m］.

20111103)