印染車間中深淺顏色坯布切換算法模型的實現

胡 穎，周曉慧

杭州電子科技大學信息與控制研究所， 浙江杭州 310018

0 引言

生產過程中的優化調度一直是過程操作中的關鍵問題，提高生產車間的生產管理水平和生產效率，確保準時交貨，對提高企業的市場競爭力具有迫切的現實意義。而當前國內印染企業的生產調度大部分還是由人工來完成，人工調度工作量大、效率低、實時性差，很難適應市場多品種、小批量的生產要求[2]。理論研究方面，現有的印染調度模型對深淺顏色坯布的切換時間考慮甚少，難以應用于實際。本文研究染色工藝的優化調度，通過改進現有模型建立合理的考慮深淺顏色坯布切換時間的優化調度模型，使得模型的使用面更加廣泛，更加實用于實際生產過程。

1 優化調度模型

本節中我們將根據印染批處理生產調度的多產品、多工序、順序加工等調度模型特點，給出基于連續時間MILP數學調度模型的約束條件[1-3]。其中約束（1）-（6）都是現有模型的約束[2]，（7）-（9）是改進完善后考慮深淺坯布切換時間的約束。在模型的約束條件中，調度模型主要的決策變量分別是Xijl、Wiu和Siu。它們分別表示一道工序上是否是相鄰訂單、生產設備上的訂單分配和生產設備上的第一個加工的訂單分配。

1.1 模型約數函數

1） 在工序上l相鄰加工的訂單u和v必定分配給同一臺生產設備上加工：

2）在工序l中，生產設備u上除最后加工生產的訂單外其余所有訂單都有且僅有一個唯一的直接后序訂單：

3） 在工序l中，生產設備u上除了第一個被加工的訂單外其余的每個訂單都有且僅有一個唯一直接前序訂單：

4）模型中主要決策變量Wiu和Siu的關系：

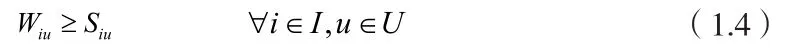
5）在生產設備u上至多有一個初始加工的訂單，其中訂單集合中的唯一一個訂單i是第一個被加工的訂單，此時：

6）每道工序中任意一個訂單必須分配并只能分配給一臺唯一的生產設備加工：

7）當一個訂單i的生產工序m是在生產工序l前面的，則有此訂單i在工序l中的起始時間必須大于或等于此訂單i在工序m中加工完成后的時間：

8）同一道工序上兩個具有直接前后續關系的深淺訂單j中后序訂單的起動時間大于等于訂單i在生產設備u上的加工運行時間與此工序設備u上訂單i和訂單j切換所需時間即Ciju的和。式中M為足夠大的正數，保證訂單j和訂單i在工序l為直接前后序訂單：

9）訂單的實際延期是指訂單的完成時間和訂單的交貨期的Di差值：

1.2 模型目標函數

為了降低成品生產后的高額庫存成本以及減少企業的流動資金，印染行業對印染訂單交貨期的準時要求非常嚴格。本調度模型的目標函數是使訂單在最大限度的接近訂單交貨期：

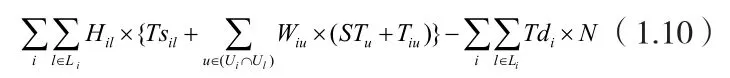
調度模型中所求的最優調度解的目標就是使得目標函數式（1.10）取到最大值。式中的N是個足夠大的參數，這樣就迫使訂單的延期總是最小；而參數Hil是用來區分在最后工序中各訂單執行的優先后次序的，此參數是由Pinto和Grossmann（1995）[3]提出來的：

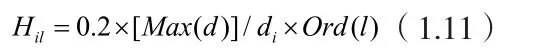
式中Max( d )指的是印染生產中所有被調度的訂單的交貨期的最大值，而Ord( l )指訂單生產工序的工序號。

2 模型求解與結果分析

印染生產是一種將原材料轉化為產品的增值生產，原材料為坯布以及染化料、燒堿雙氧水等一些印染助劑，產品為面料。整個印染工藝基本過程分為前處理、染色和后整理[2-3]，不同的訂單產品由于生產加工的坯布不同一般有著各自特定的工藝和工序路線，其中印染工序上深淺顏色訂單的切換時間是批處理生產調度問題中必須要考慮的一個重要方面[1-2]。表1給出了印染生產的工序流程和每道工序包含的設備號。在印染車間坯布加工生產中，假設每道工序都只包含一臺設備，對應的設備號就是工序號。

工序號 工序名 包含的設備號1翻縫、燒毛 1 2退漿、煮練、氧漂 2

表1 印染生產設備信息

訂單的基本信息包含了坯布類型，坯布顏色，坯布長度，訂單的交貨期，見表2。

表2 訂單的相關信息

表3 訂單相互之間的切換時間（有直接前后序關系時）

實例中四個訂單相互之間的如果有直接前后序時的切換時間見表3。此表說明在工序7即染色工序上，由于訂單1是石頭色的全棉帆布，在四個訂單中顏色最淺，所以當其他訂單作為訂單1的后續訂單時，機床不用清洗，切換時間都為0；訂單2是藏青色的全棉府綢，在遇到黑色的訂單3時不用清洗，因為黑色是更深的顏色，而后續訂單是石頭色的訂單1和灰色的訂單4時則

需要清洗，清洗時間分別為13個小時和10個小時；訂單3和訂單4同理。

將實例訂單數據以及印染生產車間的生產相關數據以ILOG OPL的語義形式導入工程中的數據文件，然后運行模型求出實例的調度結果集，最后根據其調度結果集繪制出實例的生產甘特圖，如圖1所示，甘特圖清晰的顯示出運用模型后調度的結果。

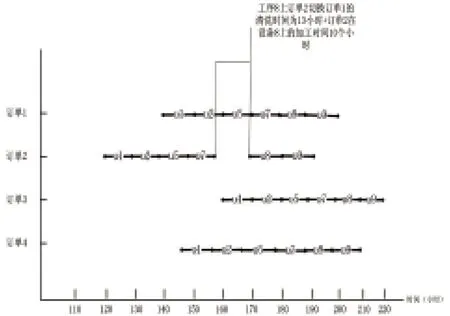
圖1 運行結果甘特圖

3 結論

本文著重針對印染生產中的染色環節生產工藝進行研究，在現有模型的基礎上，充分考慮深淺坯布切換，建立了考慮深淺坯布切換時間的優化調度模型，將數學模型轉換為ILOG CPLEX的可求解模型，用ILOG的CPLEX求解該模型，驗證了該模型的有效性和可行性。

[1]鄭俊玲.基于連續時間MILP批處理調度研究以及在印染行業的應用[D]，2008：30-33.

[2]梅紅，張智豐.基于連續時間的生產過程優化調度[J].浙江大學學報，2010：1423-1427.

[3]Gooding W.B.，Pekney J.F.，McCroskey P.S.，Enumerative Approaches to Parallel Flowshop Scheduling via Problem Transformation[J].Computers and Chemical Engineering，1994，18：909-920.