淤堵試驗中“駝峰”形 k～t曲線形成的影響因素分析

付長生,趙 堅,沈振中,杭學軍,張 松

(1.河海大學水利水電學院,江蘇 南京 210098;2.江蘇省交通規劃設計院股份有限公司,江蘇 南京 210005;3.揚州市勘測設計研究院有限公司,江蘇 揚州 225009)

工程實例表明,作為反濾材料的土工織物若選擇不當,使用過程中容易產生淤堵,影響反濾效果。為保證土工織物的反濾效果穩定、持續、有效,可以通過土工織物與被保護土的淤堵試驗對土工織物進行選型。筆者通過分析多組土工織物淤堵試驗所獲得的滲透系數(k)與時間(t)的關系曲線發現,在淤堵試驗初始階段,存在明顯的 “駝峰”形k～t關系(圖1),即包含被保護土和土工織物的透水體的滲透系數在試驗初期隨時間逐漸增大,經過一段時間到達峰值后逐漸減小并趨于某一固定值。文獻[1-2]對淤堵試驗的“駝峰”現象有過描述,但只作了簡單解釋,未見深入分析。筆者將以試驗為基礎,通過多因素綜合分析,探討“駝峰”產生的原因,分析影響k～t曲線峰值kmax、峰值出現時間T1和持續時間T2的主要因素及其敏感性。

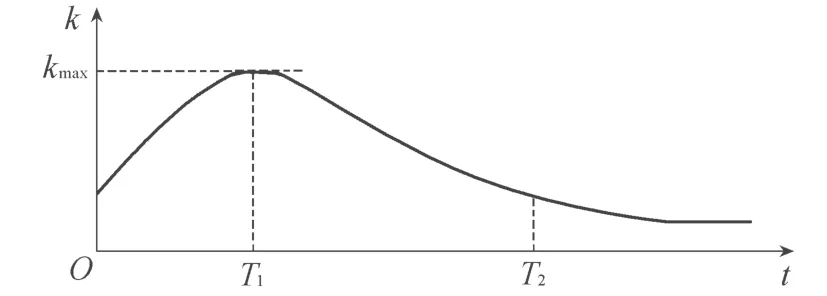
圖1 k～t曲線

1 試驗模型及試驗方案

1.1 試驗原理

淤堵的過程是滲透系數逐漸變化并最終趨于某一定值的過程,本質上是滲透變形的一種特殊情況。因此,可以參照達西滲透試驗原理設計土柱模型進行室內淤堵試驗。

1.2 試驗模型

土柱模型試驗是土工織物淤堵試驗研究中最常用的方法,也是最簡單有效的方法。筆者采用此方法,利用循環水測試系統分別采用短筒及改進的長筒模型進行室內模型試驗。

短筒模型參照SL 237—1999《土工試驗規程》中常水頭70型滲透儀的原理制作而成,一般試驗土樣高度為8cm。改進長筒模型是在文獻[3]推薦的長筒模型基礎上,針對本文研究需要加長試驗筒柱并沿筒柱增設測壓管口(間隔25mm)。改進的模型筒由模型筒身、有機玻璃蓋、鋼筋吊緊螺栓等部分組成,筒身直徑為10 cm,高度為80 cm,模型筒身選用有機玻璃制作。改進的長筒模型示意圖見圖2。

圖2 改進的長筒模型示意圖

1.3 試驗流程

試驗時,按不同干密度、顆粒級配及細粒質量分數拌制土樣,并裝填到模型筒中,在土樣出水端鋪墊選定的土工織物。模型筒試樣從上到下分別為礫石層、粗砂層、土樣(改進長筒模型中土樣高度為20cm,分別標記Ⅰ～Ⅷ層)、土工織物、粗砂層、礫石層。進水方式自上而下。裝樣完成后,進行土樣飽和及排氣程序。飽和排氣時由模型筒下部進水,需控制水頭緩慢增加,直至飽和排氣完成。此過程一般耗時較長,約24h以上,飽和過程中氣泡由下至上冒出,經上部排氣閥排出。隨后,逐步增加水頭至合適值,觀察測壓管水頭高度,維持穩定后開始測試,主要測量各觀察點測壓管水頭高度和試樣過水流量,并計算對應的滲透系數。當所測試樣滲透系數隨時間趨于一個穩定值時,試驗結束。

1.4 試驗方案

初期試驗及相關文獻表明,影響淤堵試驗滲透系數“駝峰”形態的因素主要是外荷載、土工織物及土體三大類,本文據此選用水頭、土工織物單位面積質量、細粒質量分數、顆粒級配和干密度5個因素。用正交試驗方法,選擇 L18(21×37)正交表,設計了18組典型試驗工況來研究多因素對k～t曲線“駝峰”形態的影響。各試驗工況考慮了各個因素的不同水平值,以及土工織物單位面積質量分別與水頭和細粒質量分數的交互作用(表1)。

表1 正交試驗因素及水平

改進長筒模型試驗分別選擇了300 g/m2和500g/m2的土工無紡布對同一土樣進行對比試驗,主要研究土樣各層土體顆粒及不同規格土工織物對滲透系數的影響。

2 “駝峰”現象及其影響因素分析

2.1 短筒試驗k～t曲線上的“駝峰”現象

在試驗過程中,內部土體未發生滲透變形,只是試樣的滲透系數發生了一定幅度的變化。圖3、圖4描繪了18組典型試驗工況所獲得的短筒試樣淤堵試驗k～t曲線,其中圖 3為相對低水頭(水頭差1m)的1～9工況的k～t曲線,圖4為相對高水頭(水頭差2m)的10～18工況的k～t曲線。由這2幅圖可見:①各工況組試驗k～t曲線均具有“駝峰”特征,且“駝峰”現象持續時間都在200h以上,說明在整個淤堵過程中材料存在相當長一段時間的高滲透性階段。②各工況的駝峰峰值點左側曲線斜率比右側曲線斜率大,說明在淤堵初期材料的滲透系數會較快增大。k隨t變化的宏觀趨勢為先升后降,但在各時段內呈現階段性凸凹起伏變化,這一點在1～9工況中更顯突出,10～18工況的較高水頭削弱了階段性的凹凸變化。③各工況的“駝峰”峰值出現時間有差異,持續時間約為峰值前的1.3倍。峰值出現時間最長的84h和最短的53h分別發生在水頭相對低的工況4和相對高的工況10。④各工況的“駝峰”峰值比滲透系數初始值及最終穩定值大,不同水頭情況存在差異,1～9工況峰值約為初始值的5～10倍,是最終值的10～20倍;10～18工況峰值分別為初始值和最終值的10～20倍及 20～50倍,其中較大的峰值區在工況10～18下出現,說明高水頭對峰值影響較大。⑤1～9工況的“駝峰”平均持續時間比工況10～18的長,說明低水頭更易延長“駝峰”的出現時間及持續時間。

2.2 “駝峰”現象影響因素分析

圖3 淤堵試驗 k～t曲線(工況1～9)

圖4 淤堵試驗 k～t曲線(工況10～18)

由圖3和圖4可見,各典型工況試驗都出現了“駝峰”形k～t關系曲線,且各工況“駝峰”曲線的峰值kmax、峰值出現時間T1及峰值持續時間T2存在差異。下面將以此三要素作為考察指標,對試驗結果進行綜合分析。

2.2.1 單指標方差分析

按照正交試驗方差分析方法,求得考察指標kmax,T1及T2的偏差平方和,進行F值檢驗,判斷各因素的顯著性,并通過顯著性檢驗得到各因素的敏感性關系。

由單指標kmax方差分析結果可知,除細粒質量分數不顯著外,其他因素都是顯著或者高度顯著因素,說明除細粒質量分數外,其他因素都或多或少地對峰值產生影響。F值確定顯著性由大到小的排列順序為:X1,X4,X2,X2×X3,X1×X2,X5,X3。

指標T1的方差分析結果表明,水頭因素為高度顯著因素,細粒質量分數及顆粒級配因素均為不顯著因素,其他因素均為顯著因素。各因素的 F值差異較大,高度顯著因素的F值為顯著因素的3倍多,說明在T1單指標考察中,水頭影響占據絕對地位。F值確定由大到小的顯著性排列為:X1,X5,X2×X3,X1×X2,X2,X4,X3。

各因素對T2指標的影響中,水頭為高度顯著因素,水頭與土工織物單位面積質量的交互作用和干密度為顯著因素,細粒質量分數、顆粒級配為不顯著因素,F值確定由大到小的顯著性排列為:X1,X5,X1×X2,X2×X3,X2,X4,X3。除一般顯著因素外,最顯著和不顯著因素與T1指標的方差分析結果相近。

2.2.2 多指標方差分析

多指標分析的思路是“化多為單”,由于本試驗的3個指標的影響權重不確定,宜采用回歸評分法“化多為單”。首先進行經驗打分,再利用 Excel的linest函數計算三元函數回歸分析,得到回歸系數及相應統計量,根據回歸方程獲得回歸得分。

經計算,得回歸方程為

根據此方程計算回歸得分,即綜合指標,對綜合指標進行方差分析。由方差分析結果(表2)可知,水頭與土工織物單位面積質量的交互作用對綜合指標的影響最大,為高度顯著因素;土樣干密度、水頭、細粒質量分數與土工織物單位面積質量的交互作用為顯著因素;影響最小的是細粒質量分數和顆粒級配,為不顯著因素。

表2 綜合指標的方差分析結果

綜上所述:①“峰值”現象反映的是滲透系數波動變化過程,滲透系數波動主要由顆粒移動導致的土樣結構變化引起,這種結構變化會隨著時間推移并在無新的外力作用下趨于平衡狀態,使滲透系數波動較小直至穩定;②水頭是單因素分析中影響最顯著的因素,水頭作為滲透水流的直接驅動力是導致土顆粒移動的主要因素;③土樣干密度、顆粒級配等為顆粒移動提供了客觀條件,但如果缺少外加荷載的作用,不論顆粒級配如何,不論干密度如何變化,顆粒也不會產生運動;④指標T1,T2受各個影響因素的影響幾乎是一致的,說明峰值的出現時間越遲,峰值持續時間也越長。

3 “駝峰”現象產生的原因

3.1 長筒試驗各層的“駝峰”現象

圖5為300g/m2和500g/m2土工織物長筒試驗土柱各段的k～t曲線。由圖5可見,土樣最上2層(Ⅶ層、Ⅷ層)的滲透系數最大,達到5.0×10-5cm/s左右,為整體滲透系數的2倍左右。土樣中部Ⅳ層、Ⅴ層、Ⅵ層的滲透系數最小,與上部Ⅶ層、Ⅷ層的滲透系數相差近1個數量級。其他分段土層的滲透系數較接近,這在500g/m2的試驗組中反映較明顯?？梢?組試驗土樣中都出現了3個滲透系數分層化區域。滲透系數變化的總體規律是兩端最大、中間最小。

選擇500g/m2土工織物試驗組的數據,將3個分層化區域的滲透系數變化情況繪成曲線,見圖6,可見,每個分層化區域的滲透系數也都存在“駝峰”現象,且以土樣上下2端區域最明顯。

圖5 土樣各土層 k～t曲線

圖6 土層上、中、下各部分及整體k～t曲線

3.2 原因分析

通過上述對試驗數據的分析,認為引起“駝峰”現象的主要原因是試樣兩端進出水口附近的土體受到水體流動引起的不平衡力及不平衡力矩較大,其中較細的土顆粒在滲透力拖曳下容易發生不規則移動,甚至隨水流流出土體,從而改變了該區域土層的結構,使得滲透系數發生變化。而這種現象也在土樣內部發生,只是這里的土樣結構在兩端土體的“制約”下受到的不平衡外力較小,引起的顆粒移動也較少,土層結構變化波動幅度相對較小。每一層土樣或多或少地發生結構性改變,表現為滲透系數變化,最后集中表現為土樣整體滲透系數的“駝峰”現象?？梢?土工織物淤堵試驗過程中形成的滲透系數與時間的“駝峰”現象來自土樣細顆粒移動引起的土樣和土工織物內部過水通道結構變化,且這種變化經過一定時間調整后會逐漸趨于穩定。

長筒試驗相對短筒試驗而言是一種“放大”,目的是探明究竟是哪一層土性質的變化引起了“駝峰”現象,兩者試驗結果是一致的。試驗結果分析表明:對特定的試驗土樣,試驗時為減小“駝峰”現象的影響,可以降低試驗水頭,在實際工程中,特別是新建初次使用的防滲工程,需要注意蓄水過程及防滲體的顆粒級配、干密度等。

4 結 語

土工織物淤堵試驗過程中形成的滲透系數與時間的“駝峰”現象受到水頭、土工織物單位面積質量、細粒質量分數、顆粒級配、干密度等因素的影響。其中,水頭、顆粒級配及干密度影響最大。顯然本文討論的現象在實際工程中亦可能發生,特別是新建的反濾工程。從防止滲透變形和減少淤堵的角度看,應在設計和施工等環節考慮避免出現“駝峰”高峰值和縮短其出現期的措施。

:

[1]WU C S,HONG Y S,YAN Y W,et al.Soil-nonwoven geotextile filtration behavior under contact with drainage materials[J].Geotextiles and Geomembranes,2006(24):1-10.

[2]劉建華,郭忠印,丁志勇,等.公路土工合成材料淤堵試驗方法研究[J].公路交通科技,2004(7):33-37.

[3]王釗,陸士強.土工織物濾層淤堵標準的探討[J].水力發電學報,1991(3):55-63.

[4]FAURE Y H,BAUDOIN A,PIERSON P,et al.A contribution for predicting geotextile clogging during filtration of suspended solids[J].Geotextiles andGeomembranes,2006(24):11-20.

[5]方開泰.正交與均勻試驗設計[M].北京:科學出版社,2001.

[6]陶同康.土工合成材料與堤壩滲流控制[M].北京:水利水電出版社,1999.

[7]佘巍,陳輪,王釗.土工織物梯度比試驗研究的新進展[J].長江科學院院報,2006(2):58-60.

[8]ENNION M P,ALINE F N R,MARIA L G R,et al.A study on biological clogging of nonwoven geotextiles under leachate flow[J].Geotextiles and Geomembranes,2008(26):205-219.

[9]陳星柏.關于土工織物反濾層的滲透準則[J].水利學報,1990,21(9):47-51.

[10]GB50290—1998 土工合成材料應用技術規范[S].

[11]孔麗麗,陳守義.武山尾礦壩無紡土工織物濾層化學淤堵問題初探[J].巖土工程學報,1999,21(4):444-449.

[12]FISCHER G R,MARE A D,HOLTZ R D.Influence of procedural variables onthe gradient ratio test[J].Geotechnical Testing Journal,1999(22):22-31.