布朗單增量“快點(diǎn)”集的Packing維數(shù)

邱志平，林火南

（1.華僑大學(xué)數(shù)學(xué)科學(xué)學(xué)院，福建泉州362021；2.福建師范大學(xué)數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院，福建福州350007）

布朗單增量“快點(diǎn)”集的Packing維數(shù)

邱志平1，林火南2

（1.華僑大學(xué)數(shù)學(xué)科學(xué)學(xué)院，福建泉州362021；
2.福建師范大學(xué)數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院，福建福州350007）

討論布朗單樣本軌道的重分形分析問題，通過構(gòu)造一個(gè)上極限型分形集的方法，得到其不同的增量形式“快點(diǎn)”集的Packing維數(shù)結(jié)果.當(dāng)T＞0，0≤α＜1，ET（α）時(shí)，有Dim（ET（α））＝N，Dim（FT（α））＝N，Dim（GT（α））＝N，a.s..當(dāng)0＜α＜1時(shí)，ET（α），F(xiàn)T（α）和GT（α）的Hausdorff維數(shù)與其Packing維數(shù)不相等.關(guān)鍵詞： 布朗單；“快點(diǎn)”集；Packing維數(shù)；重分形分析

布朗單作為布朗運(yùn)動在多指標(biāo)情形的自然發(fā)展形式，在多指標(biāo)隨機(jī)過程研究中最具重要性和典型性，已得到了許多結(jié)果［1－6］.重分形分析的目的在于更加細(xì)膩地量化幾何測度的奇異結(jié)構(gòu).文［4］得到了布朗單的重對數(shù)律和一致連續(xù)模，文［5－6］在文［4］的基礎(chǔ)上更深入地研究了布朗單，討論那些使其重對數(shù)律不成立（即重對數(shù)律失敗）的所謂“快點(diǎn)”集合的重分形分析性質(zhì)，得到布朗單沿坐標(biāo)方向增量、局部增量和矩形增量3種增量形式“快點(diǎn)”集的Hausdorff維數(shù).本文與文［5－6］類似，進(jìn)一步探討布朗單樣本軌道的重分形分析性質(zhì).

1 預(yù)備知識

它表示［0，1］N中邊長為2－n，且其邊平行于坐標(biāo)軸的左閉右開N維立方體的集合.有時(shí)c表示分量同為常數(shù)c的向量，即c＝（c，c，…，c）.

其中：B（x，r）表示是以x為圓心，r為半徑的球.

顯然，φ－p＊（E）不是一個(gè)距離外測度，更不是測度［7］.經(jīng)過修正后，記

則φ－p（E）是一個(gè)測度，并稱φ－p（E）為E的Packing測度.定義E的Packing維數(shù)為

有關(guān)Packing測度和Packing維數(shù)的有關(guān)性質(zhì)，參見文［7］.

設(shè)W＝｛W（s）∶s∈RN＋｝是定義在（Ω，F(xiàn)，P）上的零均值的高斯過程，若滿足

2 主要結(jié)果及其證明

考慮布朗單沿坐標(biāo)方向增量“快點(diǎn)”集的Packing維數(shù).

定理1 設(shè)T＞0，0≤α＜1，ET（α）的表達(dá)式為

由式（2）可得，A?E1（α0），記Vn＝∪∞k＝nA0（k）.其中：A0（k）為A（k）的內(nèi)點(diǎn)集.對于固定m，I∈Mm，由文［9］中的式（2.3），存在正有限常數(shù)c1和c，使得當(dāng)n充分大且k≥n時(shí)，有

于是，有

從而由Borel－Cantelli引理，可得P（VnI＝?）＝0，因而Vn在［0，1］2內(nèi)幾乎處處稠密且為［0，1］2的開集，由引理1可得

定理得證.

考慮布朗單局部增量“快點(diǎn)”集的Packing維數(shù).

定理2 設(shè)T＞0，0≤α＜1，F(xiàn)T（α）的表達(dá)式為

則Dim（ET（α））＝N，a.s.

證明 僅對N＝2的情況證明，N＞2的情況類似可證得.設(shè)T＝1，α1∈（α0，1），δn＝n2－n（n≥1）.定義一族服從（0－1）分布的隨機(jī)變量序列｛ZI｝I∈Mn（n≥1）：對于I＝［（i，j）2－n，（i，j）2－n＋〈2－n〉），有ZI＝1，當(dāng)且僅當(dāng)

由布朗單的一致連續(xù)模結(jié)果［4］可知，幾乎處處地存在n0＝n0（ω），使得當(dāng)n≥n0（ω）時(shí)，對?I∈Mn，?s∈I，有

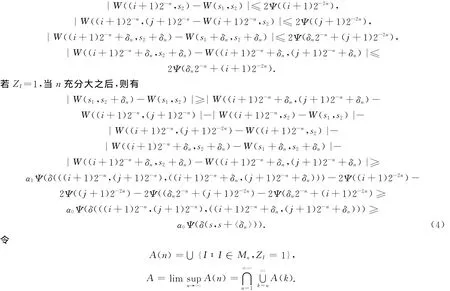
由式（4）可得，A?F1（α0）.記Vn＝∪∞k＝nA0（k），A0（k）為A（k）的內(nèi)點(diǎn)集.對于固定m，I∈Mm，由文［9］中的式（2.3），存在正有限常數(shù)c1和c，使得當(dāng)n充分大且k≥n時(shí)，則有

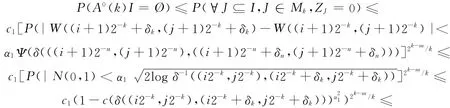
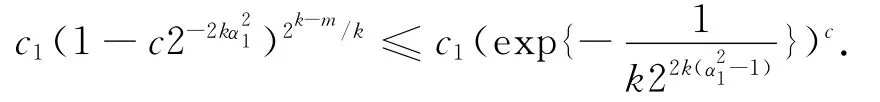
于是，有

從而由Borel－Cantelli引理，可得P（VnI＝?）＝0，因而Vn在［0，1］2內(nèi)幾乎處處稠密且為［0，1］2的開集.由引理得Dim（F1（α0））＝2，a.s.定理得證.

最后，給出布朗單矩形增量“快點(diǎn)”集的Packing維數(shù).

定理3 設(shè)T＞0，0≤α＜1，GT（α）的表達(dá)式為

則Dim（GT（α））＝N a.s.

證明 由文［6］定理2及引理1即可得.

［1］ EHM W.Sample function properties of mutli－parameter stable processes［J］.Z Wahrscheinlichkeitsheorie Verw Gebiete，1981，56（2）：195－228.

［2］ 林火南.Wiener單的局部時(shí)和水平集的Hausdorff測度［J］.中國科學(xué)：A輯，2000，30（10）：869－880.

［3］ KHOSHNEVISAN D，SHI Z.Brownian sheet and capacity［J］.Ann Probab，1999，27（3）：1135－1159.

［4］ OREY S，PRUITT N E.Sample function of the N－parameter Wiener process［J］.Ann Probab，1973，1（1）：138－163.

［5］ 黃群，林火南.布朗單樣本軌道的重分形分析［J］.福建師范大學(xué)學(xué)報(bào)：自然科學(xué)版，2003，19（2）：1－8.

［6］ 黃群.布朗單的矩形增量快點(diǎn)集Hausdorff維數(shù)［J］.莆田學(xué)院學(xué)報(bào)：自然科學(xué)版，2007，14（2）：34－37.

［7］ FALCONER K J.Fractal geometry－mathematical foundations and application［M］.New York：John Wiley ＆Sons，1990.

［8］ DEMBO A，PERES Y，ROSEN J，et al.Thick points for spatial Brownian motion：Multifractal analysis of occupation measure［J］.Ann Probab，2000，28（1）：1－35.

［9］ OREY S，TAYLOR S J.How often on a Brownian path does the law of iterated logarithm fail［J］.Proc London Math Soc，1974，28（1）：174－192.

Packing Dimension of“Fast Point”Sets for Brownian Sheet

QIU Zhi－ping1，LIN Huo－nan2
（1.School of Mathematical Sciencs，Huaqiao University，Quanzhou 362021，China 2.College of Mathematics and Computer Science，F(xiàn)ujian Normal University，F(xiàn)uzhou 350007，China）

The multifractal analysis for the sample paths of Brownian sheet is discussed in the paper.The packing dimensions of“fast point”sets with different increment forms of Brownian sheet are given by constructing a random fractals of limsup type.If T＞0，0≤α＜1，ET（α），then Dim（ET（α））＝N，Dim（FT（α））＝N，Dim（GT（α））＝N，（a.s.）.The Hausdorff dimensions of ET（α），F(xiàn)T（α）and GT（α）isn’t equal to their packing dimensions if 0＜a＜1.

Brownian sheet；“fast point”sets；packing dimension；multifractal analysis

O 552.1

A

（責(zé)任編輯：陳志賢 英文審校：張金順，黃心中）

1000－5013（2011）01－0109－04

2009－02－25

邱志平（1979－），男，講師，主要從事隨機(jī)過程理論及應(yīng)用的研究.E－mail：qzp＠hqu.edu.cn.

華僑大學(xué)科研基金資助項(xiàng)目（08HZR20）