雙參數(shù)威布爾分布在核電站數(shù)據(jù)處理中的應用

劉方亮，劉井泉，劉 偉

（1.清華大學 工程物理系，北京 100084；2.國家核電技術公司，北京 100029）

自1991年12月15日秦山核電站首次并網(wǎng)發(fā)電以來，我國核電已有近20年的運行經(jīng)驗。隨著運行時間的增加，電站的系統(tǒng)、構筑物和關鍵部件（SSCs）等出現(xiàn)不同程度的老化退化問題，需制定相應的電站維修更換策略，以保證電站能長期安全、經(jīng)濟地運行。設備部件失效數(shù)據(jù)的處理是制定以可靠性為中心的維修（RCM）和壽期管理（LCM）等維修策略的基礎。通過數(shù)據(jù)處理得到更準確的可靠性參數(shù)，是保證維修策略安全性和經(jīng)濟性的一個重要途徑［1］。

國內電站設備的可靠性參數(shù)一般通過行業(yè)通用數(shù)據(jù)和電站自身失效信息的融合處理來得到。由于核電站的非能動機械部件具有較長的設計壽命，在對運行積累的故障記錄進行處理的過程中會面臨一些問題，例如失效樣本過少、設備檢查信息不能直接被利用、維修引起的可靠度變化等。目前采用的統(tǒng)計學處理方法會帶來明顯的系統(tǒng)誤差，需要一種更為科學的方法進行處理。

本工作針對核電站失效數(shù)據(jù)處理過程中出現(xiàn)的問題，引入可修復系統(tǒng)模型和貝葉斯小樣本方法，綜合給出一種更為科學的處理核電站失效數(shù)據(jù)的流程。

1 核電廠常見設備失效數(shù)據(jù)

以國內某核電站定子冷卻水泵機械密封為例，通過整理某核電站4個機組8臺設備的工作票記錄，結合設備投運時間等信息可得到表1所列的失效統(tǒng)計結果［2］。

同傳統(tǒng)的可靠性試驗數(shù)據(jù)相比，核電站運行積累的失效數(shù)據(jù)有以下3個特點：1）每次故障記錄的起始時間不同、包含未發(fā)生故障的時間數(shù)據(jù)，單獨通過故障間隔時間來處理會丟失一部分信息；2）某一設備可能記錄到多次故障，需考慮故障間維修操作引起的可靠度變化而導致的數(shù)據(jù)分布不再獨立；3）失效次數(shù)較少，表1共記錄到9次故障，傳統(tǒng)統(tǒng)計學方法可信度降低。

實際上，對于核電站大多機械部件，由于設計可靠度較高，現(xiàn)階段運行積累到的失效數(shù)據(jù)均面臨以上3個問題。

首先，為保留截止時未發(fā)生故障的時間信息，采用定時截尾試驗的格式對失效數(shù)據(jù)進行整理；其次，為考慮維修帶來的可靠度變化，引入可修復系統(tǒng)非齊次泊松過程（NHPP）模型［4］來處理數(shù)據(jù)的非獨立性問題；最后，針對失效樣本普遍較少的情況，采用目前較為成熟的貝葉斯方法進行處理［3］。進而綜合給出了一種解決核電站失效數(shù)據(jù)中上述問題的方法。

2 失效數(shù)據(jù)的處理

2.1 定時截尾試驗

定時截尾試驗是可靠性試驗的一種，失效信息可表述為 （n，r，t1，t2，…，tr，ts），其中：n為試驗總體個數(shù)；r為發(fā)生失效的個數(shù)；t1，t2，…，tr為次序排列的失效時間；ts為試驗截止時間。

由于核電站大多部件失效數(shù)據(jù)較少，采用定時截尾數(shù)據(jù)的格式可利用到截止時間信息，一定程度上擴大了樣本容量。

將核電站現(xiàn)場失效數(shù)據(jù)按照定時截尾試驗的格式來處理，需做以下近似：1）將每次失效作為單獨的1次記錄，認為這些數(shù)據(jù)服從同一壽命分布；2）假設每次故障起始時間相同，每次失效時間從零時刻開始到發(fā)生故障為止；3）合理選擇1個截止時間，使其包含所有故障記錄，同時認為運行時間大于它的記錄未發(fā)生失效。

以表1中數(shù)據(jù)為例，觀察其時間信息，取截止時間ts＝30 000h，此時有兩組數(shù)據(jù)（30 504、31 368）大于30 000h，認為未發(fā)生失效，這樣n＝11，r＝9。

同單獨故障間隔時間信息相比，在上述假設條件下，樣本大小由發(fā)生故障的9個擴充到11個（2個未發(fā)生失效），一定程度上利用原始信息擴大了樣本容量。

2.2 可修復系統(tǒng)與數(shù)據(jù)趨勢分析

某一部件運行過程中可能發(fā)生多次故障，進行維修或更換后部件的可靠度同初始相比會發(fā)生變化，故障間隔時間的分布不再獨立。這時不滿足修復如新的假設，通常采用的不可修復系統(tǒng)模型不再適用，需引入可修復系統(tǒng)模型進行處理。

常見的可修復系統(tǒng)模型包括：RP（Renewal Process）模型、HPP（Homogeneous Poisson Process）模型、BPP （Branching Poisson Process）模型、SRP（Superposed Renewal Process）模型和NHPP（Non－Homogeneous Poisson Process）模型。

D.M.Louit等［4］給出了一種采用數(shù)據(jù)趨勢分析方法選擇可修復系統(tǒng)模型的流程。針對表1中的數(shù)據(jù)進行趨勢分析，得到的總試驗時間曲線如圖1所示。橫坐標為第k次失效與總失效次數(shù)r的比值；用p（u）表示u時刻已發(fā)生失效的次數(shù)，則T（t）＝p（u）du為從0到t時刻總的試驗時間。圖1表明，失效率隨時間的增加而增加，進而可確定定子冷卻水泵機械密封失效數(shù)據(jù)服從NHPP模型。

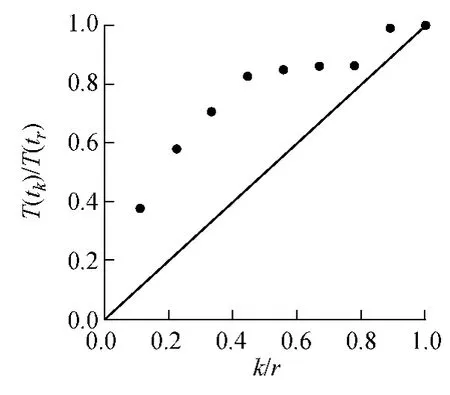
圖1 機械密封故障數(shù)據(jù)總試驗時間曲線Fig.1 Total time on test plot of mechanical seal failures

NHPP模型可用來描述設備的維修或替換未引起明顯的設備可靠性變化（圖2a）或發(fā)生單調變化（圖2b、c）的情況。定子冷卻水泵機械密封故障數(shù)據(jù)屬失效率增加（圖2b）的情況。

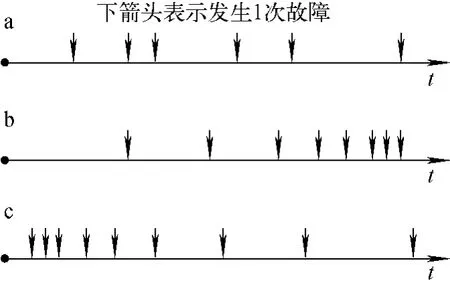
圖2 3種常見失效時間分布趨勢Fig.2 Three kinds of trends in time between failures

NHPP模型兩種常見的失效率表達方法是冪率失效率（也叫威布爾失效率）和對數(shù)線性失效率［4］。

冪率失效率的表達式為：

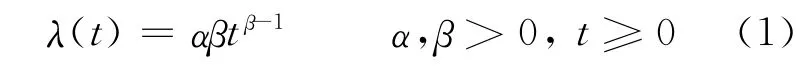
對數(shù)線性失效率的表達式為：

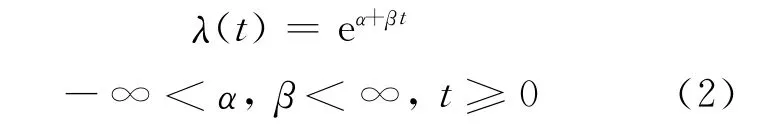
其中：α、β為待定值。

冪率失效率形式符合大多情況，其形式上等同于雙參數(shù)的威布爾分布的失效率，因此，下面的計算采用雙參數(shù)威布爾分布作為壽命分布來處理核電站失效數(shù)據(jù)。需指出的是，威布爾分布考慮了老化的影響，更符合機械部件發(fā)生老化退化的實際情況。

對于雙參數(shù)的威布爾分布，其故障概率密度函數(shù)為：

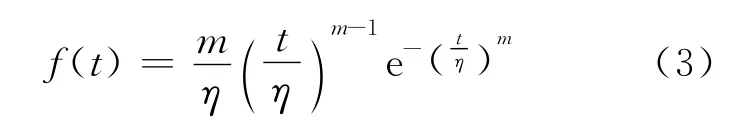
其中：m為形狀參數(shù)；η為尺度參數(shù)。

2.3 貝葉斯方法

由于核電站失效數(shù)據(jù)普遍較為缺乏，需考慮小樣本的處理方法。小樣本問題的特點是樣本容量較少，傳統(tǒng)的統(tǒng)計學方法不再適用。目前，國內外已發(fā)展許多解決小樣本數(shù)據(jù)問題的方法，如由金字塔式方法延伸出的矩擬合的方法、Huang等提出的用于解決多元正態(tài)分布的多重替代法、基于貝葉斯原理的延伸算法、基于計算機仿真的Bootstrap和蒙特卡羅方法等［6］。其中，貝葉斯方法是處理小樣本問題較為成熟的一種算法，可有效地綜合多種來源、多種形式的先驗信息，并根據(jù)電站運行情況進行數(shù)據(jù)更新。本工作選用貝葉斯方法來解決小樣本問題。

貝葉斯公式是貝葉斯理論的基礎，它可表示為：

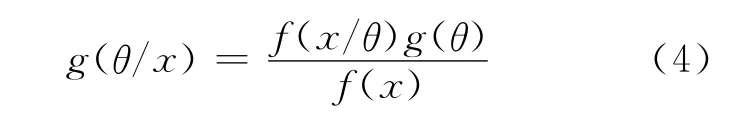
記X＝（x1，x2，…，xn）為樣本信息，θ為分布參數(shù)，上式中，f（x）＝∑f（x／θ）g（θ），為給定參數(shù)θ下xi的條件概率分布，稱為似然分布。g（θ／x）為給定x時參數(shù)θ的概率密度分布，即后驗分布。

對于服從威布爾分布失效數(shù)據(jù)，采用貝葉斯公式計算難以解析求解，考慮采用數(shù)值算法，計算過程如下。

1）根據(jù)失效數(shù)據(jù)和似然估計方程，得到Weibull分布參數(shù)的點估計和，參數(shù)極大似然估計的方程［5］為：

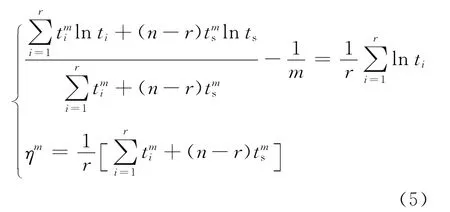
2）獲取先驗分布

對上步確定的威布爾分布參數(shù)和進行抽樣，產(chǎn)生M組樣本容量為n的Bootstrap再生樣本［6－7］。對M組樣本分別求解分布參數(shù)mj和ηj，然后假設mj和ηj相互獨立，得到m和η的離散先驗聯(lián)合概率密度的M×M矩陣：

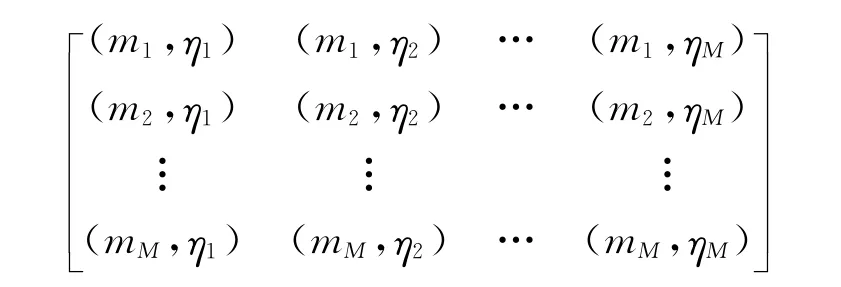
可得到，m＝mi，η＝ηj的概率為：

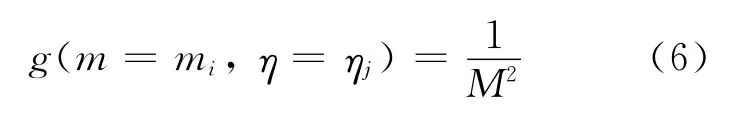
令其作為貝葉斯公式的先驗分布g（θ）。

3）根據(jù)貝葉斯公式進行計算

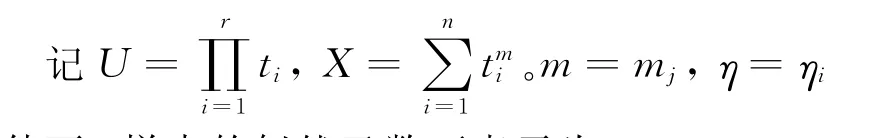
條件下，樣本的似然函數(shù)可表示為：

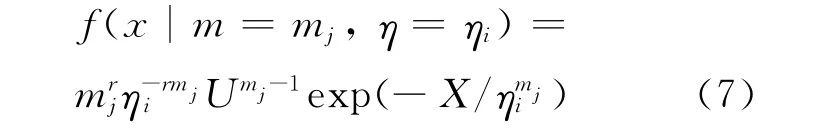
根據(jù)貝葉斯公式，經(jīng)現(xiàn)場失效信息修正后的m和η得離散的聯(lián)合驗后分布：

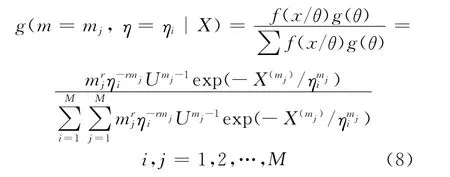
根據(jù)式（8）可得到關于m和η離散的聯(lián)合驗后分布，求其全概率可得到所求的部件壽命可靠度分布函數(shù)：

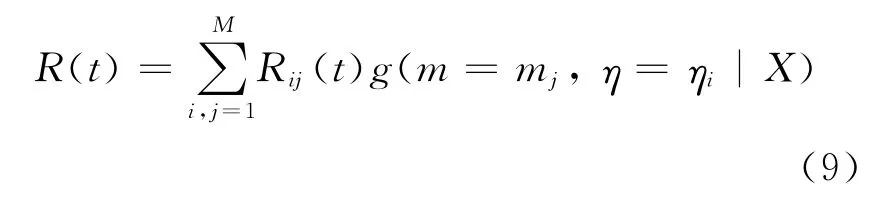
其中：Rij（t）＝

平均失效前的工作時間為：

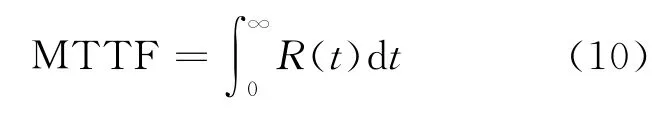
3 結果分析

定子冷卻水泵機械密封的失效數(shù)據(jù)為：n＝11，r＝9，ts＝30 000h。失效時間由小到大依次為：3 312、6 432、7 224、7 896、12 288、15 216、17 664、17 736、18 048h。

由于雙參數(shù)威布爾分布不存在共軛分布，原先假定的威布爾型壽命分布經(jīng)貝葉斯公式修正后不再是威布爾分布的形式。其解析表達式較為復雜，用可靠度隨時間的變化曲線表述，如圖3所示。同文獻［2］中結果的比較列于表2，MTTF可通過公式算出。

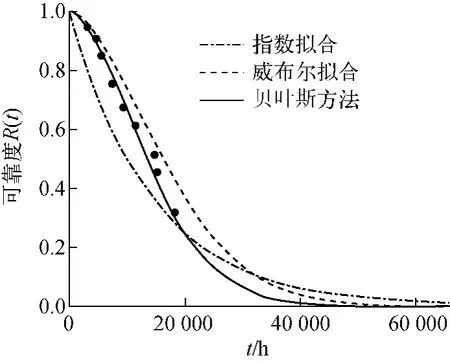
圖3 可靠度函數(shù)曲線Fig.3 Plot of reliability function

表2 同擬合結果的比較Table 2 Comparison with data fitting

采用指數(shù)分布擬合得到的平均故障前的工作時間明顯小于后兩種方法的結果，這是因為指數(shù)分布的模型未考慮失效率的增加，直接擬合得到的失效率為某種意義上的均值，這使得評估結果在初期較為保守，而在末期可能出現(xiàn)危險。同時貝葉斯方法可看作是對失效數(shù)據(jù)抽樣分布的修正，因此較直接采用威布爾分布擬合結果更接近電廠實際。同時本方法具有更好的適用性，可解決核電站數(shù)據(jù)處理過程中經(jīng)常面臨的樣本較少、不能直接擬合的問題。

4 結語

本文給出了一種實用的處理核電站失效數(shù)據(jù)的流程，可用于解決失效數(shù)據(jù)處理過程中面臨的分布不獨立、樣本容量少等問題。該方法通過將失效數(shù)據(jù)處理成定時截尾格式以保留部分檢查信息，以雙參數(shù)威布爾分布作為壽命模型從而避免了維修帶來的可靠度變化的影響，最后通過引入Bootstrap抽樣作為貝葉斯先驗分布來處理威布爾分布小樣本的問題，得到數(shù)值結果。

［1］SLITER G，CAREY J.Nuclear plant life cycle management implementation guide［R］.Palo Alto，USA：Electric Power Research Institute，1998.

［2］高緯光，劉井泉，劉鵬，等.發(fā)電機定子冷卻水泵可靠性數(shù)據(jù)處理及分析［J］.原子能科學技術，2009，43（9）：828－833.GAO Weiguang，LIU Jingquan，LIU Peng，et al.Processing and analysis of reliability data on stator cooling pump［J］.Atomic Energy Science and Technology，2009，43（9）：828－833（in Chinese）.

［3］周法清.核電廠概率安全評價［M］.上海：上海交通大學出版社，1996：146－153.

［4］LOUIT D M，PASCUAL R，JARDINE A K S.A practical procedure for the selection of time－to－failure models based on the assessment of trends in maintenance data［J］.Reliability Engineering and System Safety，2009，94（10）：1 618－1 628.

［5］金星，洪延姬，沈懷榮，等.可靠性數(shù)據(jù)計算及應用［M］.北京：國防工業(yè)出版社，2003：42－45.

［6］金星，洪延姬.系統(tǒng)可靠性評定方法［M］.北京：國防工業(yè)出版社，2004：27－77.

［7］段曉軍，王正明.小子樣下的Bootstrap方法［J］.彈道學報，2003（3）：1－5.DUAN Xiaojun，WANG Zhengming.Applicability of Bootstrap method in small sample case［J］.Journal of Ballistics，2003（3）：1－5（in Chinese）.