火球動態模型在溫壓炸藥熱毀傷效應評估中的應用＊

仲 倩，王伯良，黃 菊，房瑩瑩，惠君明

（南京理工大學化工學院，江蘇 南京 210094）

溫壓炸藥中一般添加鋁粉等高能添加劑以增加燃燒和爆炸效應，同時還添加部分高能炸藥以增強其起爆性能［1］，其熱輻射毀傷效應高于常規高能炸藥，因此溫壓炸藥的熱輻射毀傷效應評估研究具有極其重要的意義。

關于爆炸火球的熱輻射毀傷，前人做了很多研究與探討，何志光［2］分別用Baker模型和S.B.Dorofeev模型計算了二次引爆型云爆劑和一次引爆型云爆劑火球熱輻射的毀傷效應，認為Baker模型計算的熱劑量值顯著偏大，而S.B.Dorofeev模型計算結果比較合理。郭學永等［3］利用Baker模型分析了溫壓炸藥的熱輻射毀傷半徑。上述模型將爆炸火球簡單地假設為靜態，其體積、表面溫度和上升高度等表征參量瞬間達到最大并保持不變，但高速錄像測試結果表明溫壓炸藥在爆炸過程中，火球尺寸及上升高度等表征參量均是動態變化的，因此這些假設不利于準確評估爆炸火球的熱輻射毀傷效應。W.E.Martinsen［4］基于火球熱輻射基礎理論，建立了適合于過熱可燃液體瞬間燃燒的火球熱輻射動態模型，張董莉等［5］用Martinsen模型計算了沸騰液體蒸氣云爆炸火球的熱輻射毀傷后果，與靜態模型相比，該動態模型可體現火球的動態變化。但利用該動態模型在計算火球表面輻射參量時，將火球增長階段的表面輻射能看作定值，在計算大氣傳輸率參數時，忽略了CO2對傳輸系數的影響，而且火球直徑、火球高度及火球持續時間等參數表征是應用經驗、半經驗公式，參數的處理難以適用于具有復雜爆炸過程的火球，如具有后燃效應的溫壓炸藥火球。

本文中以Martinsen動態模型為基礎，對關鍵參數的選取進行分析和改進，結合紅外熱成像儀和高速攝像儀所測得的溫壓炸藥和TNT爆炸火球的表征參量，形成以實驗數據為基礎的火球熱輻射毀傷動態模型，并比較溫壓炸藥和TNT爆炸的火球熱輻射毀傷效應。

1 溫壓炸藥熱輻射動態模型

根據火球熱輻射理論［4］可知，目標接受的熱通量q（x，t）是火球表面熱輻射能E（t）、火球和目標之間的幾何視角系數F（x，t）及大氣傳輸率τ（x，t）的函數

火球對暴露目標所造成的毀傷效應是由熱輻射強度與目標暴露時間決定的，而火球持續時間很短，通常認為目標暴露時間等于火球持續時間。因此可以用熱輻射劑量

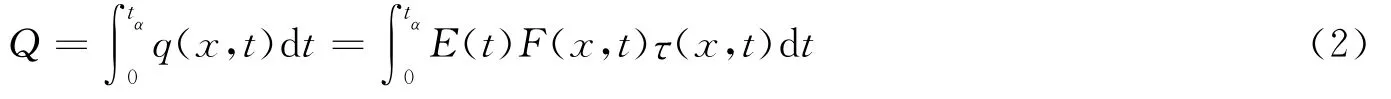
即熱通量q在火球持續時間tα內的積分來評估對暴露目標所造成的毀傷效應。

1.1 火球表面輻射能

文獻［4］中的火球表面輻射能計算公式是將火球表面輻射能看作與燃料質量、燃燒熱及燃燒熱輻射系數相關的定值，未反映出表面輻射能對溫度T的強烈依賴關系。因此，根據Stefan－Bolzmann方程，給出了火球表面輻射能與時間t的函數

式中：E為火球表面輻射能，W／m2；ε為火球表面比輻射率；σ為斯蒂芬·波爾茨曼常數，σ＝5.67×10－8W／（m2·K4）；T 為火球表面溫度，K。

1.2 幾何視角系數

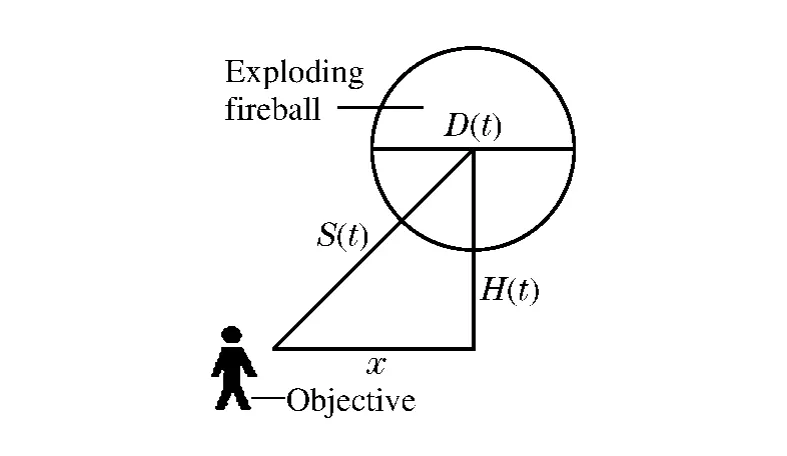
圖1 火球幾何視角Fig.1 Geometric perspective of fireball

由于目標所處位置不可能接受到輻射表面每個點的輻射能，因此需要引入幾何視角系數，即每單位面積上目標接受的輻射能與火球釋放的輻射能之比［5］。它不僅與火球大小、火球與目標的距離相關，還與火球與目標的相對方位相關。

假設目標在地面上，且與火球中心的連線垂直于火球表面，如圖1所示，則目標的最大幾何視角系數為

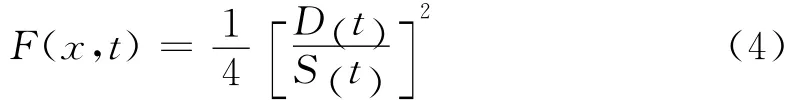
1.3 大氣傳輸率

大氣傳輸率τ（x，t）為考慮了空氣中水蒸氣和CO2等對熱輻射吸收后的傳輸系數，文獻［5］采用的計算公式為

式中：R為實驗時當地相對濕度；pV為對應環境溫度下水的飽和蒸氣壓，Pa。

用公式（5）計算時未考慮CO2對熱輻射的吸收影響，根據大氣中熱輻射的傳播和衰減規律，本文中采用文獻［6］中的大氣傳輸率公式

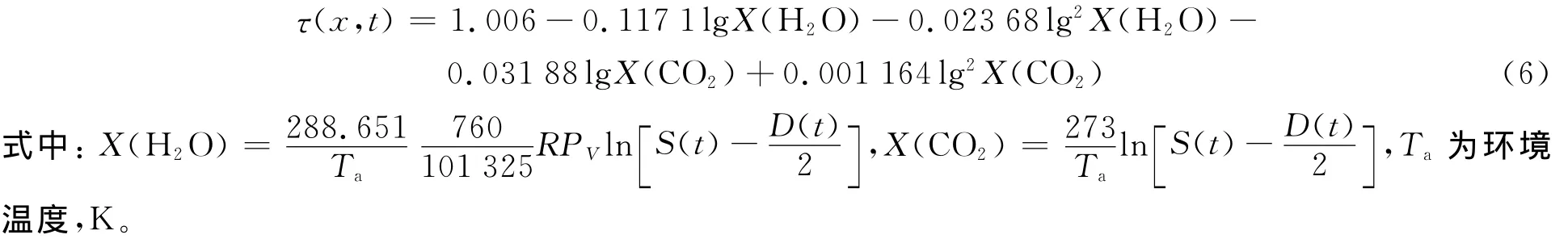
2 實 驗

2.1 實驗條件

實驗中采用30kg溫壓炸藥和同等質量的參比炸藥TNT，溫壓炸藥炸高1.33m，采用直立圓柱上下兩端起爆模式；TNT炸高1.33m，采用直立圓柱下端起爆方式。利用紅外熱成像儀和高速錄像儀，記錄熱輻射動態模型表征參數及實驗現象，儀器安放在距爆源130m的掩體內，鏡頭與爆心處于同一個水平面上，高速錄像儀掃描速度為2 000s－1，每種炸藥分別作2次平行實驗。

2.2 實驗結果

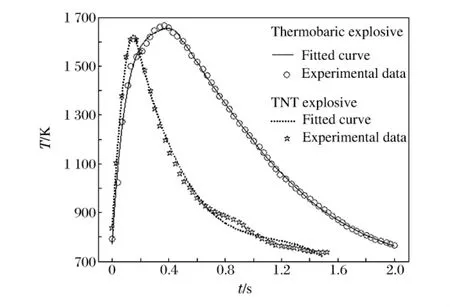
圖2 火球平均溫度擬合曲線Fig.2 Fitted curves of fireball’s average temperature

根據紅外熱成像和高速錄像儀的記錄結果，可得到火球溫度隨時間變化的數據，由于爆炸火球表面溫度分布不均勻，因此需取其表面溫度算術平均值，得到結果較為合理，平均溫度可采用紅外熱成像儀軟件處理得到，采用多項式擬合算法對實測數據進行分階段擬合，圖2為火球平均溫度實測數據與擬合曲線對比圖。

同理可對火球直徑和火球上升高度實測數據進行處理，表1列出了火球平均溫度T、火球直徑D及火球上升高度H 的擬合系數，并給出了各公式的適應范圍及擬合精度。表內擬合系數均是根據藥量為30kg時實測數據而通過多項式擬合算法獲得，擬合系數會根據藥量的不同而有所變化。

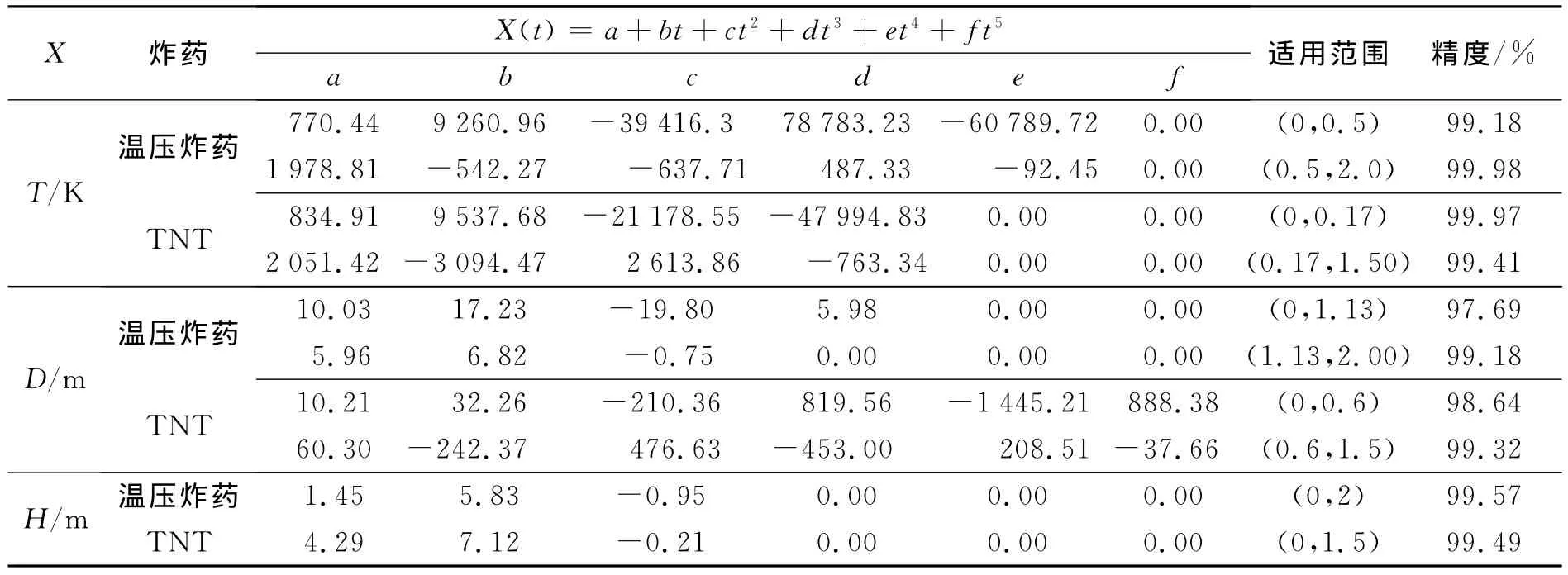
表1 溫壓炸藥和TNT的公式擬合系數Table1 Fitted coefficient of the thermobaric explosive and TNT

3 火球熱輻射動態模型計算結果

溫壓炸藥實驗環境溫度為24℃，相對濕度為48%。24℃時水的飽和蒸氣壓為2 987.87Pa。將擬合得到的火球平均溫度T（t）、火球直徑D（t）、火球上升高度 H（t）公式分別代入式（3）、（4）及（6），得到火球表面輻射能E（t）、幾何視角系數F（x，t）和大氣傳輸率τ（x，t）的函數，再將這些函數代入式（1）得到q（x，t），采用數值積分計算方法分3個積分段：0～0.50、0.50～1.13、1.13～2.00s對q（x，t）進行積分，得到不同距離x處的火球熱輻射劑量Qt，如表2所示。表中，Qt，1中考慮了CO2對熱輻射的吸收影響，Qt，2中沒有考慮CO2對熱輻射的吸收影響。

TNT的實驗環境溫度為28℃，相對濕度為38%。28℃時水的飽和蒸氣壓為3 780.17Pa。對得到的q（x，t）分3個積分段：0～0.17、0.17～0.60、0.60～1.50s進行積分，得到 TNT不同距離處的火球熱輻射劑量，如表2所示。為了討論CO2對熱輻射的吸收影響，應用式（5）的大氣傳輸率公式分別計算得到溫壓炸藥和TNT的熱劑量QT，如表2所示。表中，QT，1中考慮了CO2對熱輻射的吸收影響，QT，2中沒有考慮CO2對熱輻射的吸收影響。

由表2可知，不同距離處溫壓炸藥的熱輻射劑量可達TNT的3.6～4.8倍，溫壓炸藥具有顯著的熱輻射毀傷效應；CO2對火球熱輻射的計算結果存在一定的影響，最大差值百分比達到了29.26%，因此應用火球熱輻射動態模型計算炸藥的熱劑量時，應充分考慮CO2對熱輻射的吸收影響。

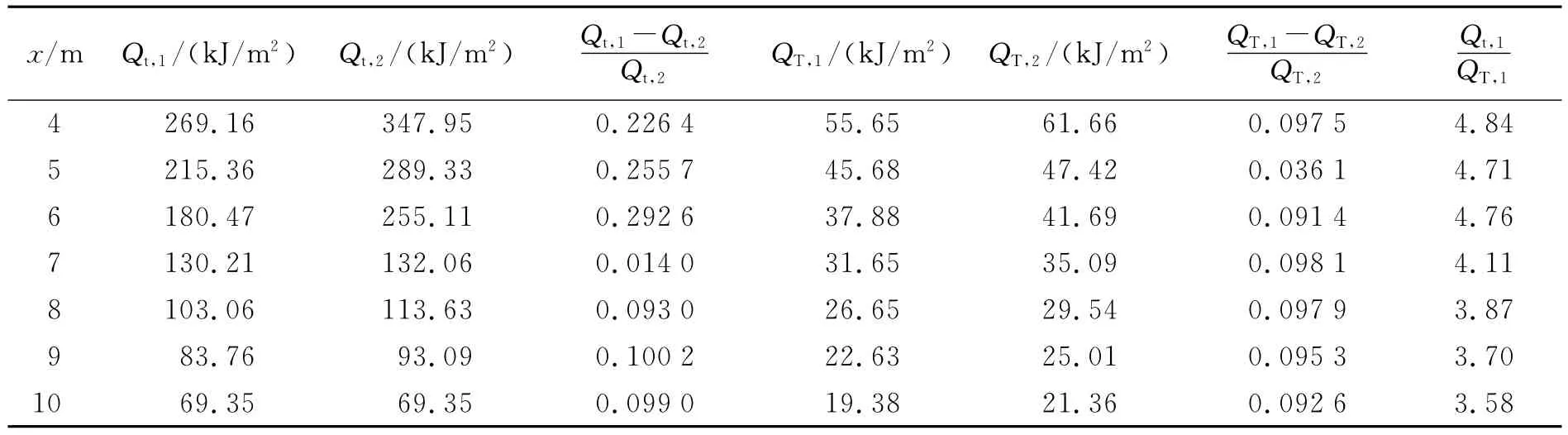
表2 溫壓炸藥和TNT的熱劑量計算結果Table2 Thermal dose of thermobaric explosive and TNT

4 與靜態模型計算結果對比分析

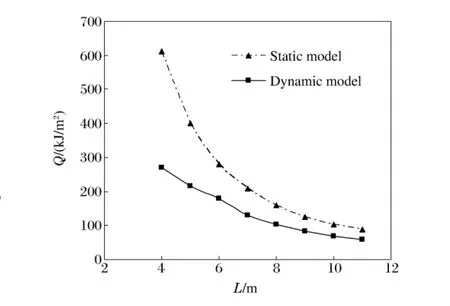
圖3 靜態模型與動態模型計算結果對比Fig.3 Comparison of results calculated with the static model and dynamic model

為了對動態模型和和靜態模型所得到的熱輻射毀傷效應加以比較，采用目前較常用的Baker靜態模型計算上述溫壓炸藥的熱輻射毀傷效應。用Baker模型計算熱劑量的公式為

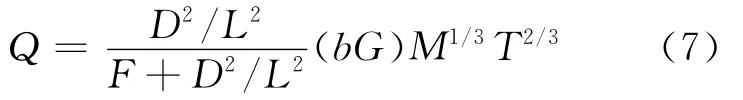
式中：T為火球溫度，K；D為火球直徑，m；L為目標到火球中心的距離，m；F為常量161.7；Q為熱劑量，J／m2；bG 為常量2.04×104；M 為火球消耗燃料質量，kg。

根據紅外熱成像儀和高速錄像測試結果可知：T＝2 547.85K，D＝12.16m，將測試數據帶入到式（7），即可求出靜態模型熱劑量值，計算結果如圖3所示。

從圖3可以看出，用Baker靜態模型公式計算的熱劑量顯著大于動態模型計算結果。因為靜態模型計算時，前提條件是假設火球直徑和火球溫度為常量，為測試過程獲得參量的最大值，未考慮火球上升高度和火球作用時間的影響。而實際爆炸過程中，火球各表征參量隨時間的變化不斷變化，均為時間函數。闞金玲［7］通過表面最大熱輻射量法，分析認為靜態模型計算結果顯著偏高的原因是火球直徑、體積及溫度等參數均在不停的變化，應用靜態模型進行毀傷效應評估不合理。因此利用動態模型計算得到的熱劑量和毀傷效應評估的結果更合理，理論上可以計算出一個相對接近實際的毀傷威力圈。

5 結 論

（1）以Martinsen動態模型為基礎，對火球表面輻射能和大氣傳輸率參數的選取和表征進行了分析和改進，形成了基于動態觀測實驗數據的火球動態模型。該模型更能體現出爆炸火球的動態特性；與靜態模型相比，動態模型可以模擬火球的動態變化過程，更合理地評估火球熱輻射毀傷效應。

（2）根據紅外熱成像儀所測數據，對溫壓炸藥火球表面的平均溫度、直徑及上升高度等表征參量進行了定量描述，以擬合公式方式揭示了其變化規律，建立了溫壓炸藥火球動態模型計算方法。

（3）火球動態模型計算結果表明，與TNT相比，溫壓炸藥的熱劑量可達TNT的3.6～4.8倍，具有較為明顯的高溫熱毀傷優勢，在封閉或半封閉空間，可作為主要的毀傷方式之一打擊目標。

［1］李秀麗，惠君明，張琳.光譜法遙感測定溫壓炸藥爆炸溫度的研究［J］.彈道學報，2008，20（2）：91－94.LI Xiu－li，HUI Jun－ming，ZHANG Lin.Explosion temperature measurement of thermobaric explosive by remote sensing spectroscopic method［J］.Journal of Ballistics，2008，20（2）：91－94.

［2］何志光.FAE爆炸火球熱輻射效應研究［D］.南京：南京理工大學，2004：29－37.

［3］郭學永，李斌，解立峰.溫壓藥劑的熱毀傷研究［J］.火炸藥學報，2008，31（1）：16－19.GUO Xue－yong，LI Bin，XIE Li－feng.Study on thermal damage of thermobaric explosive［J］.Chinese Journal of Explosive ＆ Propellants，2008，31（1）：16－19.

［4］Martinsen W E，Marx J D.An improved model for the prediction of radiant heat flux from fireball［C］∥Proceedings of CCPS International Conference and Workshop on Modeling Consequences of Accidental Releases of Hazardous Materials.San Francisco，California，1999：605－621.

［5］張董莉，劉茂，王煒，等.火球熱輻射后果計算動態模型的應用［J］.安全與環境學報，2007，7（4）：132－135.ZHANG Dong－li，LIU Mao，WANG Wei，et al.On the dynamic model application to the fireball radiation consequence calculation［J］.Journal of Safety and Environment，2007，7（4）：132－135.

［6］Phani K R.LNG fires：A review of experimental results，models and hazard prediction challenges［J］.Journal of Hazardous Materials，2007，140：444－464.

［7］闞金玲.液固復合云爆劑的爆炸和毀傷特性研究［D］.南京：南京理工大學，2008：43－47.