特征量對某交通流混沌實時判定系統的影響＊

盧 宇 張旭濤

（首都經濟貿易大學工商管理學院1） 北京 100070） （清華大學航天航空學院2） 北京 100084）（軍事交通學院裝備保障系3） 天津 300161）

交通流系統在一定條件下會出現混沌現象［1－2］.現有的混沌判定方法的一些局限性使其無法滿足交通流實時在線控制的要求.因此文獻［3］提出了一種混沌實時判定的新思路，文獻［4］通過從混沌時間序列演化軌跡中獲取的小段標量序列找出了混沌初始狀態，表明混沌與初始條件的對應關系雖然十分復雜，但是可以找到的.本文針對交通流混沌實時判定系統的特征提取模塊，選擇了3個常見的特征量，以交通流微觀仿真軟件產生的交通流為對象進行了實驗研究，討論了在其他實驗條件和步驟不變的情況下，不同的時間序列特征量（功率譜、小波包系數、小波包能量）對此判定系統判定結果的影響，從中得出較好反應時間序列特性的、有利于提高整個系統性能的特征量，更好地滿足交通流混沌實時判定的實時性、準確性的要求.

1 交通流混沌實時判定系統簡介

文獻［5］，構建了一個交通流混沌實時判定系統，其基本結構見圖1.

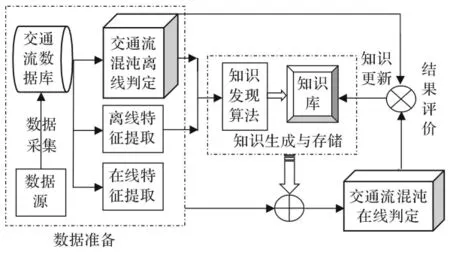
圖1 交通流混沌實時判定系統

2 所選特征量簡介

2.1 功率譜

1）計算時間序列的自相關函數 設交通流的時間序列｛xn：n＝1，2，…，N｝，xi為在ti時刻所得到的數據.其中t1，t2，…，tN分別為 Δt，2Δt，…，NΔt，Δt為時間序列的時間間隔.通常時間序列的自相關函數定義為

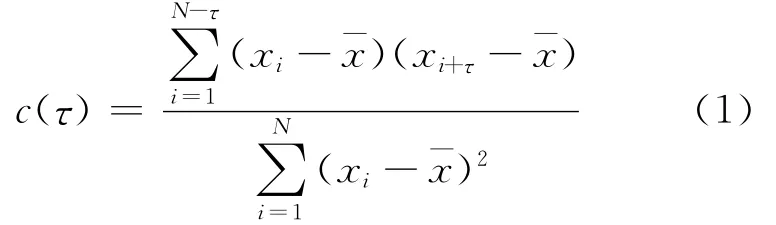
式中：τ∈（1，2，…，N－1）為時間延遲；xi＋τ為ti＋τ時刻所得到的數據的平均值.

2）對自相關函數進行Fourier變換 為提高計算速度，可采用快速Fourier變換，Fourier變換的結果為C（k），則

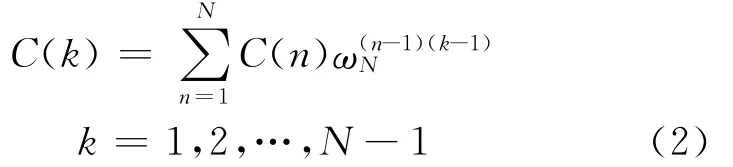
式中：ωN＝e（－2πi）／N，為了有效利用快速傅里葉算法，時間序列長度N應取2的冪次.

2.2 小波包分解

對時間序列進行3層的小波包分解（3層小波包分解樹結構示意圖見圖2，其中小波基函數取db1，Sij為小波包分解樹的節點，i為該節點的層次，j為節點在該層的位置），提取第3層由低頻到高頻的8個頻率成分的信號特征，得到相應的小波包分解系數.

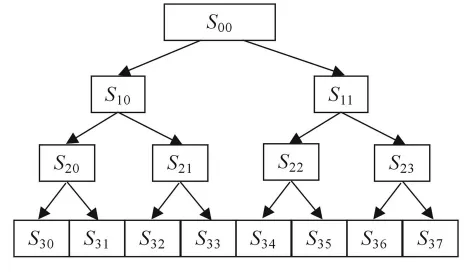
圖2 3層小波包分解樹的結構

2.3 小波包能量

設S3j（j＝0，1，2，3，4，5，6，7）對應的能量為

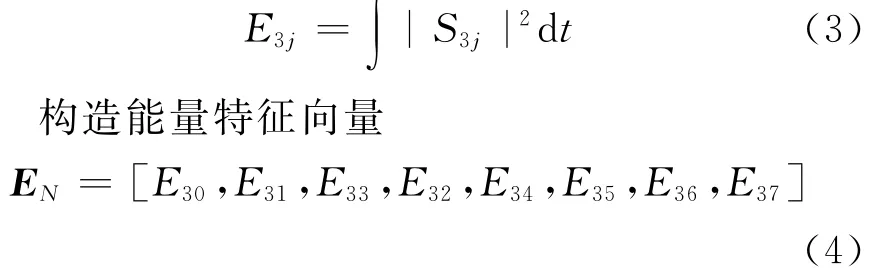
3 特征量對系統判定結果影響分析

筆者原來所在實驗室自主開發的交通流微觀仿真軟件不僅具有一般交通流微觀仿真軟件的基本功能，還有自身明顯的優點［6］.因此，由于篇幅所限，此處選擇3個常見的特征量，以此交通流微觀仿真軟件產生的交通流為對象進行實驗研究，討論在其他實驗條件和步驟不變的情況下，功率譜、小波包系數、小波包能量對此判定系統判定結果的影響.

另外，針對下面的實驗做幾點說明：（1）對于交通流混沌離線判定，由于Lyapunov指數法計算過程中主觀因素少，有確切的定量判據，判定結果準確，所以此處選用目前使用最廣泛的一種Jacobian方法——基于神經網絡估計器計算最大Lyapunov指數的方法［7］；（2）對于知識發現算法，由于神經網絡具有較強的非線性映射、學習、自適應等能力，是最常用的數據挖掘方法之一，因此采用最常用的神經網絡模型——BP神經網絡［8］，對知識進行生成、表達和記錄；（3）由于離散小波變換的原始時間序列的樣本點數都是2的整數次冪，加上要滿足交通流混沌實時判定的樣本量要求，再考慮到信息的損失與知識發現算法的速度與精度，下面實驗中都是選取32個樣本點的時間序列進行分析，關于時間序列樣本點數對系統判定結果的影響將另文討論.

3.1 基于功率譜的實驗研究

步驟1 應用上述交通流微觀仿真軟件，在仿真過程中采用仿真時間為2 000s，采樣間隔為1s進行采樣.通過隨機設置仿真時段、車型比例、司機類型，產生100組車頭時距的時間序列，每組時間 序 列 含 1 000 個 點，記 為 ｛xt｝t（＝N＋N1T）T（T ＝1 000，N ＝1，2，…，100）.

步驟2 利用前面選取的Jacobian方法計算每組時間序列的最大Lyapunov指數，判斷該時間序列是否具有混沌特性，若為混沌則該組時間序列對應的標記Q（N）＝1，否則Q（N）＝－1.這個結果被看作是該交通流時間序列是否存在混沌特性的真實結果.

步驟3 對每組交通流時間序列前32個點計算功率譜ωN作為特征向量，并以此作為“初始條件”.

步驟4 用BP神經網絡找出“初始條件”（功率譜向量ωN）和交通流時間序列是否存在混沌之間的對應關系.用前50組時間序列的特征向量（功率譜ωN）作為輸入，所對應組是否出現混沌的標記Q（N）作為網絡輸出，對網絡進行訓練.

步驟5 用后50組交通流時間序列的特征向量（功率譜ωN）作為訓練好的網絡的輸入進行混沌判定，判定結果與步驟2中計算的結果進行比較，觀察判定效果.

本實驗BP神經網絡取8個輸入節點和單輸出的三層網絡形式，按照步驟4所述進行訓練（設最大學習次數為2 000次，目標誤差為0.1），BP神經網絡的隱含層節點數由MATLAB函數自動獲得.其網絡訓練結果見圖3.

圖3 神經網絡訓練結果

由圖3可知BP神經網絡經過2 000次學習后，網絡已收斂，但未能達到訓練目標，均方誤差為0.819 749.因此以交通流時間序列的功率譜向量作為特征向量，應用于此交通流混沌實時判定系統，其判定結果的誤差很大.

3.2 基于小波包系數的實驗研究

步驟1 同3.1步驟1.

步驟2 同3.1步驟2.

步驟3 對每組交通流時間序列前32個點進行3層小波包分解（小波基函數取db1），提取第3層由低頻到高頻成分的32個小波包系數組成的向量θN作為特征向量，并以此作為“初始條件”.

步驟4 用BP神經網絡找出“初始條件”（小波包系數向量θN）和交通流時間序列是否存在混沌之間的對應關系.用前50組時間序列的特征向量（小波包系數θN）作為輸入，所對應組是否出現混沌的標記Q（N）作為網絡輸出，對網絡進行訓練.

步驟5 用后50組交通流時間序列的特征向量（小波包系數θN）作為訓練好的網絡的輸入進行混沌判定，判定結果與步驟2中計算的結果進行比較，觀察判定效果.

本實驗BP神經網絡取32個輸入節點和單輸出的三層網絡形式，按照步驟4所述進行訓練（設最大學習次數為5 000次，目標誤差為0.01），BP神經網絡的隱含層節點數由MATLAB函數自動獲得.其系統判定結果見表1.

表1 以小波包系數為特征量的系統判定結果

由表1可看出，以交通流時間序列的小波包系數作為特征向量，應用于此交通流混沌實時判定系統，其判定結果的誤差較大，結果并不很令人滿意.

3.3 基于小波包能量的實驗研究

步驟1 同3.1步驟1.

步驟2 同3.1步驟2.

步驟3 對每組交通流時間序列前32個點進行3層小波包分解（小波基函數取db1），提取第3層由低頻到高頻的8個頻率成分的信號特征，計算各時頻段的能量組成特征向量E（N），并以此作為“初始條件”.

步驟4 用BP神經網絡找出“初始條件”（小波包能量向量E（N））和交通流時間序列是否存在混沌之間的對應關系.用前50組時間序列的特征向量（小波包能量E（N））作為輸入，所對應組是否出現混沌的標記Q（N）作為網絡輸出，對網絡進行訓練.

步驟5 用后50組交通流時間序列的特征向量（小波包能量E（N））作為訓練好的網絡的輸入進行混沌判定，判定結果與步驟2中計算的結果進行比較，觀察判定效果.

本實驗BP神經網絡取8個輸入節點和單輸出的3層網絡形式，按照步驟4所述進行訓練（設最大學習次數為5 000次，目標誤差為0.01），BP神經網絡的隱含層節點數由MATLAB函數自動獲得.其系統判定結果見表2.

表2 以小波包能量為特征量的系統判定結果

由表2可見，以交通流時間序列的小波包能量作為特征向量，應用于此判定系統，其判定結果的誤差較小，結果能夠達到要求.

3.4 實驗結果分析

1）以功率譜作為特征量，在樣本量很小、噪聲大等一些因素的影響下，不能很好地反映出混沌與非混沌時間序列的明顯差異，因此不能很好的建立“初始條件”與是否出現混沌之間的對應關系，也就不能很好的應用此判定系統進行交通流混沌實時判定.

2）以小波包系數作為特征量，由于特征向量的維數較高（32個），以至于“初始條件”與是否出現混沌之間的對應關系過于復雜，根據神經網絡的知識可知，網絡的輸入維數過大會導致訓練樣本需求大、網絡難以收斂、結果誤差大，因此將小波包系數作為特征量應用于此判定系統進行交通流混沌實時判定，判定結果的誤差較大，不能令人滿意.

3）以小波包能量作為特征量，由于特征向量的維數較低（8個），可以減少訓練樣本需求量、提高網絡收斂速度和結果精確度，可以很好地建立“初始條件”與是否出現混沌之間的對應關系，因此將小波包能量作為特征量應用于此判定系統進行交通流混沌實時判定，判定結果的準確率較高，滿足實時判定交通流混沌的速度和精度要求.

4）對比功率譜、小波包系數、小波包能量這三個時間序列特征量，把基于小波包能量的特征提取應用于此交通流混沌實時判定系統，判定準確率最高，判定效果更好，可以較好地對微觀仿真交通流混沌進行判定，可以滿足交通流混沌實時判定的速度與準確性要求.

4 結束語

為分析功率譜、小波包系數、小波包能量對某交通流混沌實時判定系統判定結果的影響，以交通流微觀仿真軟件產生的交通流為對象進行了實驗研究.實驗結果表明：（1）特征量對該判定系統判定結果的影響較大；（2）在相同條件下，選用基于小波包能量的特征提取，該系統的判定結果的速度和準確性較高，判定效果更好；（3）此交通流混沌實時判定系統在正確地選取相關算法與參數的前提下，可以較好地進行交通流混沌實時判定，其所需樣本量少、計算速度快、判定準確率高，可以考慮應用于實際交通流系統中.

［1］王東山，賀國光.交通混沌研究綜述與展望［J］.土木工程學報，2003，36（1）：68－74.

［2］張 杰，賀國光.基于一維元胞自動機模型的交通流混沌研究［J］.武漢理工大學學報：交通科學與工程版，2009，33（1）：33－36.

［3］盧 宇，閻 利，張龍斌.某混沌實時判定系統中特征提取的原因分析［J］.河北工程大學學報：自然科學版，2009，26（3）：67－72.

［4］Liu F F，Xu D L，Wen G L.Tracing initial condition，historical evolutionary path and parameters of chaotic processes from a short segment of scarlar time series［J］.Chaos，Solition ＆ Fractals，2005，24：265－271.

［5］Johnson M，Habyarimana J.An operational test for distinguishing between complicated and chaotic behavior in deterministic systems［J］.Physica D：Nonlinear Phenomena，1998，116（3－4）：289－300.

［6］馬壽峰，賀國光，劉 豹.一種通用的城市道路交通流微觀仿真系統的研究［J］.系統工程學報，1998，34（4）：8－15.

［7］Mototsugu S，Oliver L.Nonparametric neural network estimation of Lyapunov exponents and a direct test for chaos［J］.Journal of Econometrics，2004，120（1）：1－33.

［8］飛思科技產品研發中心.神經網絡理論與 MATLAB7實現［M］.北京：電子工業出版社，2005.