市域鐵路與城市地鐵共站換乘模式分析＊

金 鍵 楊德明 明士軍

（西南交通大學交通運輸學院 成都 610031）

軌道交通不僅對于滿足城市間巨大的交通需求起著重要的作用，同時對都市群區域經濟結構的改變、城鎮體系的形成以及城市群產業結構的調整均有著重要的影響［1］.市域鐵路與城市地鐵作為軌道交通的重要形式，兩者之間的換乘模式和組織方式已成為交通流合理、有效轉換的關鍵［2］.通過兩者換乘站點模型的合理選取從而發揮兩者共同的優勢，使其相互之間取長補短，連接匹配.

1 共站換乘方式分析

市域鐵路與城市地鐵在很多方面存在大差異，比如制式、管理方面，然而同為軌道交通，兩者之間的換乘問題可以借鑒目前最為廣泛使用的同臺換乘［3］.同臺換乘是指乘客在同一站臺即可實現轉線換乘，即乘客只要走到車站站臺的另一邊就可以換乘另一條線路的列車［4］.換乘距離短、換乘方便，對兩端區間的影響小.本文重點研究平行換乘中的同臺換乘.根據軌道換乘站點的規模與客流之間的相互影響關系，將換乘方式分為單點、2點和多點共站三種類型.

1.1 單點共站換乘

單點共站換乘是由一個共站的換乘站連接市域鐵路與城市地鐵（見圖1）.軌道換乘站新建初期，由于客流沒有達到一定的規模，單點共站換乘即可滿足換乘節點的客流需求，建議在客流還沒有成熟時期市域鐵路與地鐵之間的換乘方式采用單點共站換乘.

圖1 單點共站換乘

1.2 2點共站換乘

2點共站換乘是設置兩個共站的換乘站連接市域鐵路路與城市地鐵路（見圖2）.決定2點共站模型與單點共站模型的關鍵性因素在于客流量需求的大小.體現在節點需求上面，節點的高峰客流的大小［5］.如果通道中高峰客流需求遠遠超過節點換乘的最大供給，即考慮采用2點共站模型.

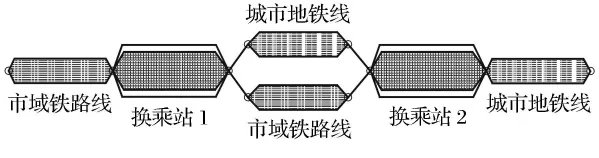
圖2 2點共站換乘

1.3 多點共站換乘

多點共站換乘是設置多個共站的換乘站連接市域鐵路路與城市地鐵路（見圖3）.當2點共站換乘方式不能滿足需求時，則考慮采用多點（3點或3點以上）共站換乘.采用多點共站換乘方式，其實質就是在同一通道中采取了軌道交通線路的共線運行［6］.這就需要有強大的客流需求作為支撐.

圖3 多點共站換乘

2 換乘模式影響因素分析

城市軌道交通系統在方向、時間、可達性、費用等方面均呈現出不均衡性，存在著單一或綜合性能的梯度變化，與此對應，換乘節點存在方向梯度、時間梯度、可達性梯度與費用梯度，換乘節點的梯度效應是決定換乘模式的關鍵影響因素.

2.1 節點方向梯度

城市用地布局的多種性、錯位分布以及開發強度決定了城市客運交通需求量的大小及其空間距離分布，即構建節點方向梯度.為保證出行時耗在可接受的范圍內，居民勢必要根據不同交通方式所能提供的運送速度和舒適度進行選擇.為了最大限度且最有效率地吸引周邊地區客流，單節點換乘站位置的確定顯得尤為重要.為此，將交通基礎信息利用圖論進行抽象，把單節點換乘站的位置抽象為節點網絡圖形中的形心.確定單節點共站模型形心從以下3個方面分析：（1）確定單節點換乘站所能覆蓋的范圍，即明確交通網絡圖形的形態、面積及范圍邊緣站點等基本特征；（2）確定方向客流，一旦線路走向確定，其客流流向可以通過調查得出；（3）確定客流密度，單節點換乘站應設置在客流密度較大的地區和集散點.

2.1.1 由范圍邊緣站確定交通網絡形心 假設交通網絡圖形為凸n邊形（先不考慮方向客流及客流密度的條件），確定此凸n邊形的形心公式［7］如下.

令凸n邊形的頂點（范圍邊緣站）坐標為（xi，yi），則

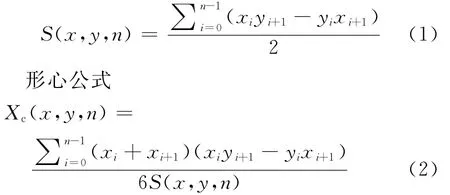
Yc（x，y，n）＝

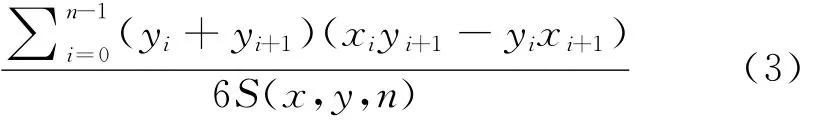
面積公式得出交通網絡的形心（Xc，Yc），即為市域鐵路與城市地鐵單點共站的位置所在.

2.1.2 由方向客流確定交通網絡形心 交通網絡中骨干通道上客流方向性極為明顯，市域鐵路和城市地鐵的線路走向必然積聚大量客流，方向性強的客運走廊的交點取為交通網絡的形心，見圖4.

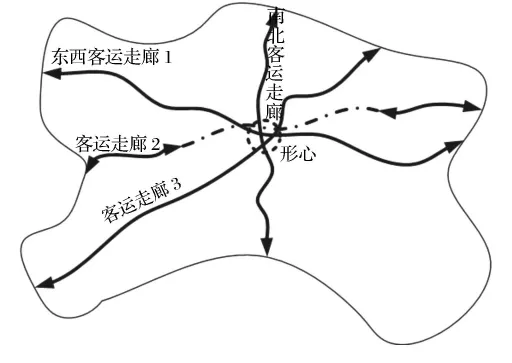
圖4 客運走廊分布確定形心

2.1.3 由客流密度確定交通網絡形心 客流的產生區域反映了軌道站點的吸引范圍的大小.軌道線路應沿著客流密度大的地區鋪設，同樣共站換乘節點應設置在客流密度較大的區域，以更方便的服務客流集散.

通過以上影響交通網絡形心重要因素的分析，構造節點方向梯度函數D（X）

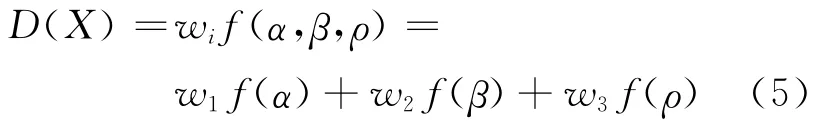
式中：α為范圍邊緣站；β為方向客流；ρ為客流密度；wi為各影響因素相對重要度.

根據影響交通網絡單節點位置因素的重要度對交通網絡形心進行修正，以最終確定交通網絡的形心，進而確定優化的單節點換乘站位置.

2.2 節點時間梯度

節點換乘站的時間梯度體現在客流隨時間變化而表現的極大不均衡性，具體表現在居民出行需求的日變化規律（客流以通勤（工作）與通學（上學）比例最高且早晚高峰出行強度大），周變化規律（工作日與周末客流需求的差異性），季節變化（寒暑期及黃金周客流突增）及突發性變化規律（重大體育賽事、大型公益活動、大型演唱會及博覽會等突發性的活動會吸引較大規模的客流））.

綜合以上影響因素分析，節點時間梯度T（X）

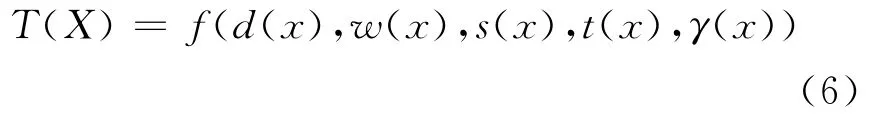
式中：d（x）為居民出行需求的日變化規律；w（x）為周變化規律；s（x）為季節性變化規律；t（x）為突發性變化規律；γ（x）為隨機影響因素.

2.3 節點可達性梯度

節點所覆蓋區域（吸引范圍）因相對距離的遠近和交通條件的不同，各節點換乘站的可達性當然會呈現出不均衡性，即節點可達性梯度.對交通來講，可達性是指利用一種特定的交通系統從某一給定區位到達活動地點的便利程度［8］，并有兩類度量方法：（1）無量綱，即將待度量的點與外部所有其他點之間可能的影響之和作為外界施加到該點上的總潛能；（2）有量綱，使用距離或時間來衡量可達性.本文采用第一種度量模型.

軌道交通客流的規模與軌道交通影響合理區域范圍的大小有著直接的聯系.節點可達性梯度與客流規模、發車頻率、站間距和速度有密切的關系.可達性隨著客流量增加而增加，隨著發車頻率的減小而增大；站間距和車輛速度越大，可達性就越大.

用以下的函數模型來分析節點可達性梯度R（X）

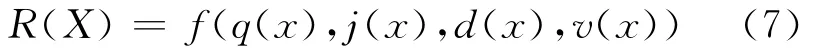
式中：q（x）為客流規模；j（x）為發車頻率；d（x）為站間距；v（x）為速度.

2.4 節點費用梯度

出行派生于社會活動，這說明居民的目的不僅僅在于單從出行本身獲得最大效用，而是要使出行與引起出行的某種活動一起達到最大效用，即出行過程中直接費用和非直接費用（如貨幣、時間等）以及出行方式所能到達的目的地帶來的效益（對出行方式的反饋評價）構成了節點的費用梯度.

為此，出行者出行前要對交通方式服務水平的7個指標進行衡量：安全性U1、經濟性U2、方便性U3、舒適性U4、快速性U5、準點率U6、出行帶來的效益U7，居民出行方式選擇的模糊評判因素集U為

式中：wi為第i個指標的權重；gi為評判某交通方式服務水平的因素集中各指標Ui的均值（i＝1，2，…，7）；Ui（X）為居民屬性服務效用評價函數［9］.

3 需求模型的構建

3.1 模型設定

影響共站節點需求的主要因素有節點方向梯度、節點時間梯度、節點可達性梯度和節點費用梯度等，將節點方向梯度等抽象加權得到節點梯度指數，此處用節點梯度指數來衡量節點梯度.據此可以建立以下方程

式中：S為共站節點需求量；D為節點方向梯度指數；T為節點時間梯度指數；R為節點可達性梯度指數；F為節點費用梯度指數；K，β為常數抑或表示各項彈性系數.

對上式兩邊取自然對數，為了反映共站節點實際需求與這些實際梯度指數變量之間的關系，須在模型右邊加上一個隨機干擾項ε，得

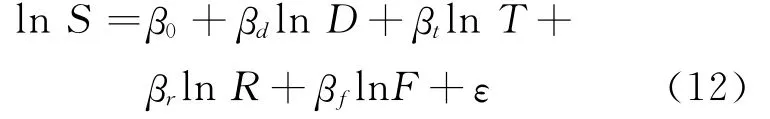
式中：β0＝ln K 為常數項.

式（12）即為共站節點需求的計量模型.對這種雙對數模型，應先將各變量進行對數化轉換成多元線性回歸模型，然后對該模型進行估算.即令ln S＝S′，ln D＝D′，ln T＝T′，ln R＝R′，ln F＝F′，則將雙對數模型式（7）變為多元線性回歸模型

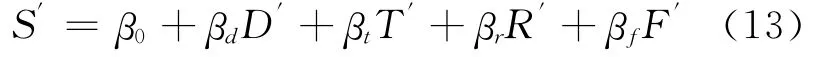
利用基礎數據對多元線性回歸模型進行標定［10］.

3.2 參數估計

根據專家評估對共站模型的節點方向梯度指數、時間梯度指數、可達性梯度指數和費用梯度指數進行數據抽象、量化、統計，得到節點梯度指數衡量標準見表1.

由表1的衡量標準以及3組經驗數據估計得到建模采用的相關統計數據及對數化處理后數據 見表2.

表1 節點梯度指數標準

表2 節點需求與梯度指數

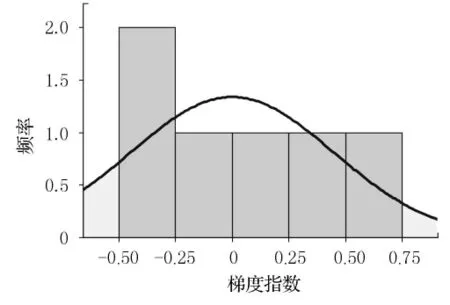
圖5 標準正態概率分布

表3 犀浦換乘站節點梯度指數

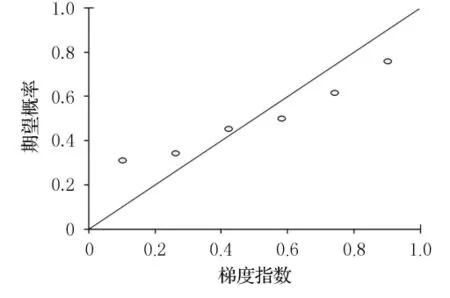
圖6 標準化殘差P－P分布

利用SPSS軟件進行多元線性回歸估算.因變量為共站節點需求（S），自變量選方向梯度指數（D）、時間梯度指數（T）、可達性梯度指數（R）和費用梯度指數（F）.觀察計算結果，對回歸系數多次檢驗得到較為理想的回歸模型

3.3 正態性檢驗

用SPSS軟件繪制標準化殘差P－P圖（正態概率分布圖），見圖5、圖6.

自變量節點方向梯度指數、時間梯度指數、可達性梯度指數和費用梯度指數對應的概率值P分別為0.342，0.401，0.2，0.057，在0.05的顯著性水平下，該模型能夠很好地通過回歸系數的顯著性檢驗以及總體性顯著檢驗.由圖6可知，各觀測點基本都分布在對角線附近（偏離很小），據此可以初步判斷殘差服從正態分布.

4 實例分析

本研究選取鐵二院規劃設計的成灌市域鐵路與成都地鐵二號線在犀浦換乘的換乘站為研究對象，分析此節點共站需求.根據此項目的相關調研數據分析，對此換乘站進行節點梯度指數抽象如表3所列.

利用回歸獲得的模型式（16），根據設定條件計算市域鐵路與城市地鐵共站節點的類型和需求量，這是研究共站需求模型的主要目的之一.由于未來軌道線網發展成熟程度和節點梯度估計的不同，共站節點需求量的預測也會有所不同［11］.

由回歸模型S＝8.523×10－3D－2.152T－1.866R0.357F－0.697，分別得到初期、近期和遠期的節點需求為0.95，1.74和2.73，取整即初期犀浦換乘站采用單點共站換乘，近期采用2點共站換乘，遠期采用三點共站換乘，這與近、遠期規劃相吻合，驗證了該模型的適用性.

5 結束語

市域鐵路與城市地鐵換乘模式主要取決于節點所在地區居民的出行強度和與相互間的協調程度（前者為節點的直接客流，后者為間接客流）.為此，本文根據城市軌道交通系統在方向、時間、可達性、費用等多種方面的不均衡性、差異性與層次性，劃分市域鐵路與城市地鐵的共站模式，構建共站節點需求模型，為軌道線網接駁、合理選擇節點共站模型和換乘方式等提供了依據.

［1］Nathaniel B S，Matthew E K.The effects of new public project s to expand urban rail transit ［J］.Journal of Public Economics，2000，77（2）：241－263.

［2］Christopher R B，Keith R I.The impact of rapid rail transit on economic development：the case of atlanta＇s MARTA［J］.Journal of Urban Economics，1997，42（2）：179－204.

［3］David R B，Keith R I.Identifying the impact s of rail transit stations on residential property values［J］.Journal of Urban Economics，2001，50（1）：1－25.

［4］Savage Ian.Scale economies in united states rail transit systems［J］.Transportation Research Part A ：Policy and Practice，1997 ，31（6）：459－473.

［5］金 鍵，張殿業，郭孜政.城市軌道交通合理規模機理及模型分析［J］.鐵道學報，2006，10（5）：17－20.

［6］秦文軍，梁成文.沈陽市快速軌道交通合理規模研究［J］.城市規劃，1999（9）：48－50.

［7］徐瑞華，杜世敏.市域軌道交通線路特點分析［J］.城市軌道交通研究，2005（1）：10－12.

［8］張國伍.交通運輸系統分析［M］，成都：西南交通大學出版社，2006.

［9］龐 浩.計量經濟學［M］.北京：科學出版社，2006.

［10］何曉群，劉文卿.應用回歸分析［M］.北京：中國人民大學出版社，2001.

［11］宇傳華.SPSS與統計分析［M］.北京：電子工業出版社，2007.